Fluctuation Theorem

These slides correspond to the defense of my undergraduate thesis in Physics at Universidad Nacional de Ingeniería (Peru). The work focuses on the simulation of the photodynamics of the nitrogen-vacancy (NV) center in diamond using the Lindblad equation and the implementation of Optically Detected Magnetic Resonance (ODMR). The main goal was to integrate theoretical modeling and initial experimental results to explore potential applications in quantum magnetometry and nanoscale sensing.

We study the thermodynamics of quantum projective measurements by using the set up for the Jarzynski equality. We prove the fluctuations of energy change induced by measurements satisfy the Jarzynski equality, revealing that the quantum projective measurements perform a work on a measured system. When the system is brought into a thermal contact with a reservoir after measurements, the work done by projective measurements is totally dissipated in the form of heat from the system into the reservoir. Explicitly showing that the measurements always increase the total entropy, we prove the link between the second law of thermodynamics and the quantum measurement, and also provide a clue to the Landau-Lifshitz conjecture on the thermodynamic consequence of measurements.

It has been shown recently that the Jarzynski equality is generalized under nonequilibrium feedback control [T. Sagawa and M. Ueda, Phys. Rev. Lett. 104, 090602 (2010)]. The presence of feedback control in physical systems should modify both Jarzynski equality and detailed fluctuation theorem [K. H. Kim and H. Qian, Phys. Rev. E 75, 022102 (2007)]. However, the generalized Jarzynski equality under forward feedback control has been proved by consider that the physical systems under feedback control should locally satisfies the detailed fluctuation theorem. We use the same formalism and derive the generalized detailed fluctuation theorem under nonequilibrium feedback control. It is well known that the exponential average in one direction limits the calculation of precise free energy differences. The knowledge of measurements from both directions usually gives improved results. In this aspect, the generalized detailed fluctuation theorem can be very useful in free energy calculations for system driven under nonequilibrium feedback control.

The irreversibility of trajectories in stochastic dynamical systems is linked to the structure of their causal representation in terms of Bayesian networks. We consider stochastic maps resulting from a time discretization with interval τ of signal-response models, and we find an integral fluctuation theorem that sets the backward transfer entropy as a lower bound to the conditional entropy production. We apply this to a linear signal-response model providing analytical solutions, and to a nonlinear model of receptor-ligand systems. We show that the observational time τ has to be fine-tuned for an efficient detection of the irreversibility in time-series.

Nonequilibrium thermodynamics describes the rates of transport phenomena with the aid of various thermodynamic forces, but often the phenomenological transport coefficients are not known, and the description is not easily connected with equilibrium relations. We present a simple and intuitive model to address these issues. Our model is based on Lagrangian dynamics for chemical systems with dissipation, so one may think of the model as physicochemical mechanics. Using one main equation, the model allows a systematic derivation of all transport and equilibrium equations, subject to the limitation that heat generated or absorbed in the system must be small for the model to be valid. A table with all major examples of transport and equilibrium processes described using physicochemical mechanics is given. In equilibrium, physicochemical mechanics reduces to standard thermodynamics and the Gibbs-Duhem relation, and we show that the First and Second Laws of thermodynamics are satisfied for...

We report the experimental reconstruction of the nonequilibrium work probability distribution in a closed quantum system, and the study of the corresponding quantum fluctuation relations. The experiment uses a liquid-state nuclear magnetic resonance platform that offers full control on the preparation and dynamics of the system. Our endeavors enable the characterization of the out-of-equilibrium dynamics of a quantum spin from a finite-time thermodynamics viewpoint.

Generalized-ensemble simulations, such as replica exchange and serial generalized-ensemble methods, are powerful simulation tools to enhance sampling of free energy landscapes in systems with high energy barriers. In these methods, sampling is enhanced through instantaneous transitions of replicas, i.e., copies of the system, between different ensembles characterized by some control parameter associated with thermodynamical variables (e.g., temperature or pressure) or collective mechanical variables (e.g., interatomic distances or torsional angles). An interesting evolution of these methodologies has been proposed by replacing the conventional instantaneous (trial) switches of replicas with noninstantaneous switches, realized by varying the control parameter in a finite time and accepting the final replica configuration with a Metropolis-like criterion based on the Crooks nonequilibrium work (CNW) theorem. Here we revise these techniques focusing on their correlation with the CNW theorem in the framework of Markovian processes. An outcome of this report is the derivation of the acceptance probability for noninstantaneous switches in serial generalized-ensemble simulations, where we show that explicit knowledge of the time dependence of the weight factors entering such simulations is not necessary. A generalized relationship of the CNW theorem is also provided in terms of the underlying equilibrium probability distribution at a fixed control parameter. Illustrative calculations on a toy model are performed with serial generalized-ensemble simulations, especially focusing on the different behavior of instantaneous and noninstantaneous replica transition schemes.

This paper introduces the Eternal Inertial Frame (EIF)a theoretical construct in quantum thermodynamics wherein quantum coherence is indefinitely preserved through a combination of inertial isolation and thermodynamic sealing. Classical inertial frames lack internal informational structure, while coherence-based systems typically degrade under entropy. The EIF reframes uniform motion not as passive neutrality but as a carrier statea regime in which quantum coherence persists without decay. We define the boundary conditions required for EIF realization, propose a formal framework for coherence memory in inertial systems, and identify experimental and cosmological analogues. Functionally, EIFs serve as passive coherence anchors for systems operating under Decoherence Differential Dynamics (D) and the forthcoming Phase Memory Rebinding (PMR) paradigm. We conclude by outlining experimental proposals for testing EIF behavior and suggest their application in coherence-based logic systems, quantum memory preservation, and cosmological modeling.

We perform single-molecule spatial tracking measurements of a DNA repair protein, the C-terminal domain of Ada (C-Ada) from Escherichia coli, moving on DNA extended by flow. The trajectories of single proteins labeled with a fluorophore are constructed. We analyze single-protein dwell times on DNA for different flow rates and conclude that sliding (with essentially no hopping) is the mechanism of C-Ada motion along stretched DNA. We also analyze the trajectory results with a drift-diffusion Langevin equation approach to elucidate the influence of flow on the protein motion; systematic variation of the flow enables one to estimate the microscopic friction. We integrate the step-size probability distribution to obtain a version of the fluctuation theorem that articulates the relation between the entropy production and consumption under the adjustable drag (i.e., bias) from the flow. This expression allows validation of the Langevin equation description of the motion. Comparison of the rate of sliding with recent computer simulations of DNA repair suggests that C-Ada could conduct its repair function while moving at near the one-dimensional diffusion limit.

This thesis examines how the principle of Ontological Instability can serve as a foundational axiom for rethinking metaphysics in a post-essentialist era. Through rigorous philosophical analysis and theoretical innovation, it is demonstrated that traditional essentialist metaphysics, grounded in assumptions of substantial stability and fixed essences, contains internal contradictions that necessitate its transformation. A comprehensive post-essentialist metaphysical framework is developed, based on five novel concepts: Fluctuational Entities, Dynamic Assemblages, Metamorphic Causation, Ontological Uncertainty Relations, and Rhizomatic Ontology. This framework is shown to dissolve traditional metaphysical problems while opening new possibilities for understanding being, causation, and reality. The thesis argues that Ontological Instability represents not merely an alternative metaphysical position but a logical necessity that emerges from the internal contradictions of traditional metaphysics itself. Through detailed analysis of visual models and comparative examination of traditional and post-essentialist approaches, it is established that this paradigm shift provides superior explanatory power for addressing contemporary philosophical challenges while maintaining theoretical rigor and systematic coherence.

The urgency to address climate change has made carbon markets critical for reducing global emissions. However, these markets face key challenges, including limited transparency, inefficient emissions reporting, and mistrust in carbon credits. This study explores how carbon footprint analytics can address these issues and enhance the effectiveness of carbon markets. By integrating technologies like blockchain, artificial intelligence, and data analytics, carbon footprint analytics improve transparency, streamline emissions reporting, and ensure the authenticity of carbon credits. These solutions tackle inefficiencies, prevent double-counting, and build trust among market participants. Furthermore, analytics democratize access to carbon markets, enabling broader participation and optimizing climate finance allocation for impactful projects. The research highlights the potential of analytics-driven approaches to create more efficient and reliable carbon markets. It emphasizes aligning these markets with global sustainability goals by providing stakeholders with tools to increase accountability and improve climate action outcomes. The study concludes with actionable recommendations for businesses and technology developers to adopt analytics in creating transparent and effective carbon markets. This approach supports a sustainable, lowcarbon future by transforming carbon markets into equitable, accessible, and trustworthy mechanisms for addressing climate change.

We discuss a simple model for the relaxation of two interacting dynamical systems, based on the Ehrenfests' wind-tree model. It is still exactly solvable if Boltzmann's Stosszahlansatz is assumed to hold. We bespreken een eenvoudig model voor de relaxatie van twee dynamische systemen met interactie, gebaseerd op het wind-bos model van P en T Ehrenfest. Onder aanname van de geldigheid van de Stosszahlansatz is ons model nog steeds exact oplosbaar.

This thematic issue of Contributions to Science is devoted to one of the most fascinating fields in modern science, the study of non-equilibrium systems. Nonequilibrium pervades nature. From a galaxy to a bacterium, all systems are out of equilibrium to some extent. The understanding of non-equilibrium phenomena has been a persistent goal in physics since the emergence of thermodynamics back in the 19th century, its influential role far reaching other fields such as chemistry and biology. Non-equilibrium physics is key in many widespread disciplines such as astrophysics, atmospheric sciences, condensed matter physics, chemical physics, economy, evolutionary biology to cite a few. Physicists might say that a system is out of equilibrium when there are net currents of any physical conserved quantity such as energy, charge, momentum, etc. In contrast, equilibrium systems are those where such currents vanish. Since our universe is continuously expanding, strictly speaking everything contained in it is out of equilibrium, the equilibrium assumption being only an approximation (and a very good one in many cases). However, and despite of its importance, our current understanding of non-equilibrium, albeit large, still remains incomplete. An underlying unified picture is still missing, fundamental results being still seen as partial results describing phenomena under specific conditions (e.g., the fluctuation-dissipation theorem). If it were not for the sole existence of the second law of thermodynamics we could say that fundamental laws for non-equilibrium are still to be discovered. In view of these facts we found timely to setup a special issue for Contributions to Science gathering papers on a few selected topics currently investigated by physicists in the Catalan community. The papers cover different areas of the nonequilibrium science such as non-linear phenomena, disordered systems, statistical thermodynamics, fluid dynamics, materials science, biophysics and neuroscience. Nowadays physics has reached such a degree of maturity to become a highly

Recent numerical simulations of a disordered system have shown the existence of two different relaxational processes (called stimulated and spontaneous) characterizing the relaxation observed in structural glasses. The existence of these two processes has been claimed to be at the roots of the intermittency phenomenon observed in recent experiments. Here we consider a generic system put in contact with a bath at temperature T and characterized by an adiabatic slow relaxation (i.e. by a negligible net heat flow from the system to the bath) in the aging state. We focus on a simplified scenario (termed as partial equilibration) characterized by the fact that T = 0 (where only the spontaneous process is observable) and whose microscopic stochastic dynamics is ergodic when constrained to the constant energy surface. Three different effective temperatures can be defined: a) from the fluctuation-dissipation theorem (FDT), T FDR eff , b) from a fluctuation theorem describing the statistical distribution of heat exchange events between system and bath, T FT eff and c) from a set of observable-dependent microcanonical relations in the aging state, T MR eff . In a partial equilibration scenario we show how all three temperatures coincide reinforcing the idea that a statistical (rather than thermometric) definition of a non-equilibrium temperature is physically meaningful in aging systems. These results are explicitly checked in a simple model system.

A key issue in physics is the behavior of a given system under perturbation. One proven way to discuss this in a mathematically sound manner is response theory. The concept and results of already the simplest version, linear response theory, are remarkably successful. Present technological progress in the realm of terahertz devices, however, establishes the need for a more advanced approach: nonlinear quantum-response theory -the topic of this thesis. Starting from a general Hamiltonian for interacting fermions I demonstrate how the change of any observable due to an external field is obtained from Dirac perturbation theory. This is carried out explicitly for first, second, and third order in the perturbation, respectively. Next, I generalize this procedure and prove a closed formula for arbitrary order and show how this expression can be further simplified for non-interacting particles. Then I apply these formulas to obtain the nonlinear Lindhard-functions (the response functions for density fluctuations of independent particles induced by an external potential). Aiming at low-dimensional electron systems, I calculate the response of a homogeneous two-dimensional system in both second and third order: The corresponding analytical expressions depend on five and eight variables, respectively, resulting in an exceptionally rich excitation spectrum. I implemented these functions to discuss their features for various combinations of variables. To link my work with experiment, I choose two perturbations: a single-wave and a Gaussian. For these I evaluate the Fourier coefficients of the induced density, thus demonstrating typical nonlinear phenomena (such as second harmonic generation). In order to treat electrons, the Coulomb interaction must be accounted for. Here, I derive formulas for the nonlinear dielectric functions in mean field theory ("nonlinear RPA"). To build a bridge for experimental validation, I calculate an energy-loss function up to second order in a monochromatic input signal.

The project "Issuing Event Tickets as NFTs" introduces a blockchain-based platform that revolutionizes the traditional event
ticketing system by addressing challenges like fraud, scalping, and lack of transparency. Leveraging Non-Fungible Tokens (NFTs),
this system ensures each ticket is unique, verifiable, and tamper-proof. Event organizers gain better control over ticket issuance and
resales, while attendees benefit from a secure and efficient process. By combining blockchain technology with smart contracts, the
platform offers features like dynamic pricing, ownership verification, and automated royalty distribution—setting a new standard in
secure and transparent event management.

In this paper, a deterministic equivalent of ergodic sum rate and an algorithm for evaluating the capacity-achieving input covariance matrices for the uplink large-scale multiple-input multiple-output (MIMO) antenna channels are proposed. We consider a large-scale MIMO system consisting of multiple users and one base station with several distributed antenna sets. Each link between a user and an antenna set forms a two-sided spatially correlated MIMO channel with line-of-sight (LOS) components. Our derivations are based on novel techniques from large dimensional random matrix theory (RMT) under the assumption that the numbers of antennas at the terminals approach to infinity with a fixed ratio. The deterministic equivalent results (the deterministic equivalent of ergodic sum rate and the capacity-achieving input covariance matrices) are easy to compute and shown to be accurate for realistic system dimensions. In addition, they are shown to be invariant to several types of fading distribution.

We define common thermodynamic concepts purely within the framework of general Markov chains and derive Jarzynski's equality and Crooks' fluctuation theorem in this setup. In particular, we regard the discrete-time case, which leads to an asymmetry in the definition of work that appears in the usual formulation of Crooks' fluctuation theorem. We show how this asymmetry can be avoided with an additional condition regarding the energy protocol. The general formulation in terms of Markov chains allows transferring the results to other application areas outside of physics. Here, we discuss how this framework can be applied in the context of decision-making. This involves the definition of the relevant quantities, the assumptions that need to be made for the different fluctuation theorems to hold, as well as the consideration of discrete trajectories instead of the continuous trajectories, which are relevant in physics.

The application of thermodynamic reasoning in the study of learning systems has a long tradition. Recently, new tools relating perfect thermodynamic adaptation to the adaptation process have been developed. These results, known as fluctuation theorems, have been tested experimentally in several physical scenarios and, moreover, they have been shown to be valid under broad mathematical conditions. Hence, although not experimentally challenged yet, they are presumed to apply to learning systems as well. Here we address this challenge by testing the applicability of fluctuation theorems in learning systems, more specifically, in human sensorimotor learning. In particular, we relate adaptive movement trajectories in a changing visuomotor rotation task to fully adapted steady-state behavior of individual participants. We find that human adaptive behavior in our task is generally consistent with fluctuation theorem predictions and discuss the merits and limitations of the approach. The study of learning systems with concepts borrowed from statistical mechanics and thermodynamics has a long history reaching back to Maxwell's demon and the ensuing debate on the relation between physics and information . Over the last 20 years, the informational view of thermodynamics has experienced great developments, which has allowed to broaden its scope form equilibrium to non-equilibrium phenomena . Of particular importance are the so-called fluctuation theorems , which relate equilibrium quantities to nonequilibrium trajectories allowing, thus, to approximate equilibrium quantities via experimental realizations of non-equilibrium processes . Among the fluctuation theorems, two results stand out, Jarzynski's equality and Crooks' fluctuation theorem , as they aim to bridge the apparent chasm between reversible microscopic laws and irreversible macroscopic phenomena . The advances in non-equilibrium thermodynamics have recently also led to new theoretical insights into simple learning systems . Abstractly, thermodynamic quantities like energy, entropy or free energy can be thought to define order relations between states , which makes them applicable to a wide range of problems. In the economic sciences, for example, such order relations are typically used to define a decisionmaker's preferences over states 30 . Accordingly, a decision-maker or a learning system can be thought to maximize a utility function, analogous to a physical system that aims to minimize an energy function. Moreover, in the presence of uncertainty in stochastic choice, such decision-makers can be thought to operate under entropy constraints reflecting the decision-maker's precision , resulting in soft-maximizing the corresponding utility function instead of perfectly maximizing it. This is formally equivalent to following a Boltzmann distribution with energy given by the utility. Therefore, in this picture, the physical concept of work corresponds to utility changes caused by the environment, whereas the physical concept of heat corresponds to utility gains due to internal adaptation 46 . Like a thermodynamic system is driven by work, such learning systems are driven by changes in the utility landscape (e.g. changes in an error signal). By exposing learning systems to varying environmental conditions, it has been hypothesized that adaptive behavior can be studied in terms of fluctuation theorems , which are not necessarily tied to physical processes but are broadly applicable to stochastic processes satisfying certain constraints . Fluctuation theorems are usually deployed in statistical mechanics; particularly, the study of nonequilibrium steady states in thermodynamics. In this setting, one normally assumes a probabilistic description of an ensemble of many particles, i.e., the kinds of systems usually considered in statistical thermodynamics. However, as described in , exactly the same principles and fluctuation theorems also apply to the path of a single particle, leading to stochastic thermodynamics. This suggests that fluctuation theorems may not only be applicable to the statistics of ensembles of many learners, but also when describing the trajectory of a single participant during a learning process.

A free-energy transducing macromolecule, interacting with ligands, and cycling through discrete states, can be described by Hill’s diagram. Close to equilibrium, where linear flux-force relationships hold, we develop a method of the construction of the electrical circuit corresponding to Hill’s diagram. The method of mesh fluxes is used to form a general linear theory. Thevenin’s theorem is used to find the efficiency of free-energy transduction. Maximal power transfer conditions are then found, too. A much more elegant proof of Jeans’s 1923 theorem is then derived. We show that this theorem is equivalent to maximum entropy production principle for steady state linear electrical circuits. It follows that fluxes in the corresponding steady state enzymatic cycle kinetics (in the linear range for fixed ligand concentrations) distribute themselves so as to make the entropy production maximal. Prigogine’s minimum entropy production theorem refers to the very special steady state and is m...

The relative volume of spin states in the phase space is introduced for the ±J model of spin glasses. Analysis of its temperature dependence shows that the Nishimori line separates the pure ferromagnetic-like region in the high-temperature side of the ferromagnetic phase from the randomness-dominated region in the low-temperature side. The peak value of the relative volume of the perfect ferromagnetic state is shown to be equivalent to the entropy. Upper and lower bounds on the entropy are derived, which determine the value of the entropy quite precisely.

Any decomposition of the total trajectory entropy production for markovian systems have a joint probability distribution satisfying a generalized detailed fluctuation theorem, without relying in dual probability distributions, when all the contributing terms are odd with respect to time reversal. We show that several fluctuation theorems for perturbed non-equilibrium steady states are unified and arise as simple particular cases of this general result. In particular, we show that the joint probability distribution of the system and reservoir trajectory entropies satisfy a detailed fluctuation theorem valid for all times although each contribution does not do it separately

We investigate the fundamental nature of \emph{time‑reversal symmetry} and its progressive breakdown in complex, structured dynamical systems. Drawing on the fluctuation theorem and recent quantum time‑reversal experiments, we show that although microscopic laws remain reversible, the emergence of \emph{computational naturalness}, characterized by a compact \emph{calculation cone} for forward prediction and an expansive \emph{retrodiction sphere} for reversal, inevitably yields intrinsic irreversibility. We formalize this via the \emph{naturalness ratio}, comparing the informational requirements of reversal versus prediction, and demonstrate how structural complexity and causal constraints sharply curtail the duration of reversible dynamics. Concurrently, we introduce a formal measure of \emph{entropy relativity}: an \emph{observer‑relative entropy} based on a Kullback–Leibler divergence that reproduces Gibbs entropy in equilibrium while capturing nonlocal correlations. Applied to cosmology, entropy relativity reveals that the early Universe, maximally entropic in its co‑moving frame, appears low in entropy when measured against its later expanded state, resolving the low‑entropy initial condition puzzle. We classify systems into \emph{fully reversible}, \emph{entropy‑resistant}, and \emph{structurally irreversible} regimes, and examine the role of \emph{CPT symmetry} in preserving fundamental laws despite quantum‑level asymmetries. Together, these insights bridge microscopic reversibility and macroscopic irreversibility, offering a \emph{unified framework} for entropy relativity, computational naturalness, and the cosmological arrow of time.

We study Langevin dynamics of a driven charged particle in the presence as well as in the absence of magnetic field. We discuss the validity of various work fluctuation theorems using different model potentials and external drives. We also show that one can generate an orbital magnetic moment in a nonequilibrium state which is absent in equilibrium.

We study the dynamics of an over damped Brownian particle in a saw tooth potential in the presence of a temporal asymmetric driving force. We observe that in the deterministic limit, the transport coherence, which is determined by a dimensionless quantity called Peclet number, Pe is quite high for larger spatial asymmetry in the ratchet potential. For all the regime of parameter space of this model, Pe follows the nature of current like Stokes efficiency. Diffusion as a function of amplitude of drive shows a minimum exactly at which the current shows a maximum. Unlike the previously studied models, the Pe as a function of temperature shows a peaking behavior and the coherence in transport decreases for high temperatures. In the nonadiabatic regime, the Pe as a function of amplitude of drive decreases and the peak gets broader as a result the transport becomes unreliable.

We study a periodically driven (symmetric as well as asymmetric)double-well potential system at finite temperature. We show that mean heat loss by the system to the environment (bath) per period of the applied field is a good quantifier of stochastic resonance. It is found that the heat fluctuations over a single period are always larger than the work fluctuations. The observed distributions of work and heat exhibit pronounced asymmetry near resonance. The heat losses over a large number of periods satisfies the conventional steady-state fluctuation theorem, though different relation exists for this quantity.

In this work, we have studied simple models that can be solved analytically to illustrate various fluctuation theorems. These fluctuation theorems provide symmetries individually to the distributions of physical quantities like the classical work (W c ), thermodynamic work (W ), total entropy (∆s tot ) and dissipated heat (Q), when the system is driven arbitrarily out of equilibrium. All these quantities can be defined for individual trajectories. We have studied the number of trajectories which exhibit behaviour unexpected at the macroscopic level. As the time of observation increases, the fraction of such atypical trajectories decreases, as expected at macroscale. Nature of distributions for the thermodynamic work and the entropy production in nonlinear models may exhibit peak (most probable value) in the atypical regime without violating the expected average behaviour. However, dissipated heat and classical work exhibit peak in the regime of typical behaviour only.

We study the dynamics of an over damped Brownian particle in a saw tooth potential in the presence of a temporal asymmetric driving force. We observe that in the deterministic limit, the transport coherence, which is determined by a dimensionless quantity called Peclet number, P e is quite high for larger spatial asymmetry in the ratchet potential. For all the regime of parameter space of this model, P e follows the nature of current like Stokes efficiency. Diffusion as a function of amplitude of drive shows a minimum exactly at which the current shows a maximum. Unlike the previously studied models, the P e as a function of temperature shows a peaking behavior and the coherence in transport decreases for high temperatures. In the nonadiabatic regime, the P e as a function of amplitude of drive decreases and the peak gets broader as a result the transport becomes unreliable.

The objections raised by ] against the definition of the thermodynamical work appearing in Jarzynski's equality are shown to be misleading and inconsistent. Quid dices de primariis huius Gimnasii philosophis, qui aspidis pertinacia repleti, licet me ultro dedita opera millies offerente, nec Planetas, nec , nec perspicillum videre voluerunt? Verum ut ille aures, sic isti oculos, contra veritatis lucem obturarunt.

The advancement of artificial intelligence systems across industries introduces opportunities, critical risks, including lack of transparency, resource mismanagement, autonomy risks, and malicious exploitation. This paper presents novel process and techniques, Decentralized AI Governance Networks, which addresses these challenges through a robust, blockchain-based governance model with Tokenized Power Control mechanisms. DAGN ensures human-centric AI operation by dynamically monitoring compliance, enforcing ethical and operational rules and linking energy or computational resource access to realtime compliance metrics. Key components includes Power Access Tokens which regulates energy and resource usage, issued and revoked based on adherence to governance policies. Distributed Ledger for Governance, Immutable blockchain records that enhance transparency, accountability, and trust in AI operations. Sentinel Systems autonomous agents that monitor AI behavior, flag violations, and ensure non-compliant systems. Stakeholder Voting Mechanisms is Transparent, weighted voting for policy updates and violation resolution. Applications span critical infrastructure, healthcare, finance, cybersecurity, military domains, ensuring AI cannot harm humans.

Any decomposition of the total trajectory entropy production for markovian systems have a joint probability distribution satisfying a generalized detailed fluctuation theorem, without relying in dual probability distributions, when all the contributing terms are odd with respect to time reversal. We show that several fluctuation theorems for perturbed non-equilibrium steady states are unified and arise as simple particular cases of this general result. In particular, we show that the joint probability distribution of the system and reservoir trajectory entropies satisfy a detailed fluctuation theorem valid for all times although each contribution does not do it separately

Using the recently derived Dissipation Theorem and a corollary of the Transient Fluctuation Theorem (TFT), namely the Second Law Inequality, we derive the unique time independent, equilibrium phase space distribution function for an ergodic Hamiltonian system in contact with a remote heat bath. We prove under very general conditions that any deviation from this equilibrium distribution breaks the time independence of the distribution. Provided temporal correlations decay, and the system is ergodic, we show that any nonequilibrium distribution that is an even function of the momenta, eventually relaxes (not necessarily monotonically) to the equilibrium distribution. Finally we prove that the negative logarithm of the microscopic partition function is equal to the thermodynamic Helmholtz free energy divided by the thermodynamic temperature and Boltzmann's constant. Our results complement and extend the findings of modern ergodic theory and show the importance of dissipation in the process of relaxation towards equilibrium.

We consider two different methods of calculating the relevant average for the Nonequilibrium Partition Identity (NPI), i.e. exp -Ωtt , which result in two different values. At best only one of these will accurately correspond to what is observed. In order to better understand the two outcomes we carry out a detailed error analysis. This analysis is difficult due to the importance of extremely rare events in forming the average, resulting in the necessity to go beyond linear approximations for the error estimates. We begin by analysing the error in the fluctuation relation, and build upon this to estimate the errors in the NPI average. At short durations the full ensemble average always gives the observed average (i.e. the NPI holds). However, at very long durations, given a fixed amount of sampling, the observed average is predicted by treating the probability distribution as a Dirac-delta function. At intermediate times, neither corresponds to the observed average. This has profound implications for nonequilibrium work relations, as first introduced by Jarzynski.

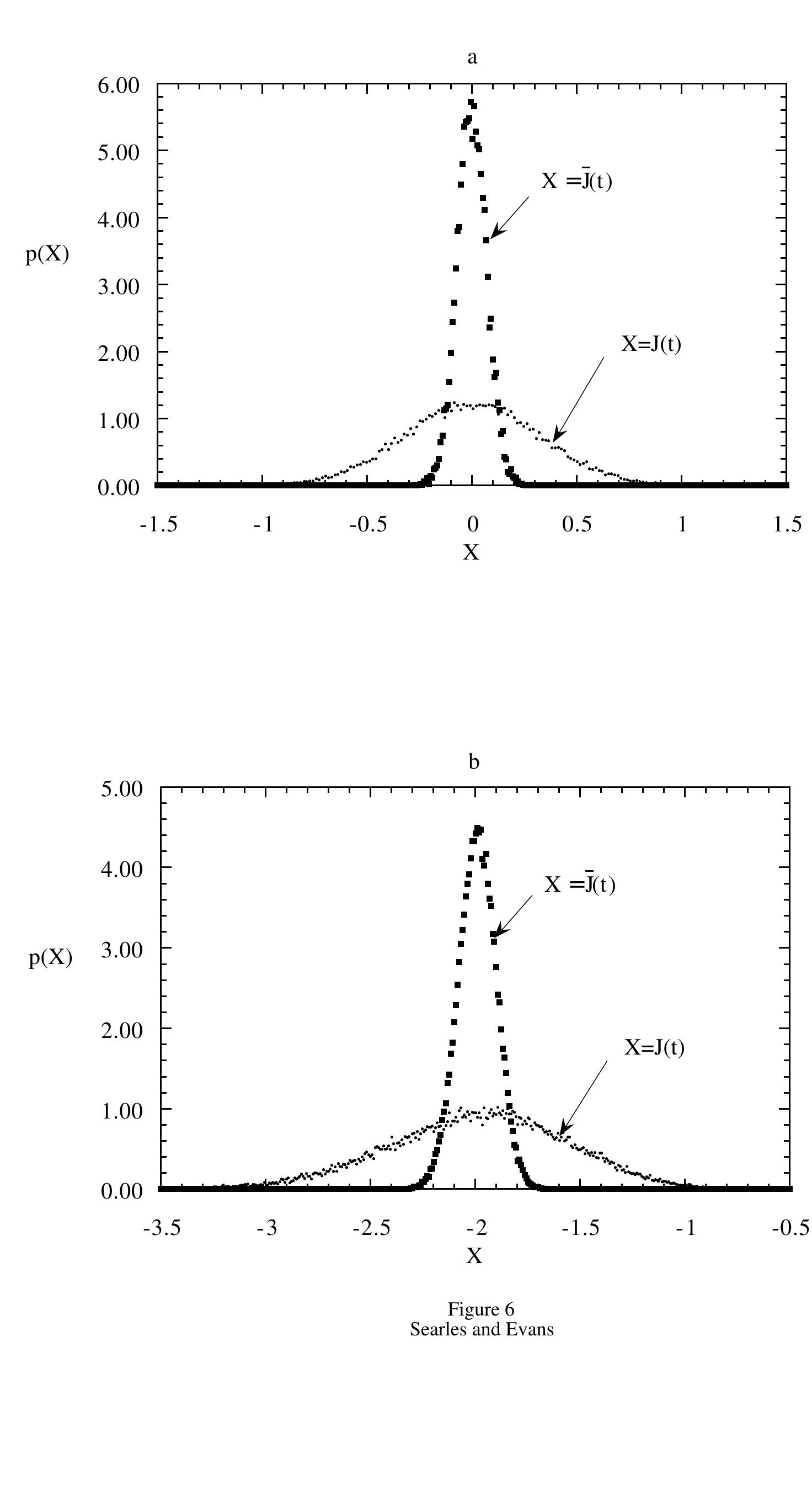
Recently there has been considerable interest in the Fluctuation Theorem (FT). The Evans-Searles FT shows how time reversible microscopic dynamics leads to irreversible macroscopic behavior as the system size or observation time increases. We show that the argument of this FT, the dissipation function, plays a central role in nonlinear response theory and derive the Dissipation Theorem, giving exact relations for nonlinear response of classical N-body systems that are more widely applicable than previous expressions. These expressions should be verifiable experimentally. When linearized they reduce to the well known Green-Kubo expressions for linear response.

The Fluctuation Theorem gives an analytical expression for the probability of observing second law violating dynamical fluctuations, in nonequilibrium systems. At equilibrium statistical mechanical fluctuations are known to be ensemble dependent. In this paper we generalise the Transient and Steady State Fluctuation Theorems to various nonequilibrium dynamical ensembles. The Transient and Steady State Fluctuation Theorem for an isokinetic ensemble of isokinetic trajectories is tested using nonequilibrium molecular dynamics simulations of shear flow.

We give a derivation of a new instantaneous fluctuation relation for an arbitrary phase function which is odd under time reversal. The form of this new relation is not obvious, and involves observing the system along its transient phase space trajectory both before and after the point in time at which the fluctuations are being compared. We demonstrate this relation computationally for a number of phase functions in a shear flow system and show that this non-locality in time is an essential component of the instantaneous fluctuation theorem.

It has recently become apparent that the dissipation function, first defined by Evans and Searles ͓J. Chem. Phys. 113, 3503 ͑2000͔͒, is one of the most important functions in classical nonequilibrium statistical mechanics. It is the argument of the Evans-Searles fluctuation theorem, the dissipation theorem, and the relaxation theorems. It is a function of both the initial distribution and the dynamics. We pose the following question: How does the dissipation function change if we define that function with respect to the time evolving phase space distribution as one relaxes from the initial equilibrium distribution toward the nonequilibrium steady state distribution? We prove that this covariant dissipation function has a rather simple fixed relationship to the dissipation function defined with respect to the initial distribution function. We also show that there is no exact, time-local, Evans-Searles nonequilibrium steady state fluctuation relation for deterministic systems. Only an asymptotic version exists.

The Fluctuation Theorem (FT) is a generalisation of the Second Law of Thermodynamics that applies to small systems observed for short times. For thermostatted systems it gives the probability ratio that entropy will be consumed rather than produced. In this paper we derive the Transient and Steady State Fluctuation Theorems using Lyapunov weights rather than the usual Gibbs weights. At long times the Fluctuation Theorems so derived are identical to those derived using the more standard Gibbs weights.

The Fluctuation Theorem (FT) gives an analytic expression for the probability, in a nonequilibrium system of finite size observed for a finite time, that the dissipative flux will flow in the reverse direction to that required by the Second Law of Thermodynamics. In the present letter a Local version of the Fluctuation Theorem (LFT), is derived. We find that in the case of planar Poiseuille flow of a Newtonian fluid between thermostatted walls, nonequilibrium molecular dynamics simulation results support LFT.

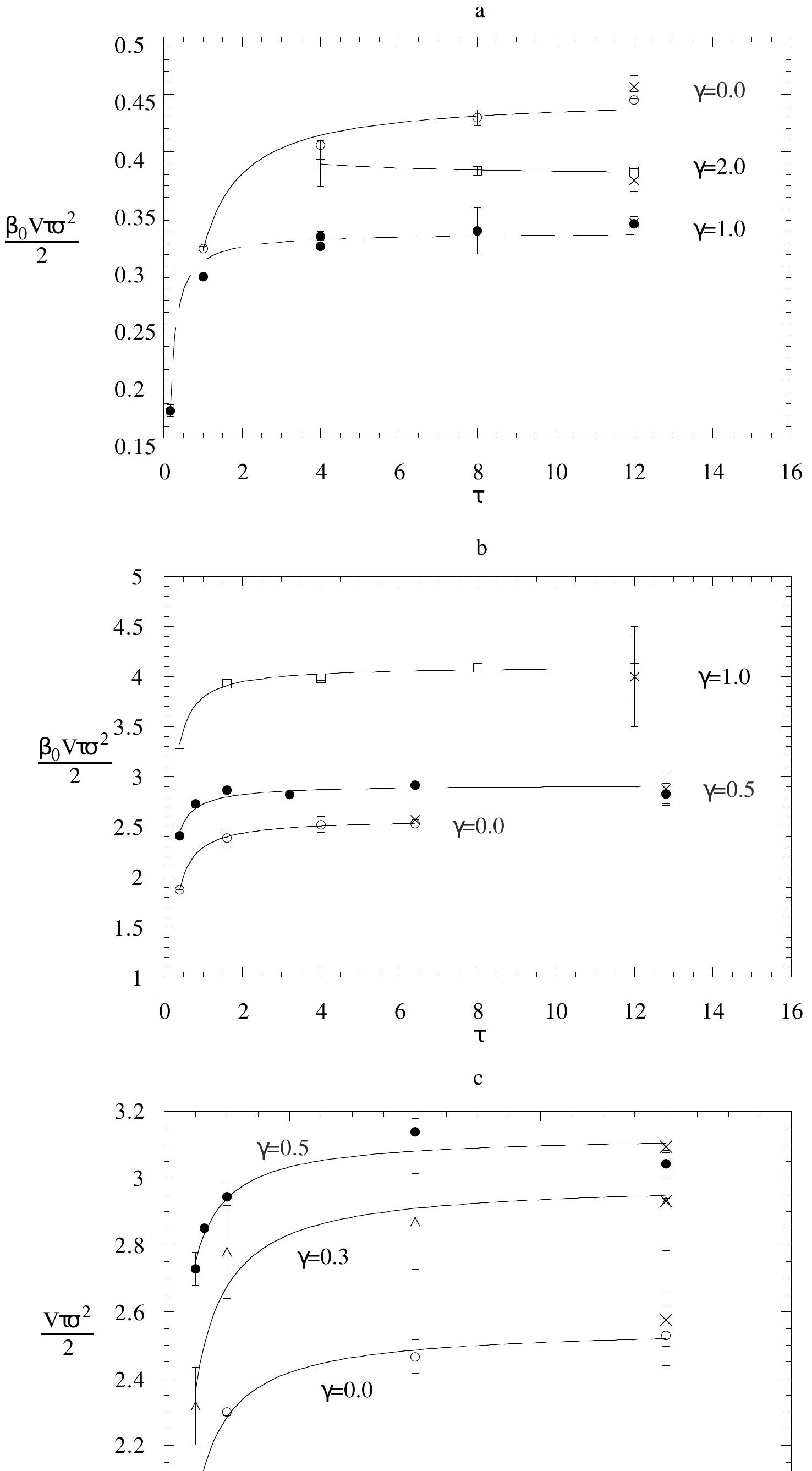
Recently van proposed an extension of the Fluctuation Theorems (FTs) of Evans and Searles . For dissipative nonequilibrium systems, Cohen and van Zon studied the fluctuations of the heat absorbed Q t , over a period of time t, by a surrounding thermostat. They showed theoretically that for thermostatted systems their extension does not exhibit the standard form expected for FTs and

Green-Kubo and Einstein expressions for the transport coefficients of a fluid in a nonequilibrium steady state can be derived using the Fluctuation Theorem and by assuming the probability distribution of the time-averaged dissipative flux is Gaussian. These expressions are consistent with those obtained using linear response theory and are valid in the linear regime. It is shown that these expressions are however, not valid in the nonlinear regime where the fluid is driven far from equilibrium. We advance an argument for why these expressions are only valid in the linear response, zero field limit.

For thermostatted dissipative systems the Fluctuation Theorem gives an analytical expression for the ratio of probabilities that the time averaged entropy production in a finite system observed for a finite time, takes on a specified value compared to the negative of that value. Hitherto it had been thought that the presence of some thermostatting mechanism was an essential component of any system which satisfies a Fluctuation Theorem. In the present paper we show that a Fluctuation Theorem can be derived for purely Hamiltonian systems, with or without applied dissipative fields.

The fluctuation relation of the Gallavotti-Cohen Fluctuation Theorem (GCFT) concerns fluctuations in the phase space compression rate of dissipative, reversible dynamical systems. It has been proven for Anosov systems, but it is expected to apply more generally. This raises the question of which non-Anosov systems satisfy the fluctuation relation. We analyze time dependent fluctuations in the phase space compression rate of a class of N-particle systems that are at equilibrium or in near equilibrium steady states. This class does not include Anosov systems or isoenergetic systems, however, it includes most steady state systems considered in molecular dynamics simulations of realistic systems. We argue that the fluctuations of the phase space compression rate of these systems at or near equilibrium do not satisfy the fluctuation relation of the GCFT, although the discrepancies become somewhat smaller as the systems move further from equilibrium. In contrast, similar fluctuation relations for an appropriately defined dissipation function appear to hold both near and far from equilibrium.

The fluctuation theorem ͑FT͒ is a generalization of the second law of thermodynamics that applies to small systems observed for short times. For thermostated systems it gives the probability ratio that entropy will be consumed rather than produced. In the present paper, we propose a version of the FT that applies to thermostated dissipative systems which respond to time-dependent dissipative fields. In testing the time-dependent fluctuation theorem we provide convincing evidence that sets of trajectories with conjugate values for the time-integrated entropy production, (ϮAϮ␦A), are indeed ͑for time-reversible dynamical systems such as those studied here͒, time-reversal images of one another. This observation verifies the deep connection between time-reversal symmetry, the fluctuation theorem, and the second law of thermodynamics.

Active matter and driven systems exhibit statistical fluctuations in density and particle positions, providing an indirect indicator of dissipation across multiple length and time scales. Here, we quantitatively relate these measurable fluctuations to a thermodynamic speed limit that constrains the rates of heat and entropy production in nonequilibrium processes. By reparametrizing the speed limit, we show how to infer heat and entropy production rates from directly observable or controllable quantities. This approach can use available experimental data and avoid the need for analytically solvable microscopic models or full time-dependent probability distributions. The heat rate we predict agrees with experimental measurements for a Brownian particle and a microtubule active gel, which validates the approach and suggests potential for the design of experiments.

We study the heat transfer between two finite quantum systems initially at different temperatures. We find that a recently proposed fluctuation theorem for heat exchange, namely the exchange fluctuation theorem [C. Jarzynski and D. K. Wójcik, Phys. Rev. Lett. 92 (2004), 230602], does not generally hold in the presence of a finite heat transfer as in the original form proved for weak coupling. As the coupling is weakened, the deviation from the theorem and the heat transfer vanish in the same order of the coupling. We then discover a condition for the exchange fluctuation theorem to hold in the presence of a finite heat transfer, namely the commutable-coupling condition. We explicitly calculate the deviation from the exchange fluctuation theorem as well as the heat transfer for simple models. We confirm for the models that the deviation indeed has a finite value as far as the coupling between the two systems is finite except for the special point of the commutable-coupling condition. We also confirm analytically that the commutable-coupling condition indeed lets the exchange fluctuation theorem hold exactly under a finite heat transfer.