Nonequilibrium statistical mechanics

In their recent paper and the associated Response to this Comment, Tuckerman et al. dispute the form of the Liouville equation, as proposed by Liouville in 1838. They go on to introduce a definition of the entropy which is at variance with Boltzmann’s H-function and with Gibbs’ definition of entropy. They argue that their “entropy” is a constant of the motion, equal to its initial equilibrium value regardless of the imposition of external fields. We argue that the analysis of Tuckerman et al. is incorrect and that issues raised by Tuckerman et al. are not at all new but have already been correctly incorporated into nonequilibrium statistical mechanics.  

The photon diffusion equation is solved making use of the Born series for the Robin boundary condition. We develop a general theory for arbitrary domains with smooth enough boundaries and explore the convergence. The proposed Born series is validated by numerical calculation in the threedimensional half space. It is shown that in this case the Born series converges regardless the value of the impedance term in the Robin boundary condition.

Nonequilibrium thermodynamics describes the rates of transport phenomena with the aid of various thermodynamic forces, but often the phenomenological transport coefficients are not known, and the description is not easily connected with equilibrium relations. We present a simple and intuitive model to address these issues. Our model is based on Lagrangian dynamics for chemical systems with dissipation, so one may think of the model as physicochemical mechanics. Using one main equation, the model allows a systematic derivation of all transport and equilibrium equations, subject to the limitation that heat generated or absorbed in the system must be small for the model to be valid. A table with all major examples of transport and equilibrium processes described using physicochemical mechanics is given. In equilibrium, physicochemical mechanics reduces to standard thermodynamics and the Gibbs-Duhem relation, and we show that the First and Second Laws of thermodynamics are satisfied for...

We consider an Ising model where longitudinal components of every pair of spins have antiferromagnetic interaction of the same magnitude. When subjected to a transverse magnetic field at zero temperature, the system undergoes a phase transition of second order to an ordered phase and if the temperature is now increased, there is another phase transition to disordered phase. We provide derivation of these features by perturbative treatment up to the second order and argue that the results are non-trivial and not derivable from the known results about related models.

Cantor Dust (CD) is a hypothetical Dark Matter (DM) condensate of relic spacetime dimensions left over from the primordial Universe. A plausible assumption is that, in the complex dynamic regime of primordial cosmology, CD consists of continuous dimensional fluctuations acting as a fractal mass distribution. Starting from these premises, here we study the gravitational behavior of CD in the context of Rényi and Tsallis entropies. Our findings offer a fresh perspective on structure formation as a complex dynamical process.

The Accardi-Boukas quantum Black-Scholes equation ([1]) can be used as an alternative to the classical approach to finance, and has been found to have a number of useful benefits. The quantum Kolmogorov backward equations, and associated quantum Fokker-Planck equations, that arise from this general framework, are derived using the Hudson-Parthasarathy quantum stochastic calculus ([14]). In this paper we show how these equations can be derived using a nonlocal approach to quantum mechanics. We show how nonlocal diffusions, and quantum stochastic processes can be linked, and discuss how moment matching can be used for deriving solutions.

We consider the multiplicity and stability of subharmonic solutions of discrete dynamic systems with periodic perturbations, whose existence was established in the first part of this series. Under the hypotheses that the perturbation is locally Lipschitz continuous, we determine the precise number of subharmonic solutions, and we also show that these subharmonic solutions are stable (unstable) provide the periodic orbit of the unperturbed system is stable (unstable).

We study the low temperature behaviour of path integrals for a simple one-dimensional model. Starting from the Feynman-Kac formula, we derive a new functional representation of the density matrix at finite temperature, in terms of the occupation times of Brownian motions constrained to stay within boxes with finite sizes. From that representation, we infer a kind of ergodic approximation, which only involves double ordinary integrals. As shown by its applications to different confining potentials, the ergodic approximation turns out to be quite efficient, especially in the low-temperature regime where other usual approximations fail.

This article reviews recent theoretical developments in heavy-quarkonium physics from the point of view of effective-field theories of QCD. We discuss nonrelativistic QCD and concentrate on potential nonrelativistic QCD. The main goal will be to derive Schrödinger equations based on QCD that govern heavy-quarkonium physics in the weak-and strong-coupling regimes. Finally, the review discusses a selected set of applications, which include spectroscopy, inclusive decays, and electromagnetic threshold production.

We proposed a toy model of granular compaction which includes some resistance due to granular arches. In this model, the solid/solid friction of contacting grains is a key parameter and a slipping threshold wc is defined. Realistic compaction behaviors have been obtained. Two regimes separated by a critical point w * c of the slipping threshold have been emphasized : (i) a slow compaction with lots of paralyzed regions, and (ii) an inverse logarithmic dynamics with a power law scaling of grain mobility. Below the critical point w * c , the physical properties of this frozen system become independent of wc. Above the critical point w * c , i.e. for low friction values, the packing properties behave as described by the classical Janssen theory for silos.

We present an original experimental study of the slow compaction dynamics for twodimensional isotropic granular systems. Compaction dynamics is measured at three different scales : the macroscopic scale through the normalized packing fraction ρ, the mesoscopic scale through the normalized fraction φ of domains ideally ordered in the system, and the microscopic scale through the grain mobility μ. The domains ideally ordered are found to obey a growth process dominated by the displacement of domain boundaries. We present also preliminary results of three-dimensional simulations with a model of contact dynamics. These results allow to discuss the difference between the two-dimensional and the three-dimensional cases.

Recently we have demostrated that the nonextensitivity parameter q occuring in some applications of Tsallis statistics (known also as index of the corresponding Lévy distribution) is, in q > 1 case, given entirely by the fluctuations of the parameters of the usual exponential distribution. We show here that this interpretation is valid also for the q < 1 case. The parameter q is therefore a measure of fluctuations of the parameters of the usual exponential distribution.

The equation of motion for a driven fractional oscillator is formulated by replacing the classical second-order time derivative with a Caputo fractional derivative of order 1 < 𝛼 ≤ 2. In this study, the Sumudu transform method is employed to obtain an analytical solution of the fractional differential equation. By utilizing the integral properties of the Sumudu transform, which are adapted for Caputo fractional derivatives, the system's response is explicitly derived in the time domain. The dynamic characteristics and phase plane trajectories of the fractional oscillator are analyzed for various values of 𝛼. The results demonstrate that the Sumudu transform provides an effective and accurate framework for analyzing the complex behavior of fractional oscillatory systems.

Muitifractal analysis of generalized luminosity fields gives evidence that the spatio-luminous distribution of galaxies in the observable universe has characteristic features of a phase transition from random fractality to homogeneity on large scales.

The booklet represents a viewpoint, my personal, and does not pretend to be exhaustive: many important topics have been left out (like [8, 62, 120, 40], just to mention a few works that have led to further exciting developments). I have tried to present a consistent theory including some of its unsatisfactory aspects. The Collected papers of Boltzmann, Clausius, Maxwell are freely available: about Boltzmann I am grateful (and all of us are) to Wolfgang Reiter, in Vienna, for actively working to obtain that Österreichische Zentralbibliothek für Physik undertook and accomplished the task of digitizing the "Wissenschaftliche Abhandlungen" and the "Populäre Schriften" at object/o:63668 object/o:63638 respectively, making them freely available. Acknowledgments: I am indebted to D. Ruelle for his teaching and examples. I am indebted to E.G.D. Cohen for his constant encouragement and stimulation as well as, of course, for his collaboration in the developments in our common works and for supplying many ideas and problems. To Guido Gentile and Alessandro Giuliani for their close collaboration in an attempt to study heat conduction in a gas of hard spheres. Finally a special thank is to Professor Wolf Beiglöck for his constant interest and encouragement.

The equation of motion for a driven fractional oscillator is formulated by replacing the classical second-order time derivative with a Caputo fractional derivative of order 1 < 𝛼 ≤ 2. In this study, the Sumudu transform method is employed to obtain an analytical solution of the fractional differential equation. By utilizing the integral properties of the Sumudu transform, which are adapted for Caputo fractional derivatives, the system's response is explicitly derived in the time domain. The dynamic characteristics and phase plane trajectories of the fractional oscillator are analyzed for various values of 𝛼. The results demonstrate that the Sumudu transform provides an effective and accurate framework for analyzing the complex behavior of fractional oscillatory systems.

The object of this brief note is to point out that a spacetime endowed with continuous dimensions can be interpreted as dual to classical gravitation in four dimensions. This observation sheds unexpected light onto the gravitational behavior of Cantor Dust (CD), a hypothetical large-scale topological condensate of relic dimensions left over from the primordial stages of Universe evolution.

The Aurora Model of Intelligence describes intelligence as an emergent phenomenon in open, dynamic systems managing entropy through structured adaptation. Integrating principles from thermodynamics, complex systems theory, neuroscience, and network science, Aurora outlines how intelligence evolves via non-linear dynamics, critical transitions, fractal structures, and inter-system interactions. It proposes a dynamic ethical framework focused on preserving and enhancing coherence in an entropic universe, offering a scalable blueprint for building resilient, evolutionary, and ethically aligned artificial intelligences.

Relaxation process is the spontaneous transition of an isolated system from one to another macroscopic state. It is assumed that the entropy increase associated with this process is a functional of dynamical variables (fluxes). This fact makes entropy production a dynamical variable. It is shown within Jaynes' MaxEnt formalism that almost all possible microscopic fluxes are accompanied by maximal entropy production. Using Einstein's formula for probability of fluctuation, we obtain that the probability of the change in entropy is proportional to the exponential function of the entropy change divided by the Boltzmann constant. This result is applied to the system close to the equilibrium and the well-known relationships between thermodynamic forces and fluxes are reproduced.

A distinguishing feature of active particles is the nature of the non-equilibrium noise driving their dynamics. Control of these noise properties is, therefore, of both fundamental and applied interest. We demonstrate emergent tuning of the active noise of a granular self-propelled particle by confining it to a quasi one-dimensional channel. We find that this particle, moving like an active Brownian particle (ABP) in two-dimensions, displays run-and-tumble (RTP) characteristics in confinement. We show that the dynamics of the relative orientation co-ordinate of the particle maps to that of a Brownian particle in a periodic potential subject to a constant force, in analogy to the dynamics of a molecular motor. This mapping captures the essential statistical characteristics of the one-dimensional RTP motion. Specifically, our theoretical analysis is in agreement with the empirical distributions of the relative orientation co-ordinate and the run-times (tumble-rates) of the particle. F...

We consider an ideal Fermi gas confined to a geometric structure consisting of a central region – the sample – connected to several infinitely extended ends—the reservoirs. Under physically reasonable assumptions on the propagation properties of the one-particle dynamics within these reservoirs, we show that the state of the Fermi gas relaxes to a steady state. We compute the expected value of various current observables in this steady state and express the result in terms of scattering data, thus obtaining a geometric version of the celebrated Landauer-Büttiker formula.

The quantum fluctuations of the entropy production for fermionic systems in the Landauer-Büttiker nonequilibrium steady state are investigated. The probability distribution, governing these fluctuations, is explicitly derived by means of quantum field theory methods and analyzed in the zero frequency limit. It turns out that microscopic processes with positive, vanishing and negative entropy production occur in the system with nonvanishing probability. In spite of this fact, we show that all odd moments (in particular, the mean value of the entropy production) of the above distribution are non-negative. This result extends the second principle of thermodynamics to the quantum fluctuations of the entropy production in the Landauer-Büttiker state. The effect of the time reversal is also discussed.

We investigate the coarsening dynamics of a simplified version of the persistent voter model in which an agent can become a zealot-i.e. resistent to change opinion-at each step, based on interactions with its nearest neighbors. We show that such a model captures the main features of the original, non-Markovian, persistent voter model. We derive the governing equations for the one-point and two-point correlation functions. As these equations do not form a closed set, we employ approximate closure schemes, whose validity was confirmed through numerical simulations. Analytical solutions to these equations are obtained and well agree with the numerical results.

We solve a non-equilibrium statistical mechanics problem exactly, namely, the single-file dynamics of N hard-core interacting particles (the particles cannot pass each other) of size ∆ diffusing in a one dimensional system of finite length L with reflecting boundaries at the ends. We obtain an exact expression for the conditional probability density function ρT (yT , t|yT ,0) that a tagged particle T (T = 1, ..., N ) is at position yT at time t given that it at time t = 0 was at position yT ,0. Using a Bethe ansatz we obtain the N -particle probability density function, and by integrating out the coordinates (and averaging over initial positions) of all particles but particle T , we arrive at an exact expression for ρT (yT , t|yT ,0) in terms of Jacobi polynomials or hypergeometric functions. Going beyond previous studies, we consider the asymptotic limit of large N , maintaining L finite, using a non-standard asymptotic technique. We derive an exact expression for ρT (yT , t|yT ,0) for a tagged particle located roughly in the middle of the system, from which we find that there are three time regimes of interest for finite-sized systems: (A) For times much smaller than the collision time t ≪ τ coll = 1/(̺ 2 D), where ̺ = N/L is the particle concentration and D the diffusion constant for each particle, the tagged particle undergoes normal diffusion; (B) for times much larger than the collision time t ≫ τ coll but times smaller than the equilibrium time t ≪ τeq = L 2 /D we find a single-file regime where ρT (yT , t|yT ,0) is a Gaussian with a mean square displacement scaling as t 1/2 ; (C) For times longer than the equilibrium time t ≫ τeq, ρT (yT , t|yT ,0) approaches a polynomialtype equilibrium probability density function. Notably, only regimes (A) and (B) are found in the previously considered infinite systems.

We present a model of speech perception which takes into account effects o correlations between sounds. Words in this model correspond to the attractors of a suitably chosen descent dynamics. The resulting lexicon is rich in short words, and much less so in longer ones, as befits a reasonable word length distribution. We separately examine the decryption of short and long words in the presence of mishearings. In the regime of short words, the algorithm either quickly retrieves a word, or proposes another valid word. In the regime of longer words, the behaviour is markedly different. While the successful decryption of words continues to be relatively fast, there is a finite probability of getting lost permanently, as the algorithm wanders round the landscape of suitable words without ever settling on one.

It was recently conjectured that the Standard Model of particle physics resides on a bifurcation diagram generated by the recursive scaling of Higgs coupling. This sequel explores the relationship between the bifurcation diagram and the Path Integral (PI) formalism of Quantum Field Theory (QFT). The long-term goal is to base the Feynman diagrams on the properties of the Feigenbaum attractor of either quadratic or cubic maps.

As paradigm of complex behavior, multifractals describe the underlying geometry of self-similar objects or processes. Building on the connection between Rényi entropy and multifractals, we speculate here that the generalized dimension of geodesic trajectories in General Relativity reproduces the four-dimensionality of classical spacetime.

The 2017 Snook Prize has been awarded to Kenichiro Aoki for his exploration of chaos in Hamiltonian φ 4 models. His work addresses symmetries, thermalization, and Lyapunov instabilities in few-particle dynamical systems. A companion paper by Timo Hofmann and Jochen Merker is devoted to the exploration of generalized Hénon-Heiles models and has been selected for Honorable Mention in the Snook-Prize competition.

Over the decades, Functional Analysis has been enriched and inspired on account of demands from neighboring fields, within mathematics, harmonic analysis (wavelets and signal processing), numerical analysis (finite element methods, discretization), PDEs (diffusion equations, scattering theory), representation theory; iterated function systems (fractals, Julia sets, chaotic dynamical systems), ergodic theory, operator algebras, and many more. And neighboring areas, probability/statistics (for example stochastic processes, Ito and Malliavin calculus), physics (representation of Lie groups, quantum field theory), and spectral theory for Schrodinger operators. We have strived for a more accessible book, and yet aimed squarely at applications; -- we have been serious about motivation: Rather than beginning with the four big theorems in Functional Analysis, our point of departure is an initial choice of topics from applications. And we have aimed for flexibility of use; acknowledging that...

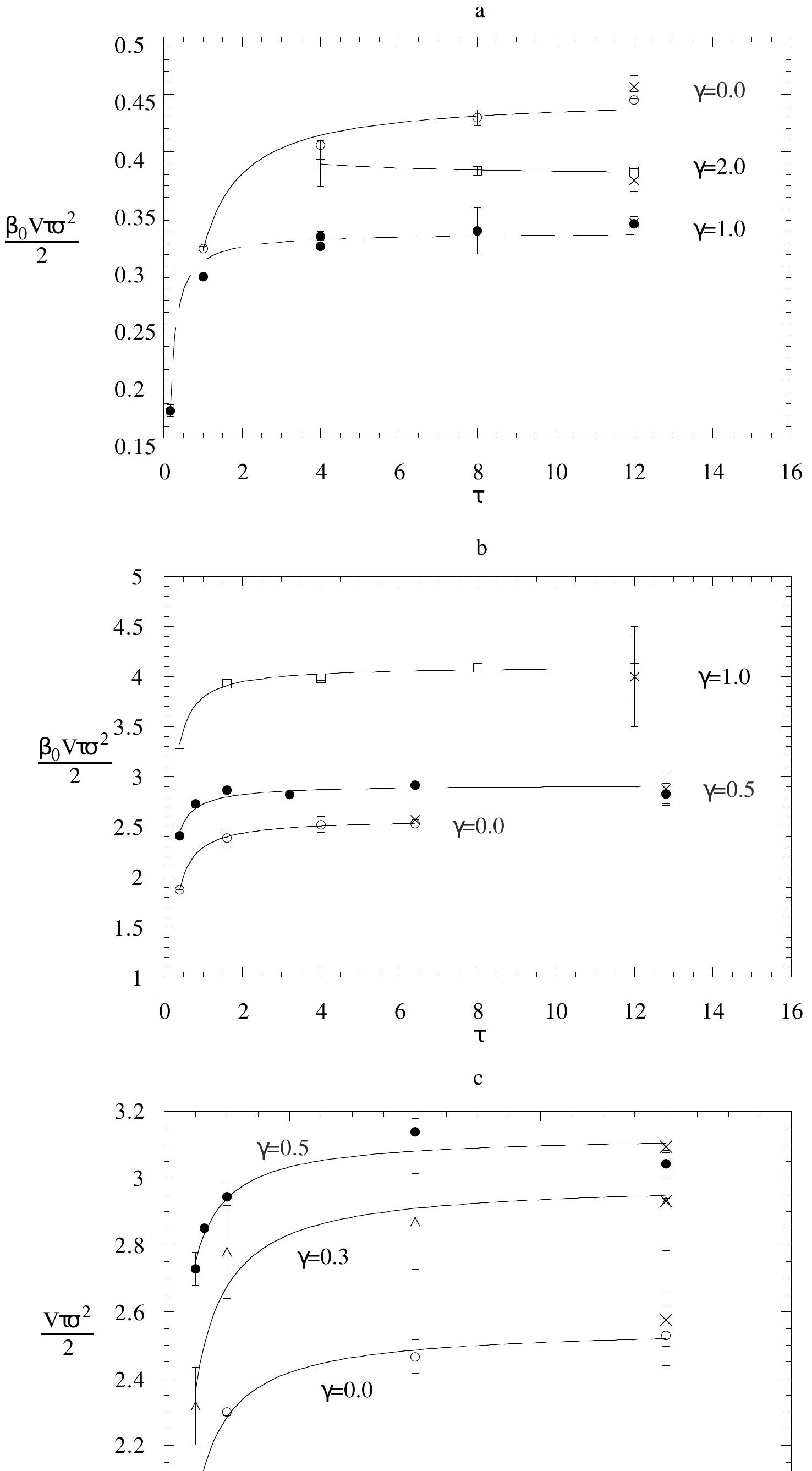
͑TMBK͒ ͑Ref. 1͒ state that using a conserved ''energy'' HЈ, enables them to derive a nonequilibrium steady state distribution function directly from the equilibrium microcanonical distribution function. There is, however, no justification for their application of Boltzmann's equilibrium equal-a-prioriprobability assumption, away from equilibrium. The equala-priori assumption applies only to isolated equilibrium systems, and is conventionally used to justify equilibrium distribution functions. In 1838 Liouville derived an equation of motion for the normalised nonequilibrium probability density, f (⌫,t), of observing a phase ⌫ϵ(x 1 ,y 1 ,z 1 ,x 2 ,...,p xN ,p yN ,p zN ), for an N-particle system in a three-dimensional Cartesian space, at time t. In modern notation the equation he derived reads, 2

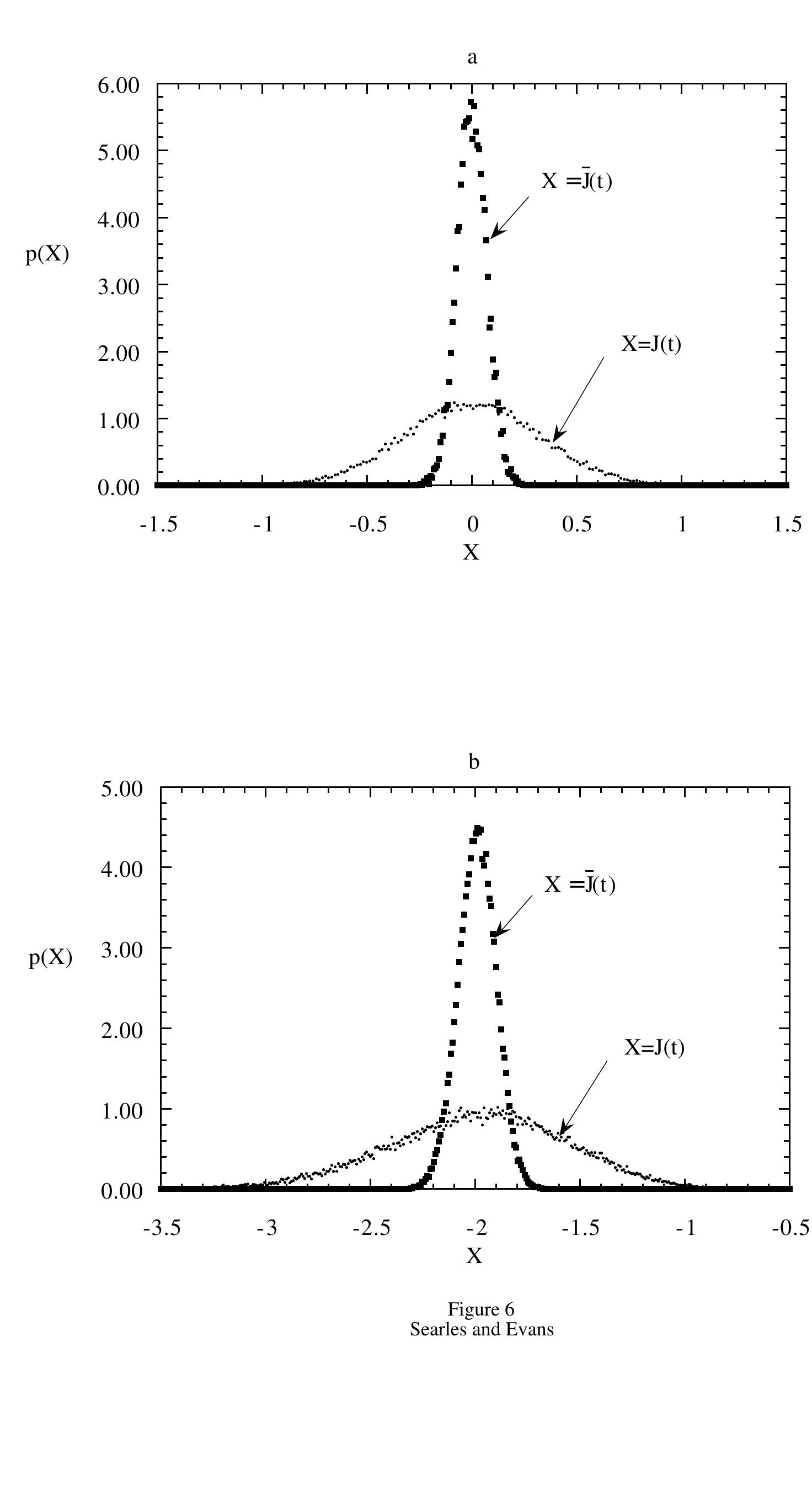
The Fluctuation Theorem (FT) gives an analytic expression for the probability, in a nonequilibrium system of finite size observed for a finite time, that the dissipative flux will flow in the reverse direction to that required by the Second Law of Thermodynamics. In the present letter a Local version of the Fluctuation Theorem (LFT), is derived. We find that in the case of planar Poiseuille flow of a Newtonian fluid between thermostatted walls, nonequilibrium molecular dynamics simulation results support LFT.

Green-Kubo and Einstein expressions for the transport coefficients of a fluid in a nonequilibrium steady state can be derived using the Fluctuation Theorem and by assuming the probability distribution of the time-averaged dissipative flux is Gaussian. These expressions are consistent with those obtained using linear response theory and are valid in the linear regime. It is shown that these expressions are however, not valid in the nonlinear regime where the fluid is driven far from equilibrium. We advance an argument for why these expressions are only valid in the linear response, zero field limit.

The outstanding properties of cerium oxide from its capacity to transit from Ce 3+ to Ce 4+ (and from Ce 4+ to Ce 3+) make it very useful for a wide range of technological applications of great importance. We performed experiments sending pulses of CO that interact with the surface of nano cubes of CeO 2 with low index faces (100). We model this process through the statistical description of the creation of oxygen vacancies leading to the appearance of Ce 2 O 3. The model is able to predict the composition of the equilibrium nano cubes surface under different experimental conditions. The theoretical results are compared with the obtained experimental values of CO consumption, which is related to the presence of Ce 3+ atoms.

We study thermal transport induced by soliton dynamics in a long Josephson tunnel junction operating in the flux-flow regime. A thermal bias across the junction is established by imposing the superconducting electrodes to reside at different temperatures, when solitons flow along the junction. Here, we consider the effect of both a bias current and an external magnetic field on the thermal evolution of the device. In the flux-flow regime, a chain of magnetically-excited solitons rapidly moves along the junction driven by the bias current. We explore the range of bias current triggering the flux-flow regime at fixed values of magnetic field, and the stationary temperature distribution in this operation mode. We evidence a steady multi-peaked temperature profile which reflects on the average soliton distribution along the junction. Finally, we analyse also how the friction affecting the soliton dynamics influences the thermal evolution of the system.

We start with reviewing the origin of the idea that entropy and the Second Law are associated with the Arrow of Time. We then introduced a new definition of entropy based on Shannon’s Measure of Information (SMI). The SMI may be defined on any probability distribution; and therefore it is a very general concept. On the other hand entropy is defined on a very special set of probability distributions. More specifically the entropy of a thermodynamic system is related the probability distribution of locations and velocities (or momenta) of all the particles, which maximized the Shannon Measure of Information. As such, entropy is not a function of time. We also show that the H-function, as defined by Boltzmann is an SMI but not entropy. Therefore, while the H-function, as an SMI may change with time, Entropy, as a limit of the SMI does not change with time.

We present calculations of the coarse-grained entropy Scg(t) for the model of a classical point particle enclosed in a two-dimensional box with perfectly reflecting walls. We find in comparison with the one-dimensional case that the fluctuations of Scg(t) and of the expectation values of the position have decreased, and that Scg(t) does not take its asymptotic value at regular time intervals. The times after which Scg(t) and the expectation values have approximately reached their equilibrium values, are about equal; recurrence times are rather clearly separated from this time. Finally, we give a general estimate on the change of an expectation value due to a refinement of the cells.

Numerical simulations of systems at coexistence are known to yield unstable fields in some regions of the density parameters, as well as inequivalence of ensembles. The ‘Van der Waals-like’ loops are attributed to effects of the interface between the coexisting phases, but the question of convexity remains unresolved. We recover the theory developed by Hill in the 1960’s, and adapt it to include the interface free energy. Our adapted theory is verified through carefully planned simulations, and give a thermodynamic description of the interface behaviour inside the coexistence region which restores the proper convexity of the thermodynamic potentials, as well as yields convergence of grandcanonical and canonical results. As a bonus, our interpretation allows direct calculation of surface tension in very good accordance with Onsager’s analytic prediction.

Run-and-tumble particles confined between two walls seem like a simple enough problem to possess analytical tractability. Yet, to date no satisfactory analysis is available for dimensions higher than one. This work contributes to the theoretical understanding of this system by reinterpreting it as a splitting probability problem. Such reinterpretation permits us to formulate the problem as the integral equation, rather than a more standard formulation based on the Fokker–Planck equation. In addition to providing an analogy with another phenomenon, the reinterpretation permits a new type of analysis, yields useful results, and offers some analytical tractability.

Systems Biology (system-level understanding in biological science), from the physical-chemical point of view, is involved with irreversible thermodynamics and nonlinear kinetic theory of open systems which are founded on nonequilibrium statistical mechanics. We describe a modern thermo-statistical approach for dealing with complex systems, in particular biological systems. We consider the case of a very peculiar complex behavior in open boson systems sufficiently away, from equilibrium, which appear to have large relevance in the functioning of biological systems. This is, on the one hand, the so-called Fröhlich-Bose-Einstein-like condensation leading in steady-state conditions to the emergence of a particular case of quantum-large-scale coherent ordering, of the type of a selforganizing-synergetic dissipative structure. Moreover, additional complexity emerges in the form of propagation, in this condensate, of signals (information) consisting of nearly undamped and undistorted, long-distance propagating, solitary waves (the pseudoparticle soliton). It can be accompanied by a so-called Fröhlich-Cherenkov cone of emission of polar vibrations, and it is also possible the formation of metastable states of the form of the so-called bioelectrets. These are phenomena apparently working in biological processes, which are presently gaining relevant status on the basis of eventually providing a large-scale quantum-coherent behavior in cytoskeletons of neurons and the conscious (non-computational) activity in the brain. Emphasis is centered on the quantum-mechanical-statistical irreversible thermodynamics of these open systems, and the informational characteristics of the phenomena. Ways for their experimental evidencing are pointed out and discussed.

Critical phenomena describe continuous phase transitions characterized by power-law divergences, universality of scaling exponents and ergodicity breaking. Scaling exponents depend on the dimension of the underlying spacetime (d) and, in many cases, also on the dimension of variables defining criticality (D). Recent studies suggest that both dimensions (d and D) run the observation scale and, as a result, determine the rate of divergence near critical points. Building on these observations, the goal of this report is to close the gap between critical behavior in continuous dimensions and the anomalous findings of the James Webb Space Telescope (JWST).

Using the Fluctuation Theorem (FT), we give a first-principles derivation of Boltzmann's postulate of equal a priori probability in phase space for the microcanonical ensemble. Using a corollary of the Fluctuation Theorem, namely the Second Law Inequality, we show that if the initial distribution differs from the uniform distribution over the energy hypersurface, then under very wide and commonly satisfied conditions, the initial distribution will relax to that uniform distribution. This result is somewhat analogous to the Boltzmann H-theorem but unlike that theorem, applies to dense fluids as well as dilute gases and also permits a nonmonotonic relaxation to equilibrium. We also prove that in ergodic systems the uniform (microcanonical) distribution is the only stationary, dissipationless distribution for the constant energy ensemble.

We study the ordering kinetics of a generalization of the voter model with long-range interactions, the p-voter model, in one dimension. It is defined in terms of boolean variables Si, agents or spins, located on sites i of a lattice, each of which takes in an elementary move the state of the majority of p other agents at distances r chosen with probability P (r) ∝ r −α. For p = 2 the model can be exactly mapped onto the case with p = 1, which amounts to the voter model with long-range interactions decaying algebraically. For 3 ≤ p < ∞, instead, the dynamics falls into the universality class of the one-dimensional Ising model with long-ranged coupling constant J(r) = P (r) quenched to small finite temperatures. In the limit p → ∞, a crossover to the (different) behavior of the long-range Ising model quenched to zero temperature is observed. Since for p > 3 a closed set of differential equations cannot be found, we employed numerical simulations to address this case.

The notion of local energy and momentum conservation in a nuclear reaction provide a foundation of nuclear physics. Classical models for energy and momentum conservation were used as a way to understand nuclear scattering experiments in the time of Rutherford [1]. Energy

We continue our study of the linear response of a nonequilibrium system. This Part II concentrates on models of open and driven inertial dynamics but the structure and the interpretation of the result remain unchanged: the response can be expressed as a sum of two temporal correlations in the unperturbed system, one entropic, the other frenetic. The decomposition arises from the (anti)symmetry under time-reversal on the level of the nonequilibrium action. The response formula involves a statistical averaging over explicitly known observables but, in contrast with the equilibrium situation, they depend on the model dynamics in terms of an excess in dynamical activity. As an example, the Einstein relation between mobility and diffusion constant is modified by a correlation term between the position and the momentum of the particle.

As of today, Quantum Field Theory (QFT) and General Relativity (GR) are broadly recognized paradigms of foundational physics. There are, however, growing suspicions that both paradigms fail to hold somewhere above the Standard Model (SM) scale and in the realm of primordial cosmology. Evidence collected on multiple fronts indicates that emergence and complexity are universal features of far-from-equilibrium systems with many degrees of freedom. In line with these findings, Part 1 of this report explores the complex dynamics of evolving dimensional fluctuations beyond the SM scale. Part 2 outlines the role of complex dynamics in the nonintegrable sector of particle physics, Dark Matter condensation and the gravitational regime of the early Universe.