Denis Evans
580 California St., Suite 400
San Francisco, CA, 94104
The fluctuation theorem and Green–Kubo relations
2000, Journal of Chemical Physics
Sign up for access to the world's latest research
Abstract
Green-Kubo and Einstein expressions for the transport coefficients of a fluid in a nonequilibrium steady state can be derived using the Fluctuation Theorem and by assuming the probability distribution of the time-averaged dissipative flux is Gaussian. These expressions are consistent with those obtained using linear response theory and are valid in the linear regime. It is shown that these expressions are however, not valid in the nonlinear regime where the fluid is driven far from equilibrium. We advance an argument for why these expressions are only valid in the linear response, zero field limit.
Key takeaways
AI
AI
- The Fluctuation Theorem (FT) connects dissipative flux probabilities in nonequilibrium steady states to Gaussian distributions.
- Green-Kubo relations derived from FT hold only in the linear response regime, failing in nonlinear cases.
- NEMD simulations indicate that the nonlinear Green-Kubo relations are invalid when driven far from equilibrium.
- Transport coefficients can be calculated using the variance of time-averaged fluxes in the zero field limit.
- Research shows that deviations from Gaussian behavior contribute to the breakdown of nonlinear Green-Kubo expressions.
Figures (8)
References (27)
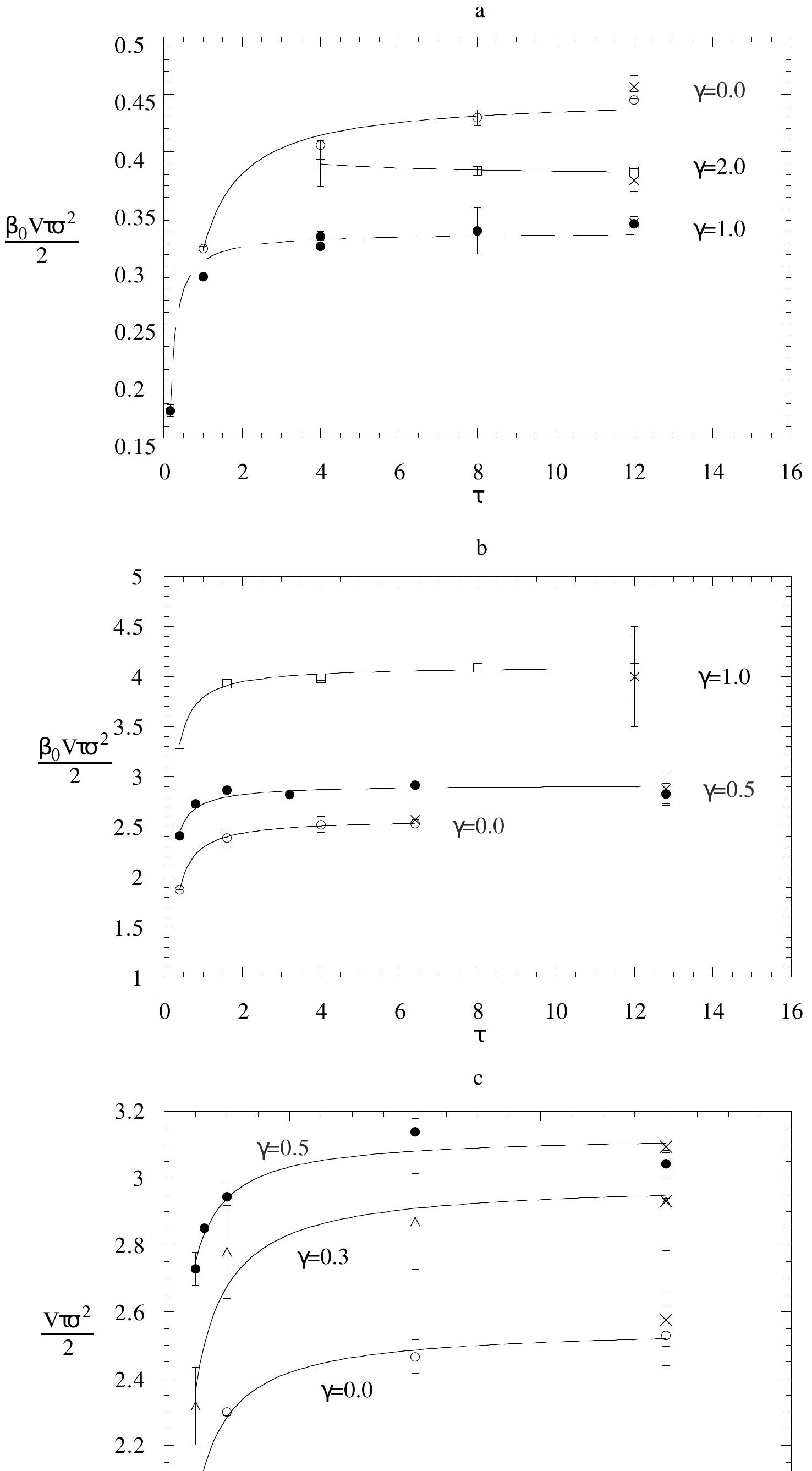
- This is in agreement with experimental observations given in Figures 4(a),(b), 4(c). References
- D. J. Evans, E. G. D. Cohen and G. P. Morriss, Phys. Rev. Lett., 71, 2401 (1993).
- J-P. Eckmann and I. Procaccia, Phys. Rev. A, 34, 659 (1986).
- D. J. Evans and D. J. Searles, Phys. Rev. E, 50, 1645 (1994).
- D. J. Evans and D. J. Searles, Phys. Rev. E, 52, 5839 (1995).
- D. J. Evans and D. J. Searles, Phys. Rev. E, 53, 5808 (1996).
- G. Gallavotti and E. G. D. Cohen, J. Stat. Phys., 80, 931 (1995).
- G. Gallavotti and E. G. D. Cohen, Phys. Rev. Letts., 74, 2694 (1995).
- G. Ayton and D. J. Evans, J. Stat. Phys., 97, 811 (1999);
- E. G. D. Cohen and G. Gallavotti, J. Stat. Phys., 96, 1343 (1999).
- D. J. Searles and D. J. Evans, Phys. Rev. E, 60, 159 (1999).
- J. L. Lebowitz and H. Spohn, J. Stat. Phys., 95, 333 (1999).
- J. Kurchan, J. Phys. A, 31, 3719 (1998).
- C. Maes, J. Stat. Phys., 95, 367 (1999).
- H. Cramér, Mathematical methods of statistics, (Princeton University Press, Princeton, 1966).
- H. Cramér, Random variables and probability distributions, (Cambridge University Press, London, 1970);
- B. V. Gnedenko and A. N. Kolmogorov, Limit distributions for sums of independent random variables, (Addison-Wesley, Massachusetts, 1954).
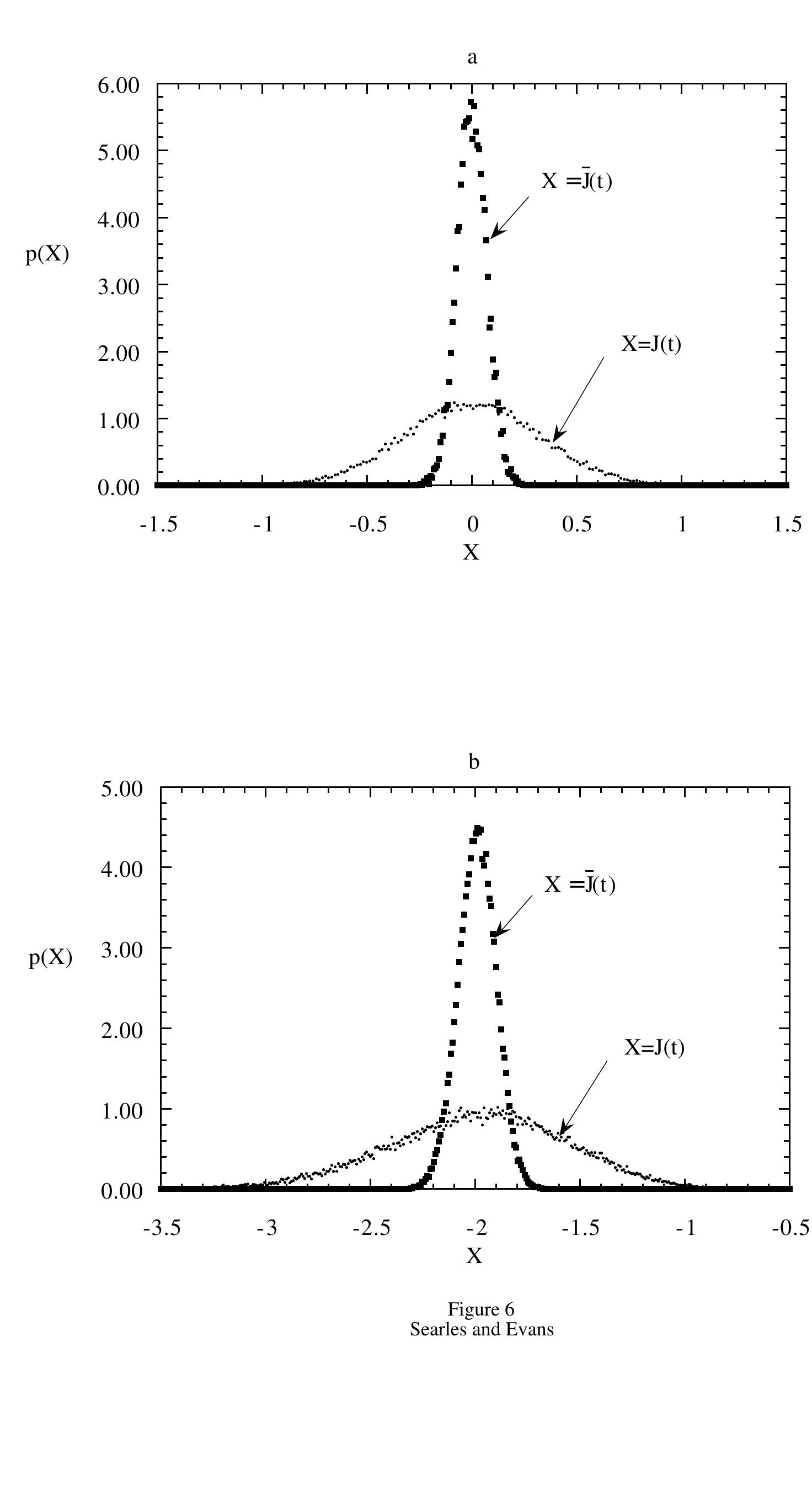
- CLT states that under quite general conditions [13, 14], the mean of an infinite set of independent variables is normally distributed, independent of the distribution of the individual independent variables. However, for a finite number of variables, unless the
- D. J. Evans and G. P. Morriss, Statistical Mechanics of Nonequilibrium Liquids (Academic Press, London, 1990).
- D. J. Searles and D. J. Evans, "Ensemble dependence of the transient fluctuation theorem", http://xxx.lanl.gov/abs/cond-mat/9906002.
- Note that a Gaussian distribution does not imply a FT. The FT is a much stronger statement: it specifies the relationship between the mean and the standard deviation if the distribution is Gaussian. We note that the FT of course, does not require the distribution to be Gaussian.
- D. J. Evans and G. P. Morriss, Phys. Rev. A, 31, 3817 (1985).
- G. Gallavotti, Phys. Rev. Letts, 77, 4334 (1996).
- F. Bonetto, G. Gallavotti and P. L. Garrido, Physica D, 105, 226 (1997).
- F. Bonetto, N. I. Chernov and J. L. Lebowitz, Chaos, 8, 823 (1998).
- We assume that the FT and equations (23) and (30) have reached their limiting behaviour at that time.
- A similar argument can be used if we take the thermodynamic limit, in which the distribution collapses onto a delta function at the mean. In this case a GK expression is valid for large systems provided the distribution of the time-averaged fluxes is Gaussian at a minimal volume.