Fixed Point Theory Research Papers

Mean Shift, Mode Seeking, and Clustering

1995, IEEE Transactions on Pattern Analysis and Machine Intelligence

Mean shift, a simple iterative procedure that shifts each data point to the average of data points in its neighborhood, is generalized and analyzed in this paper. This generalization makes some k-means like clustering algorithms its... more

descriptionView Paper arrow_downwardDownload

A framework for uplink power control in cellular radio systems

by Roy Yates

1995, IEEE Journal on Selected Areas in Communications

In cellular wireless communication systems, transmitted power is regulated to provide each user an acceptable connection by limiting the interference caused by other users. Several models have been considered including: (1) xed base... more

descriptionView Paper arrow_downwardDownload

A general purpose model for the condensed phases of water: TIP4P/2005

by Carlos Vega

2005, Chemical Physics

A potential model intended to be a general purpose model for the condensed phases of water is presented. TIP4P/2005 is a rigid four site model which consists of three fixed point charges and one Lennard-Jones center. The parametrization... more

descriptionView Paper arrow_downwardDownload

Constructing Free-Energy Approximations and Generalized Belief Propagation Algorithms

by Yair Weiss

2005, IEEE Transactions on Information Theory

Note: This technical report is superseded by MERL TR2004-040, available at http://www.merl.com/papers/TR2004-040/.The region graph method is the most general of these methods, and it subsumes all the other methods. Region graphs also... more

Fig. 1. A small factor graph representing the joint probability distribution p(#1,%2,%3,24) = $fa(w1, 2) fB(w2,03, 04) fo (wa).

Fig. 2. Anillustration of the definition of a region. Regions are sets of variable and factor nodes in a factor graph such that all variable nodes connected to any included factor nodes are included. Thus, the sets of nodes {1,2} and {B,C, 2,3, 4} could be regions, but {B, 3} could not be a region (since factor node B was included, variable nodes 2 and 4 must also be included.) has been described in the physics literature, and will therefore refer to such approximations as region-based approximations. We refer to the sub-class of approximations specifically gener- ated using the cluster variation method as Kikuchi approxima- tions. We begin by assuming that p(x) has the factor graph form of equation (1). We define a region R of a factor graph to be a set Vr of variable nodes and a set Fr of factor nodes, such thatif a factor node a belongs to Fr, all the variable nodes neighboring a are in Vy. We give examples of sets of nodes that could or could not be considered regions in figure 2. Note that the set FR may be empty, and that a factor a need not be included in Fp even if all its neighboring variable nodes are in Vp.

Fig. 3. A factor graph which we use to illustrate a variety of region-based free energy approximations. The Bethe method is a special case of the much more gen- eral region graph method. In appendices A and B, we discuss two other important methods that are also special cases of the region graph method: the junction graph method and the clus- ter variation method. In appendix C, we discuss in detail the relationship between the different methods.

Setting the derivative of the resulting Lagrangian Lpethe with respect to the beliefs b;(;) and b,(x,) equal to zero gives: Proof: We want to minimize the Bethe free energy, while in- sisting that all the beliefs b;(a;) and 6,(xq) are consistent. To this end, we add Lagrange multipliers \, («;) which enforce the constraint that Yixa\z; 2 a(Xa) = b;(x;) for every factor node a and all its neighboring variable nodes 7. We also need to add Lagrange multipliers to normalize the beliefs, but we do not clutter our equations with them, as their effects are automati- cally taken into account if we simply normalize our beliefs. ALYY 9 The fact that Leethe is bounded below implies that the BP lations always possess a fixed point (obtained at the global nimum of Lyethe). To our knowledge, this is the first proof the existence of BP fixed points for a general graph with ar- rary potentials. Of course, the existence of a fixed point does ‘imply that the BP algorithm will converge starting from ar- rary initial conditions.

Fig. 4. An example of a region graph. We have listed the counting number cr next to each region. Having defined region graphs, it is almost trivial to define a corresponding method for generating valid region-based free energy approximations. We simply create a region graph such that the vertices correspond to regions, with labels correspond- ing to the factor and variable nodes in a region, and we re- quire that every factor and variable node be contained in at least one region. We associate the counting numbers cr for regions directly with the counting numbers c, for the region graph, and the region graph free energy F'rg will be given by Fre = >i p¢rFr, where Fp is the free energy of the region R.

Fig. 5. An example of a graph of regions that is not a region graph because the sum of the counting numbers of regions containing variable node 5 is not one. the following reasons. First, to reiterate the comments we made about valid region-based free energy approximations, the con- dition that every factor node in the factor graph is counted once when we do the weighted sum over all regions ensures that the region graph average energy is exact if the region beliefs are ex- act; and the condition that every variable node is counted once ensures that the region graph entropy is a reasonable approxi- mation. The condition that the regions containing a particular variable node form a connected sub-graph will ensure that the marginal probability at any node is consistent irrespective of which region’s beliefs one uses to compute it. Empirically, we have found in limited experiments that if one attempts to run a GBP algorithm (as described below) on graphs that do not satisfy all the region graph conditions, the results will be poor. Anexample of a “false region graph” or graph of regions that does not satisfy the region graph conditions is shown in figure 5. The problem with this plausible-looking construction is that the sum of the counting numbers of the regions containing variable node 5 is zero, rather than one. We could modify this false region graph in a variety of ways to obtain a real region graph. For example, we could simply remove node 5 from the region {2,5}. The resulting region graph would be an example of a junction graph; see appendix A. Alternatively, we could add a region {5} which just contained variable node 5, and connect the regions {2,5}, {C,4,5}, {D,5,6}, and {5, 8} to it (the result of using the cluster variation method; see appendix B).

Fig. 7. A region graph with no cycles that has a corresponding region graph free energy approximation which is exact. Fig. 6. A factor graph that has a tree region graph shown in figure 7.

Here P(£) is the set of regions that are parents to region R, D(R) is the set of all regions that are descendants of region R, E(R) = RUD(R) is the set of all regions that are descendants of R and also region RF itself, and P(D)\E(R) is the set of all regions that are parents of region D except those that are also descendants of region R or region R. so ee To be more specific, in the parent-to-child algorithm, we only have one kind of message mp_;r(xR) from a parent region to a child region. Each region R has a belief bg(xp) given by

Fig. 8. A region graph used to illustrate the parent-to-child GBP algorithm. Note that we do not explicitly give the variable and factor node labels for each region, as for our purposes, we are only interested in the topology of the region graph.

Fig. 9. A factor graph that we will use for our detailed example of how to construct a GBP algorithm.

In words, this equation says that the belief at each region is a product of the local factors in that region, the messages from parents, and the messages into descendant regions from other parents who are not also descendants. Recall that in the parent; to-child algorithm, we only have one kind of message mp_,r(xr) from a parent region to a child region. Each region R has a belief be(xr) given by equation (44) which we re-write here:

For the decoding problem, the functions f;(x;) represent the likelihoods of the possible states of the bits, in light of the re- ceived block from the channel and the assumed channel model. Fig. 10. A region graph obtained for the factor graph of figure 9 using the cluster variation method.

In practice, it often helps convergence to only step the mes- sages part-way to their newly computed values. This simple heuristic can eliminate “over-shooting” problems.

Fig. 12. A junction graph for the factor graph shown in figure 3 generated using the Bethe method. Note the isomorphism between this junction graph and the original factor graph.

First, we show that the belief equations (E-4) hold. We have so that indeed bg (xp) is product of local potentials and incom- ing messages. Of course, we have one m message and one n message for every Lagrange multiplier A, so for these definitions to hold, we also need to have constraints relating the m’s and n’s. The constraints will be given by the definitions of the pseudo- messages and the relations between the messages and the pseudo-messages that we defined above. We want to show that these relations, as well as the two-way GBP belief equations previously defined, must hold. Tuming to the constraints, we have from the definition of n%_, p(Xp), that

Fig. 16. Anillustration of how one can take a region graph with some regions that have counting number zero, and obtain another region graph with no such regions but with an identical free energy. One first removes regions with a counting number of zero, and then directly connects any ancestor descendant pairs that have become disconnected. In this example, we form new direct connections between regions R and H and between regions B and H.

Fig. 17. A small illustrative region graph (see text). Note that region F' has counting number cy = 0. equal to zero, and when one implements it, one finds that the results at its fixed points are identical to those obtained when one surgically removes the cp = 0 regions. The reason that the algorithm still gives proper results, even though the above proof breaks down, is that the constraints that cannot be de- rived from the » constraints are actually not necessary- they all involve cr = 0 regions that do not contribute to the free energy in any case.

descriptionView Paper arrow_downwardDownload

Hierarchical Interpretation of Fractal Image Coding and Its Application to Fast Decoding

by Z. Baharav and

1993, Digital Signal Processing

The basics of a block oriented fractal image coder, are described. The output of the coder is an IFS(Iterated Function System) code, which describes the image as a fixed-point of a contractive transformation.A new hierarchical... more

descriptionView Paper arrow_downwardDownload

Gravity duals of Lifshitz-like fixed points

by Xiao liu

2008, Physical Review D

We find candidate macroscopic gravity duals for scale-invariant but non-Lorentz invariant fixed points, which do not have particle number as a conserved quantity. We compute two-point correlation functions which exhibit novel behavior... more

descriptionView Paper arrow_downwardDownload

Viscosity approximation methods for nonexpansive multimaps in Banach spaces

by Habtu Zegeye and

2010, Acta Mathematica Sinica, English Series

We prove strong convergence of the viscosity approximation process for nonexpansive nonself multimaps. Furthermore, an explicit iteration process which converges strongly to a fixed point of multimap T is constructed. It is worth... more

descriptionView Paper arrow_downwardDownload

Pathological Outcomes of Observational Learning

by Peter Sorensen

2000, Econometrica

This paper explores how Bayes-rational individuals learn sequentially from the discrete actions of others. Unlike earlier informational herding papers, we admit heterogeneous preferences. Not only may type-specific ‘herds’ eventually... more

FiGurE 1.—Expected payoff frontier. The diagram depicts the expected payoff of each of three actions as a function of the posterior belief r that the state is H. A rational individual simply chooses the action yielding the highest payoff. Here 2 is an insurance action, and 1 and 3 are extreme actions. With multiple types, we must introduce T labels for every action. Permuting &,, we order rational type t’s actions aj,...,ai,, by relative preference in state H, with aj, most preferred. So to be clear, if we order actions from least to most preferred by type ¢ in state H, then action m has rank = &' if m=a‘. By

FiGuRE 2.—Individual black box. Everyone bases his decision on both the public likelihood ratio / and his private belief p, resulting in his action choice aj, with chance w(a',,|L,/), and a likelihood ratio g(aj,,,1) to confront successors. Type ¢ takes action a/, if and only if his posterior likelihood m? I. —p)/p lies in the interval [/,, where /f,..., Th, partition [0,0].

FIGURE 3.—Signal densities. Graphs for the unbounded (left) and bounded (right) beliefs examples. Observe how, in the left panel, signals near 0 are very strongly in favor of state L. A. Unbounded Beliefs Example. Let the private signal o € (0,1) have state- contingent densities g“(a) =2o and g(a) = 2(1 — o )—as in the left panel of Figure 3. With a flat prior, the private belief p = p(o) then satisfies (1 — p)/p = g'(a)/g"(o) =(—o)/o by Bayes’ rule, and has the same conditional densi- ties fil= 2p and f*(p) = 20 — p), and c.d.f.’s F"(p) =p* and F'(p)=2p —p’. So supp(F) = [0,1], and private beliefs are unbounded; the cascade sets collapse to the extreme points, J, = {}, J, = {0}.

FIGURE 5.—Confounded learning. Based on our Bounded Beliefs Example, with AY = 4/5, u=v/2. In the left graph, the curves wU|H,/) and W(|L,/) cross at the confounding outcome [* = 8v/9, where no additional decisions are informative. At /*, 7/8 choose action 1, and strangely 7/8 lies outside the convex hull of A” and AY—e.g., in the introductory driving example, more than 70% of cars may take the high ramp in a confounding outcome. The right graph depicts continuation likelihood dynamics. For this example, we can argue that with positive chance, the process ¢/,, > tends to /* if it does not start in a cascade, i.e. in [0,2u/3] or [2v,~]. Since each likelihood continuation g(i,-) is increasing, if dynamics start in [2u/3,/*] or [/*,2v], they are forever trapped there. Assume /, € (2u/3,/*). Then <1, is a bounded martingale that tends to the end-points; therefore, the limit /,, places positive probability weight on both a limit cascade on / = 2u/3 and convergence

descriptionView Paper arrow_downwardDownload

Controlling chaos in the brain

by Duc Duong

1994, Nature

descriptionView Paper arrow_downwardDownload

Universality of data retrieval languages

by Alfred Aho

1979, Proceedings of the 6th ACM SIGACT-SIGPLAN symposium on Principles of programming languages - POPL '79

We consider the question of how powerful a relational query language should be and state two principles that we feel any query language should satisfy. We show that although relational algebra and relational calculus satisfy these... more

descriptionView Paper arrow_downwardDownload

Coupled fixed point theorems for nonlinear contractions without mixed monotone property

by Poom Kumam

a b s t r a c t We prove coupled coincidence and coupled common fixed point theorems for a mixed g-monotone mapping satisfying nonlinear contractions in partially ordered G-metric spaces. Presented theorems are generalizations of the very... more

descriptionView Paper arrow_downwardDownload

Fixed Points in M-Fuzzy Metric Spaces

by Jin Han Park

2007

Let (X, M, * ) be a complete fuzzy metric space with lim t→∞ M (x, y, t) = 1 for all x, y ∈ X and s * s ≥ s for all s ∈ [0, 1] and let A, B, S and T be self mappings of X. In this paper we give some conditions of which A, B, S and T have... more

descriptionView Paper arrow_downwardDownload

A fixed point theorem of the alternative, for contractions on a generalized complete metric space

by Rashwan Azooz

1968, Bulletin of The American Mathematical Society

descriptionView Paper arrow_downwardDownload

Supersymmetry and attractors

by Sergio Ferrara

1996, Physical Review D

We find a general principle which allows one to compute the area of the horizon of N=2 extremal black holes as an extremum of the central charge. One considers the ADM mass equal to the central charge as a function of electric and... more

descriptionView Paper arrow_downwardDownload

Bounding scalar operator dimensions in 4 D CFT

by Riccardo Rattazzi

2008, Journal of High Energy Physics

In an arbitrary unitary 4D CFT we consider a scalar operator φ, and the operator φ 2 defined as the lowest dimension scalar which appears in the OPE φ × φ with a nonzero coefficient. Using general considerations of OPE, conformal block... more

descriptionView Paper arrow_downwardDownload

Global Conservative Solutions of the Camassa–Holm Equation

by Alberto Bressan

2007, Archive for Rational Mechanics and Analysis - ARCH RATION MECH ANAL

This paper develops a new approach in the analysis of the Camassa–Holm equation. By introducing a new set of independent and dependent variables, the equation is transformed into a semilinear system, whose solutions are obtained as fixed... more

descriptionView Paper arrow_downwardDownload

Some notes on the paper “Cone metric spaces and fixed point theorems of contractive mappings”

by Rashwan Azooz

2008, Journal of Mathematical Analysis and …

Huang and Zhang reviewed cone metric spaces in 2007 [Huang Long-Guang, Zhang Xian, Cone metric spaces and fixed point theorems of contractive mappings, J. Math. Anal. Appl. 332 (2007) 1468-1476]. We shall prove that there are no normal... more

Some notes on the paper “Cone metric spaces and fixed point theorems of contractive mappings”

descriptionView Paper arrow_downwardDownload

DIFFUSION STRATEGIES FOR DISTRIBUTED KALMAN FILTERING: FORMULATION AND PERFORMANCE ANALYSIS

by Cassio Lopes

We consider the problem of distributed Kalman filtering, where a set of nodes are required to collectively estimate the state of a linear dynamic system from their individual measurements. Our focus is on diffusion strategies, where nodes... more

descriptionView Paper arrow_downwardDownload

Gradient calculations for dynamic recurrent neural networks: a survey

by Barak Pearlmutter

1995, IEEE Transactions on Neural Networks

Abstract| We survey learning algorithms for recurrent neural networks with hidden units, and put the various techniques into a common framework. We discuss xedpoint learning algorithms, namely recurrent backpropagation and deterministic... more

descriptionView Paper arrow_downwardDownload

Absolutely continuous invariant measures for maps with flat tops

by Michael Benedicks

1989, Publications Mathematiques De L Ihes

A random map is discrete-time dynamical system in which one of a number of transformations is randomly selected and applied at each iteration of the process. Usually the map τ k is chosen from a finite collection of maps with constant... more

descriptionView Paper arrow_downwardDownload

New Approximation Schemes for General Variational Inequalities

by Muhammad Noor

2000, Journal of Mathematical Analysis and Applications

In this paper, we suggest and consider a class of new three-step approximation schemes for general variational inequalities. Our results include Ishikawa and Mann iterations as special cases. We also study the convergence criteria of... more

descriptionView Paper arrow_downwardDownload

Global asymptotic stability of a general class of recurrent neural networks with time-varying delays

by jun wang

2003, IEEE Transactions on Circuits and Systems I-regular Papers

This paper investigates the absolute exponential stability of a general class of delayed neural networks, which require the activation functions to be partially Lipschitz continuous and monotone nondecreasing only, but not necessarily... more

descriptionView Paper arrow_downwardDownload

Some developments in general variational inequalities

by Muhammad Noor

2004, Applied Mathematics and Computation

General variational inequalities provide us with a unified, natural, novel and simple framework to study a wide class of equilibrium problems arising in pure and applied sciences. In this paper, we present a number of new and known... more

descriptionView Paper arrow_downwardDownload

The index theorem in QCD with a finite cut-off 1 Work supported in part by Schweizerischer Nationalfonds, by Iberdrola, Ciencia y Tecnologia, España and by the Ministerio de Educacion y Cultura, España. 1

by danny deleon

1998, Physics Letters B

The fixed point Dirac operator on the lattice has exact chiral zero modes on topologically non-trivial gauge field configurations independently whether these configurations are smooth, or coarse. The relation nL−nR=QFP, where nL (nR) is... more

descriptionView Paper arrow_downwardDownload

Existence results for fractional order functional differential equations with infinite delay

by Abdelghani Ouahab

2008, Journal of Mathematical Analysis and Applications

The Banach fixed point theorem and the nonlinear alternative of Leray-Schauder type are used to investigate the existence of solutions for fractional order functional and neutral functional differential equations with infinite delay.

descriptionView Paper arrow_downwardDownload

Stochastic dynamics of invasion and fixation

by Jorge Pacheco

2006, Physical Review E

We study evolutionary game dynamics in finite populations. We analyze an evolutionary process, which we call pairwise comparison, for which we adopt the ubiquitous Fermi distribution function from statistical mechanics. The inverse... more

descriptionView Paper arrow_downwardDownload

Novel local CFT and exact results on perturbations of N = 4 super Yang Mills from AdS dynamics

by Alberto Zaffaroni and

1998, Journal of High Energy Physics

We find new, local, non-supersymmetric conformal field theories obtained by relevant deformations of the N=4 super Yang Mills theory in the large N limit. We contruct interpolating supergravity solutions that naturally represent the flow... more

descriptionView Paper arrow_downwardDownload

Bilattices and the Semantics of Logic Programming

by Melvin Fitting

1991, The Journal of Logic and Algebraic Programming

Bilattices, due to M. Ginsberg, are a family of truth value spaces that allow elegantly for missing or conflicting information. The simplest example is Belnap's four-valued logic, based on classical two-valued logic. Among other examples... more

descriptionView Paper arrow_downwardDownload

Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order

by Xiao-gang Wen

2010

Two gapped quantum ground states in the same phase are connected by an adiabatic evolution which gives rise to a local unitary transformation that maps between the states. On the other hand, gapped ground states remain within the same... more

FIG. 1: (Color online) Energy spectrum of a gapped sys- tem as a function of a parameter s in the Hamiltonian. (a,b) For gapped system, a quantum phase transition can happen only when energy gap closes. (a) describes a first order quan- tum phase transition (caused by level crossing). (b) describes a continuous quantum phase transition which has a contin- uum of gapless excitations at the transition point. (c) and (d) cannot happen for generic states. A gapped system may have ground state degeneracy, where the energy splitting be- tween the ground states vanishes when system size L — co: limp—+oo € = 0. The energy gap A between ground and excited states on the other hand remains finite as LD > oo.

FIG. 2: (Color online) (a) A graphic representation of a quantum circuit, which is formed by (b) unitary operations on patches of finite size 1. The green shading represents a causal structure.

tanglement and simplify the wave function. In Ref. 58, the wave function renormalization for string-net states is generated by the following two basic moves

FIG. 6: (Color online) (a) A gLU transformation U acts in region A of a state |®), which reduces the degree freedom in region A to those contained only in the support space of |®) in region A. (b) U'U = P is a projector that does not change the state |®).

FIG. 7: A quantum state ona graph G. There are N+1 states on each edge which are labeled by | = 0,...,N. There are N, states on each vertex which are labeled by a = 1,..., Nu.

FIG. 9: A quantum state on a graph G. If the three edges of a vertex are in the states 2, 7, and k respectively, then the vertex has Nij~ states, labeled by a = 1,..., Nijz. Note the orientation of the edges are point towards to vertex. Also note that i + j > k runs anti-clockwise.

If we apply eqn. (18) twice, we reproduce eqn. (14). Thus eqn. (14) is not independent and can be dropped. Denm tho cranhin ranrodcantatinn (11) Wa nata that

two different paths; one contains two steps of local trans- formations and the other contains three steps of local transformations as described by eqn. (11). The two paths lead to the following relations between the wave func- tions: The consistence of the above two relations leads a condi- tion on the F’ tensor. on other part of graph, we obtain different wave func- tions W(a,8,x,m,n) which form a dimension Dj;xip+ space. In other words, Djjx1p* is the support dimension of the state ®g, on the region a, 8, v,m,n with bound- ary state i,7,k,l,p fixed (see the discussion in section VIIB). Since the number of choices of a, 8,x,m,n is Nijktp* = mn Nyim= Nemn«Ninp*; we have Dijkip« < Nijkips. Here we require a similar saturation condition as in (8):

The simplified second type renormalization can now be written as (since Djj« = 1) via the first type of renormalization steps (see Fig. 10), which are local unitary transformations. In the simplified

It is not clear if eqn. (48) and eqn. (49) will lead to new independent equations or not. In the following discus- sions, we will not include eqn. (48) and eqn. (49). We find that, at least for simple cases, the equations without eqn. (48) and eqn. (49) are enough to completely deter- mine the solutions.

Due to the relation (18), the different components of the tensor F; am are not independent. There are only four independent potentially non-zero components which are denoted as fo,...,f3: We note that FyJ?” in eqn. (11) relates wave functions on two graphs. In the above we have drawn the two related graphs after the F' tensor, where the first graph following F' corresponds to the graph on the left-hand side of eqn. (11) and the second graph corresponds to the graph on the right-hand side of eqn. (11). The doted line corresponds to the |0)-state on the link and the solid line corresponds to the |1)-state on the link. There are four potentially non-zero components in Pr , which are denoted by pg,...,p3:

The 7 = 1 fixed-point state corresponds to the Zz loop condensed state whose low energy effective field theory is the Zz gauge theory.**©° We call such a state, simply, the Zo state. The 7 = —1 fixed-point state corresponds to the double-semion state whose low energy effective field theory is the U(1)xU(1) Chern-Simons gauge theory®?° where 7 = +1. The above simplified equations can be solved exactly. We find two solutions parameterized by n=Hl:

Note that F’s described by f; and fs are the only F’s that change the number of |1)-links and the number of |1)|1)|1)-vertices. So we can use the local unitary trans- formation ef (OM +oMii1) to make f; and fs to be positive real numbers. (Here Mj is the total number of |1)-links and M,1, is the total number of |1)|1)|1)-vertices.) We also use the freedom of adjusting the total sign of Fy7;” to make Re(fo) > 0. Again, due to the relation (18), the different compo- nents of the tensor F;j”" are not independent. Now there are seven independent potentially non-zero components which are denoted as fo,...,f¢:

The fixed-point state corresponds to the N = 1 string-net condensed state°® whose low energy effective field theory is the doubled SO(3) Chern-Simons gauge theory.®°

EES RENAE RENEE nls inveietenemeerineneeunarin: PR Ieee gS STIRS RAE 0 SAMIAM Eee eee eneeone enn VGeRWNe neg meena vwwmtanen emcees eters the tensor F; a are not independent. There are eight independent potentially non-zero components which are denoted as fo,...,f7: The above N;;; satisfies eqn. (9), eqn. (30), and eqn. (47). Te ee A bee: woxlenktons TG hw Jefe: amon: -

FIG. 11: (Color online) Left: Tensor T’ representing a 2D quantum state on hexagonal lattice. 7 is the physical index, a, 8,y are inner indices. Right: a tensor product state where each vertex is associated with a tensor. The inner indices of the neighboring tensors connect according to the underlying hexagonal lattice.

FIG. 13: (Color online) F-move in the renormalization proce- dure: (1) combining double tensors T; and Tz on neighboring sites into a single double tensor T (2)Splitting double tensor T into tensor T (3) SVD decomposition of tensor T into tensors T, and Ty. FIG. 12: (Color online) Double tensor T represented as two layers of tensor T’ with the physical indices contracted. The gray layer is the lower layer.

FIG. 15: (Color online) P-move in the renormalization pro- cedure: (1) contracting three tensors that meet at a triangle Ta, I>, Tc to form a new tensor T™ on one site of the renor- malized hexagonal lattice. (2)constructing the double tensor T® from T™ so that we can start to do F-moves again. FIG. 14: Original hexagonal lattice (gray line) and renormal- ized lattice (black line) after F-move has been applied to the neighboring pairs of sites circled by dash line.

FIG. 17: (Color online) Renormalization procedure on square lattice part 1: (1) decomposing double tensor T into tensor T (2) SVD decomposition of T in two different directions, resulting in tensors T,, Ty, and T., Ta respectively.

FIG. 19: (Color online) Renormalization procedure on square lattice part 2: (1) combining four tensors that meet at a square into a single tensor (2) constructing a double tensor from it. FIG. 18: Original square lattice (gray line) and renormalized lattice (black line) after the operations in Fig. 17 has been applied. Physical indices of the tensors are not drawn here.

FIG. 20: Quantity X2/X1 obtained by taking the ratio of the contraction value of the double tensor in two different ways. X»2/Xy1 is invariant under change of scale, basis transforma- tion and corner double line structures of the double tensor and can be used to distinguish different fixed point tensors. For clarity, only one layer of the double tensor is shown. The other layer connects in exactly the same way.

[see eqns. (9, 30, 47 12, 18, 23, 33, 36)]. From the data (Nizks Fim 8 | pk-8) we can further find out the fixed- kln,x6 9~ 4 point wave function by solving the following equations for A‘,i =0,..., N: First, we find that the fixed-point local uni- tary transformations are described by the data (Nizrs Fim pliant that satisfy a

descriptionView Paper arrow_downwardDownload

Tensor-entanglement-filtering renormalization approach and symmetry-protected topological order

by Xiao-gang Wen

2009, Physical Review B

We study the renormalization group flow of the Lagrangian for statistical and quantum systems by representing their path integral in terms of a tensor network. Using a tensor-entanglementfiltering renormalization (TEFR) approach that... more

descriptionView Paper arrow_downwardDownload

Taming the infinite chase: Query answering under expressive relational constraints

by Michael Kifer

2008

A crucial task in Knowledge Representation is answering queries posed over a knowledge base, represented as a set of facts plus a set of rules. In this paper we address the problem of answering conjunctive queries posed over knowledge... more

Figure 2: Squid decomposition from Example 4 A possible squid decomposition is the following homomor- phism h defined as: h(V6) = V2, h(V4) = h(V5) = h(V7) = V3, and as the identity on the other variables. The result of the decomposition is the query shown in Figure 2, where its join graph is depicted, in order to distinguish the head from the tentacles.

descriptionView Paper arrow_downwardDownload

Non-perturbative formulas for central functions of supersymmetric gauge theories

by Daniel Anselmi

1998, Nuclear Physics B

For quantum field theories that flow between ultraviolet and infrared fixed points, central functions, defined from two-point correlators of the stress tensor and conserved currents, interpolate between central charges of the UV and IR... more

descriptionView Paper arrow_downwardDownload

Towards the F-theorem: $ \mathcal{N} = 2 $ field theories on the three-sphere

by Daniel Jafferis

2011, Journal of High Energy Physics

For 3-dimensional field theories with N = 2 supersymmetry the Euclidean path integrals on the three-sphere can be calculated using the method of localization; they reduce to certain matrix integrals that depend on the R-charges of the... more

descriptionView Paper arrow_downwardDownload

PACT XPP - A Self-Reconfigurable Data Processing Architecture

by Martin Vorbach

2003, The Journal of Supercomputing

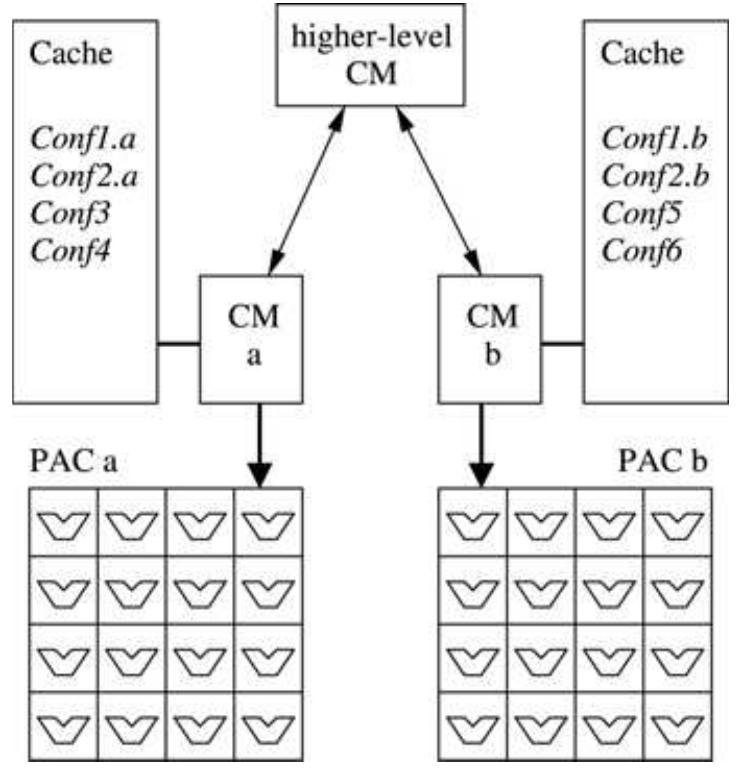
The eXtreme Processing Platform (XPPTM) is a new runtime-reconfigurable data processing architecture. It is based on a hierarchical array of coarsegrain, adaptive computing elements, and a packet-oriented communication network. The... more

Figure 1. A small configuration: matrix-matrix multiplication. Several of these configurations can be executed sequentially on an XPP'™ Core. Since each configuration processes long data streams, the reconfiguration overhead is amortized over many parallel operations. Results of computations are stored in distributed memories or FIFOs for use by subsequent configurations [10]. We call this programming paradigm configuration flow, as opposed to the instruction flow in a classical Von-Neumann architecture. The difference is illustrated in Figure 2. This programming paradigm is highly suited to computation-intensive applications since many of them can be separated into smaller, inherently parallel phases.

PACT XPP—A SELF-RECONFIGURABLE DATA PROCESSING ARCHITECTURE Figure 2. From instruction flow to configuration flow. The reconfiguration overhead is reduced to a minimum by caching configurations. Therefore, subsequent configurations are available instantly. The flow of configura- tions automatically synchronizes with the data streams.

PACT XPP—A SELF-RECONFIGURABLE DATA PROCESSING ARCHITECTURE igure 5. Parallel and independent configuration of multiple CMs.

Figure 6. Example of overlapped configuration and computation.

The complete Xpp™ Development Suite XDS [14] is available for NML programming. Figure 7 shows the design flow. The main component is the mapper xmap which compiles NML source files, places and routes the configurations, and

Figure 8. xvis screen shot. with the xsim and xvis tools in the suite, or directly executed on an XPP’™ device. Figure 8 shows a screen shot of xvis. For each clock cycle, all configured ALUs, registers and buses as well as all register values are visualized.

descriptionView Paper arrow_downwardDownload

Representation theory for high-rate multiple-antenna code design

by Amin Shokrollahi

2001, IEEE Transactions on Information Theory

Multiple antennas can greatly increase the data rate and reliability of a wireless communication link in a fading environment, but the practical success of using multiple antennas depends crucially on our ability to design high-rate... more

descriptionView Paper arrow_downwardDownload

Fixed point theorems for weakly contractive mappings on a metric space endowed with a graph

by Maria Samreen and

2014, Filomat

In this paper, we give some fixed point theorems for ϕ-weak contractive type mappings on complete G-metric space, which was given by Zaed and Sims [1]. Also a homotopy result is given.

descriptionView Paper arrow_downwardDownload

Topological feedback entropy and Nonlinear stabilization

by girish nair

2004, IEEE Transactions on Automatic Control

in consulting for both industry and government. He has taught a broad range of subjects in both mechanical and electrical engineering curricula. His research interests are in adaptive and learning systems, nonlinear control, and... more

descriptionView Paper arrow_downwardDownload

Alternating direction augmented Lagrangian methods for semidefinite programming

by Wotao Yin

2010, Mathematical Programming Computation

We present an alternating direction dual augmented Lagrangian method for solving semidefinite programming (SDP) problems in standard form. At each iteration, our basic algorithm minimizes the augmented Lagrangian function for the dual SDP... more

Fic. 4.1. Performance profiles of two variants of SDPAD for frequency assignment problems 4.2. The SDP relaxation of the maximum stable set problem. Given a graph G with edge set E, two SDPs relaxations of the maximum stable set problem are

number of iterations reached 10000. The minimum penalty parameter [yin is set to 0.1. All other parameters were set to their default values. Again, we did not run SDPNAL on our own computer but presented the results reported in Table 8 in [35] in Table 4.4. From this table, we can see that SDPADis faster than SDPNAL for achieving comparable lower bounds. Finally, performance plots for numerical results obtained using p = 1 and p = 1.6 are presented in Figures 4.4(a) and (b). When both the final duality gap and CPU time are considered, these plots again show that using a fixed step size of p = 1.6 is preferable to using a step size of p = 1. 5. Conclusion. In this paper, we presented alternating direction augmented Lagrangian methods for solving semidefinite programming (SDP) problems. At each inner iteration, the algorithm minimizes the dual

We first describe a result of the orthogonal decomposition.

Computational results on computing frequency assignment problems

Computational results on computing 6(G) Hence, the SDPNAL results in Tables 4.2 and 4.3 are taken from Tables 5 and 6 in [35]. Because the computer used to obtain the results in [35] has very similar performance characteristics to the computer that we used, the comparison presented in Tables 4.2 and 4.3 is meaningful. Specifically, when we run SDPNAL on smaller and easier problems, such as “fap01”-“fap12”, on our computer, the cpu time differed from those reported in [35] by an insignificant amount. From Table 4.2, we can see that SDPAD achieves approximately the same level of duality gap as SDPNAL on problems like “thetal02” to “thetal23”, “c-fat200-1” and “brock400-1”. Although SDPNAL is faster than SDPAD on problems like “hamming-10-2” and “G43” to “G47”, SDPAD is faster than SDPNAL on “2dc.512”. From Table 4.3, we can see that SDPAD is faster than SDPNAL on most problems except “hamming-9-5-6”, “hamming-10-2”, “1zc.1024” and “1zc.2048” while achieving almost the same level of duality gap. Finally, performance plots for numerical results obtained using p = 1 and p = 1.6 for computing 0(G) and 6,(G) are presented in Figures 4.2(a) and (b), and Figures A.3(a) and (b), respectively. When both the final duality gap and CPU time are considered, these plots again show that using a fixed step size of p = 1.6 is preferable to a step size of p = 1.

descriptionView Paper arrow_downwardDownload

Non-Fermi liquid behavior of electrons in the half-filled honeycomb lattice (A renormalization group approach)

by Francisco Guinea

1994, Nuclear Physics B

A system of electrons in the two-dimensional honeycomb lattice with Coulomb interactions is described by a renormalizable quantum field theory similar but not equal to QED 3 . Renormalization group techniques are used to investigate the... more

descriptionView Paper arrow_downwardDownload

Tripled fixed point theorems for contractive type mappings in partially ordered metric spaces

by cam huynh

2011, Nonlinear Analysis: Theory, Methods & Applications

Metric space Contractive type operator Tripled fixed point Existence and uniqueness a b s t r a c t

By using (2.4)-(2.6), it is a simple task to show that {x,}, {y,} and {z,} are Cauchy sequences. Indeed, form > n, one obtains where a = j + k-+1 < 1, which shows that {x,} is a Cauchy sequence. Similarly one can verify that {y,} and {z,} are also Cauchy sequences. Since X is a complete metric space, there exist x, y, z € X such that

Assuming that every triple of elements of X have either an upper bound or a lower bound in X, one can in fact show that ven the components of the tripled fixed points are equal, like in Example 1. The following theorem establishes this fact.

descriptionView Paper arrow_downwardDownload

Some Fixed Point Theorem for Mapping on Complete -Metric Spaces

by Zead Mustafa and

2008, Fixed Point Theory and Applications

We prove some fixed point results for mapping satisfying sufficient conditions on complete Gmetric space, also we showed that if the G-metric space X, G is symmetric, then the existence and uniqueness of these fixed point results follow... more

descriptionView Paper arrow_downwardDownload

The lightest Higgs boson mass in the Minimal Supersymmetric Standard Model

by Mariano Quirós

1995, Nuclear Physics B

We compute the upper bound on the mass of the lightest Higgs boson in the Minimal Supersymmetric Standard Model in a model-independent way, including leading (one-loop) and next-to-leading order (two-loop) radiative corrections. We find... more

descriptionView Paper arrow_downwardDownload

A review of the fractal image coding literature

by Brendt Wohlberg

1999, IEEE Transactions on Image Processing

Fractal image compression is a relatively recent technique based on the representation of an image by a contractive transform, on the space of images, for which the fixed point is close to the original image. This broad principle... more

descriptionView Paper arrow_downwardDownload

D-Branes at Singularities:A Bottom-Up Approach to the String Embedding of the Standard Model

by Fernando Quevedo

2000, Journal of High Energy Physics

We propose a bottom-up approach to the building of particle physics models from string theory. Our building blocks are Type II D-branes which we combine appropriately to reproduce desirable features of a particle theory model: 1)... more

descriptionView Paper arrow_downwardDownload

Covariance Structure Maximum-Likelihood Estimates in Compound Gaussian Noise: Existence and Algorithm Analysis

by Frédéric Pascal

2000, IEEE Transactions on Signal Processing

Recently, a new adaptive scheme [Conte et al. (1995), Gini (1997)] has been introduced for covariance structure matrix estimation in the context of adaptive radar detection under non-Gaussian noise. This latter has been modeled by... more

descriptionView Paper arrow_downwardDownload

Finite Groups with Fixed-Point-Free Automorphisms of Prime Order

by John Thompson

1959, Proceedings of The National Academy of Sciences

descriptionView Paper arrow_downwardDownload

Quantum critical transport, duality, and M theory

by Subir Sachdev

2007, Physical Review D

We consider charge transport properties of 2+1 dimensional conformal field theories at non-zero temperature. For theories with only Abelian U(1) charges, we describe the action of particle-vortex duality on the... more

descriptionView Paper arrow_downwardDownload

Offline Geometric Parameters for Automatic Signature Verification Using Fixed-Point Arithmetic

by jesus alonso

2005, IEEE Transactions on Pattern Analysis and Machine Intelligence

This paper presents a set of geometric signature features for offline automatic signature verification based on the description of the signature envelope and the interior stroke distribution in polar and Cartesian coordinates. The... more

descriptionView Paper arrow_downwardDownload

Toric Geometry, Sasaki–Einstein Manifolds and a New Infinite Class of AdS/CFT Duals

by James Sparks

2006, Communications in Mathematical Physics

Recently an infinite family of explicit Sasaki-Einstein metrics Y p,q on S 2 × S 3 has been discovered, where p and q are two coprime positive integers, with q < p. These give rise to a corresponding family of Calabi-Yau cones, which... more

descriptionView Paper arrow_downwardDownload

Fixed Point Theory

Related Topics