580 California St., Suite 400
San Francisco, CA, 94104
Key research themes
1. What are the structural characterizations and labeling constructions that guarantee harmonious and odd harmonious labelings in graphs?
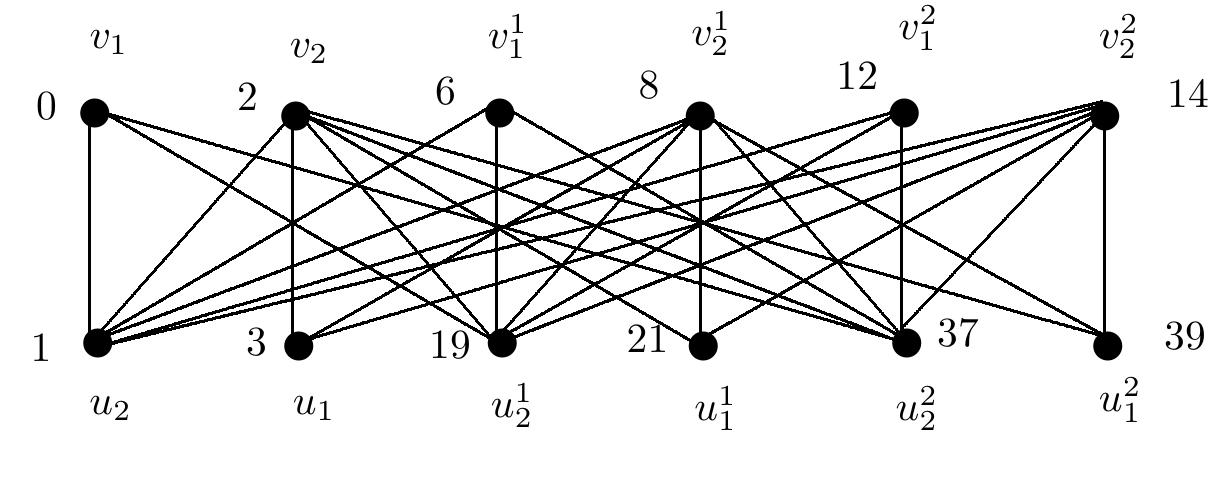
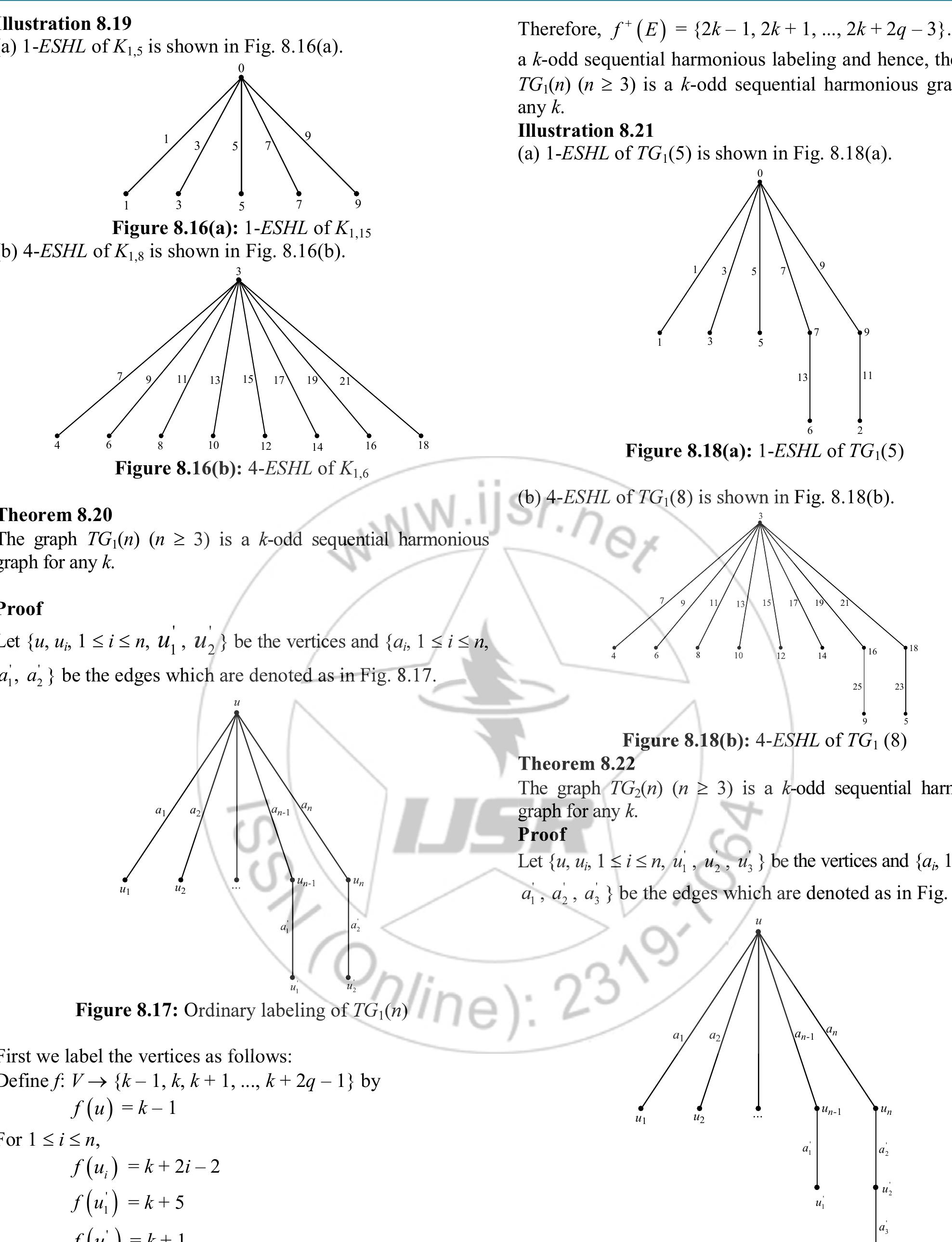
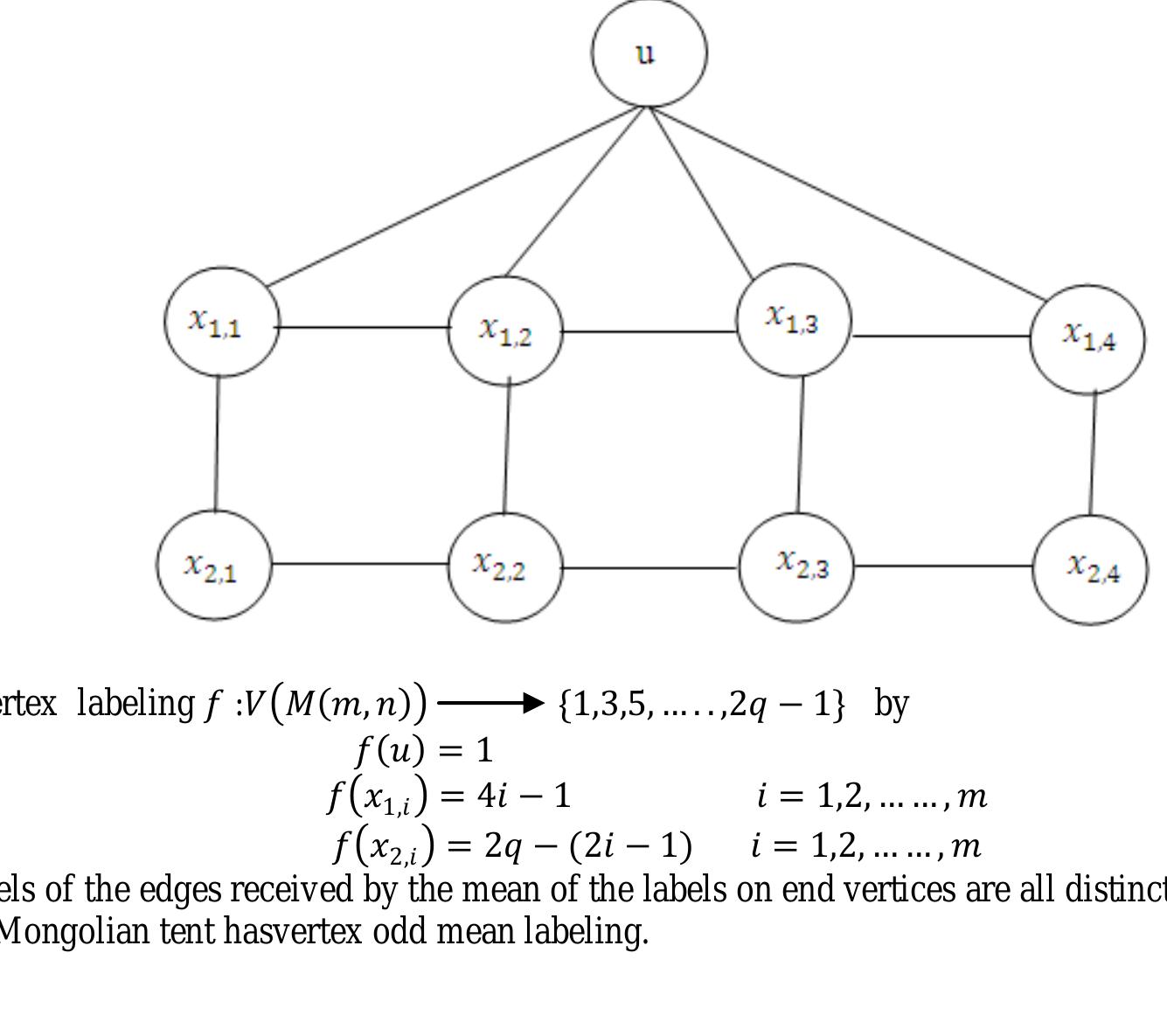
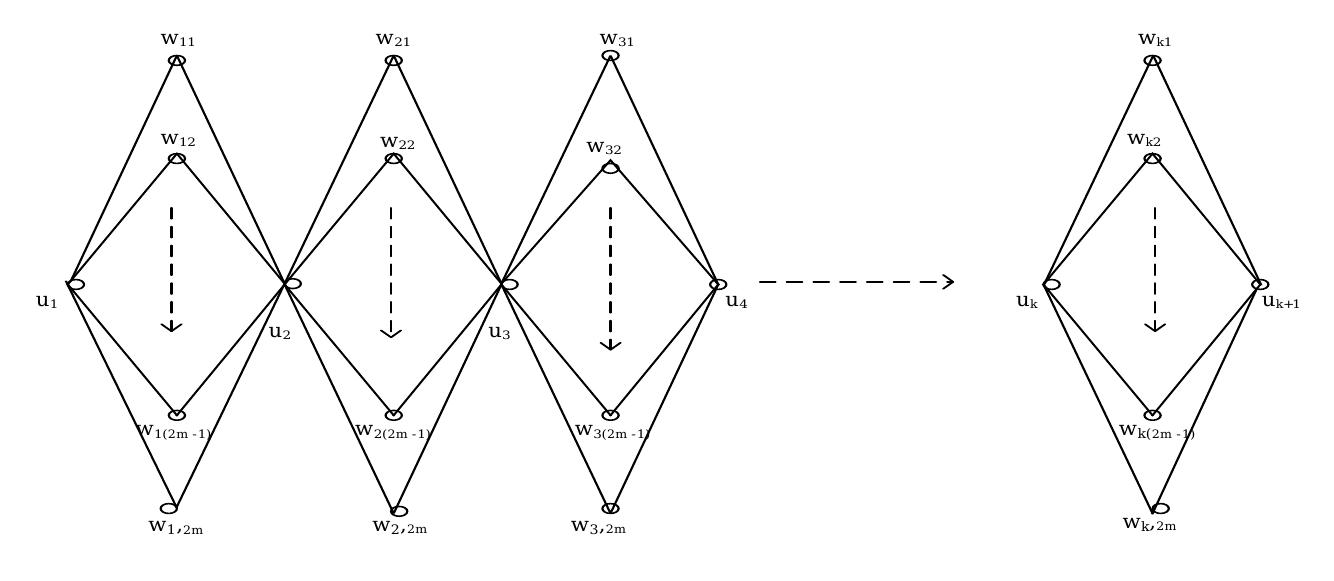
This theme investigates the existence and construction of harmonious and odd harmonious labelings for various classes of graphs, focusing on necessary and sufficient conditions for such labelings, explicit labeling functions for infinite families, and structural properties that influence harmoniousness. Harmonious labelings assign distinct sums modulo the number of edges to edges by vertex labels, with applications in coding and network communications. Odd harmonious labeling is a variation where vertex labels lie in a certain integer set inducing edge labels with specified parity properties. Understanding these characterizations is crucial both for combinatorial design and potential applications in communications and algebraic graph theory.
Key finding: Introduced a graph labeling problem defining a connected graph with n edges as harmonious if its vertices can be labeled with distinct integers mod n such that edge sums are distinct mod n, showed infinite families (odd... Read more
Key finding: Proved that certain graph constructions—m-shadow graphs on paths and complete bipartite graphs for all m ≥ 1, and n-splitting graphs on paths, stars, and symmetric products between paths and null graphs—are odd harmonious for... Read more
Key finding: Established that in any odd harmonious Eulerian graph the number of edges q satisfies q ≡ 0 or 2 (mod 4), gave counterexamples showing the converse is false, and constructed new infinite families of odd harmonious graphs... Read more
Key finding: Although primarily focused on spectral graph theory and graph energy, this study characterizes biregular trees and unicyclic biregular graphs with explicit degree parameters and structural constraints, providing conditions... Read more
Key finding: Analyzed spectral properties of graphs whose eigenvalue sets are closed under reciprocal operations and introduced graph operations (pendant join, splitting, double splitting, composition) that preserve spectral properties,... Read more
2. How do generalized adjacency matrices and spectral spreads characterize the structure and labeling properties of graphs related to harmoniousness?
This theme covers algebraic graph theory approaches examining spectral properties induced by generalized adjacency matrices (e.g., the A_α matrix interpolation between adjacency and Laplacian matrices) and measures such as generalized adjacency spread (difference between largest and smallest eigenvalues), connecting these spectral parameters to underlying graph structural properties relevant for harmonious labeling. Such spectral characterizations provide alternative methodologies and bounds on graph parameters influencing label uniqueness and injectivity conditions important in harmonious graph theory.
Key finding: Solved the problem characterizing graphs that minimize or maximize the spread of generalized adjacency matrices A_α for α ∈ [0,1], proving that for α ≥ 0.5 and sufficiently large maximum degree, the path graph attains minimum... Read more
Key finding: Established bounds for the maximum average connectivity attainable over all graph orientations, linked to underlying structural graph classes (e.g., cubic 3-connected, minimally 2-connected), thus connecting combinatorial... Read more
Key finding: Introduced a hierarchy of graphs associated with groups (power, enhanced power, commuting graphs), modified by equivalence relations (equality, conjugacy, order), and analyzed conditions for graph equality and properties such... Read more
3. What algorithmic and applied clustering methodologies improve face recognition systems emphasizing robustness important in graph labeling contexts?
This theme addresses algorithmic approaches in applying clustering, specifically K-Medoids clustering using PAM, in the context of face recognition systems that require robustness to noise and outliers. Given that harmonious graph labelings often model communication channels and network robustness, methods that enhance clustering in data with noise provide applicable insights for practical labeling constructions and error-correcting code designs inspired by graph labels.
Key finding: Demonstrated the use of K-Medoids with PAM algorithm for unsupervised clustering in face recognition, highlighting increased robustness against noise and outliers compared to K-Means and other methods. These robustness... Read more