k-Odd Sequential Harmonious Labeling of Some Special Graphs
2017
Abstract
Abstract: Graham and Sloane [7] introduced the harmonious graphs and Singh & Varkey [8] introduced the odd sequential graphs. Gayathri & Hemalatha [2] introduced even sequential harmonious labeling of graphs. We studied even sequential harmonious labeling of trees in [3]. In [4], we have extended this notion to k-even sequential harmonious labeling graphs. It is further studied in [5]. k-even sequential harmonious labeling of some cycle related graphs are studied in [6 ]. Also, we have introduced k-odd sequential harmonious labeling of graphs in [5]. In this paper, we investigate k-odd sequential harmonious labeling of some graphs.
Key takeaways
AI
AI
- The paper introduces k-odd sequential harmonious labeling as a novel graph labeling technique.
- The study investigates k-odd sequential harmonious graphs, defined by specific labeling conditions.
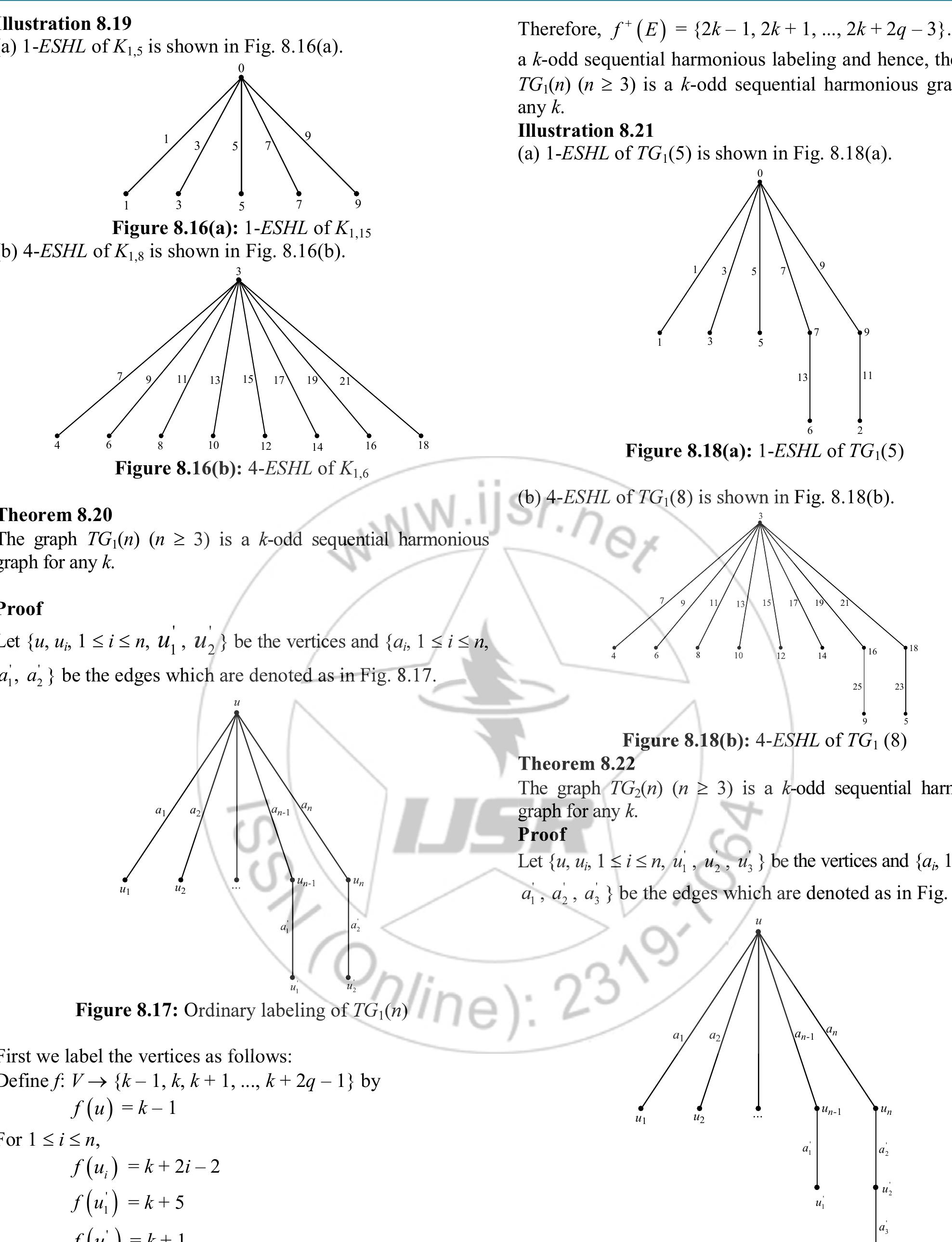
- Triangular snake graphs T_n are k-odd sequential harmonious for any positive integer k.
- Applications of graph labeling span various fields, including coding theory and circuit design.
- The paper builds on previous works regarding harmonious labeling techniques, particularly k-even and k-odd types.
References (12)
- J.A. Gallian, A dynamic survey of graph labeling -The Electronic Journal of Combinatorics 15(2008), #DS6.
- B. Gayathri and V. Hemalatha, Even sequential harmonious labeling of some graphs -Presented in national Conference hold at Govt. College for Women, Pudukkottai -28 & 29 th March 2008.
- B. Gayathri and D. Muthuramakrishnan, k-even sequential harmonious labeling of some tree related graphs, International Journal of Engineering Science, Advanced Computing and Bio-technology, Vol. 3, No. 2, April -June 2012, pp. 85-92.
- B. Gayathri and D. Muthuramakrishnan, Some results on k-even sequential harmonious labeling of graphs, Elixir Applied Mathematics, 47 (2012) 9054-9057.
- D. Muthuramakrishnan, Ph.D. Thesis, March 2013, k- even sequential harmonious labeling of graphs, Bharathidasan University, Tiruchirappalli-24.
- B. Gayathri and D. Muthuramakrishnan, k-even sequential harmonious labeling of some cycle related graphs, International Journal of Science and Research, 47 (2012) 9054-9057.
- R.L. Graham and N.J.A. Sloane, On addition bases and harmonious graphs, SIAM, J. Alg. Discrete Math., 1 (1980) 382-404.
- G.S. Singh and T.K.M. Varkey, On odd sequential and bisequential graphs, preprint.
- J.A. Gallian, A dynamic survey Electronic Journal of Combinatorics 15(2008), #DS6. of Combinatorics 15(2008), #DS6. of
- B. Gayathri and V. Hemalatha, Even sequential harmonious labeling of some graphs -Presented of some graphs -Presented of national Conference hold at Govt. College for Women, at Govt. College for Women, at Pudukkottai -28 & 29 th March
- B. Gayathri and D. Muthuramakrishnan, sequential harmonious labeling graphs, International Journal Advanced Computing and Bio-technology, Vol. April -June -June - 2012, pp. 85-92.
- B. Gayathri and D. Muthuramakrishnan, Some results k-even sequential harmonious labeling k-even sequential harmonious labeling k
 Dr. B Gayathri
Dr. B Gayathri