Derivations of abelian Lie algebra extensions

Derivations of abelian Lie algebra extensions

M. Barati
Department of Mathematics, Mashhad Branch, Islamic Azad University, Mashhad, Iran. mehdibarati1352@gmail.com

F. Saeedi
Department of Mathematics, Mashhad Branch, Islamic Azad University, Mashhad, Iran. saeedi@mshdiau.ac.ir

Received: 26.1.2019; accepted: 12.8.2019.
Abstract. Let $0 \rightarrow A \rightarrow L \rightarrow B \rightarrow 0$ be an abelian extension of Lie algebras. In this paper, we construct certain exact sequences which relate derivations with the Lie algebra cohomology group $H^{2}(B, A)$, and apply them to study extending derivations of $A$ and lifting derivations of $B$ to certain derivations of $L$.

Keywords: Derivation of Lie algebras; extensions of Lie algebras; second cohomology of Lie algebras; semidirect sum

MSC 2000 classification: Primary 17B40, 17B56; Secondary 18G60.

1 Motivation and preliminaries

Cohomology theories of various algebraic structures have been investigated by several authors. The most noteworthy are due to Hochschild, MacLance and Eckmann, Chevalley and Eilenberg, who developed the theory of cohomology groups of associative algebras, abstract groups, and Lie algebras respectively (see [3], [4], [5], and [10] for more information).
The theory of Lie algebras is one of the important parts of algebras. Many papers in the literature make an attempt to generalize the results on finite $p$ groups to the theory of Lie algebras. On the other hand there are same sporadic results for the Lie algebra that does not coincide with the results for groups. In fact, there are analogies between groups and Lie algebras, but the analogies are not completely identical and most of them should be checked carefully (see [2] and $[6]$ for examples).

The theory of group extensions and their interpretation in terms of cohomology is well known ( see [7] and [9] for example).

Over the years there has been an interest in studying the second cohomology of Lie algebras (see [2],[12]).

Let $A$ and $B$ be Lie algebras over a field $F$, where $A$ is abelian. We say that

^[1]

$A$ is a left $B$-module if there is a $F$-linear transformation $B \otimes A \rightarrow A$, written as $b \otimes a \mapsto b a$, such that

$$\left[b_{1}, b_{2}\right] a=b_{1}\left(b_{2} a\right)-b_{2}\left(b_{1} a\right) \quad \text { for all } b_{1}, b_{2} \in B \text { and } a \in A$$

Let $\operatorname{Der}(A)$ be the derivations of $A$ equipped with the Lie bracket

$$[f, g]=f g-g f \quad \text { for all } f, g \in \operatorname{Der}(A)$$

Then a left $B$-module structure on $A$ is equivalent to the existence of a Lie algebra homomorphism

$$B \rightarrow \operatorname{Der}(A)$$

Let $A$ and $B$ be Lie algebras. Then an extension of $B$ by $A$ is a short exact sequence of Lie algebras

$$0 \rightarrow A \xrightarrow{i} L \xrightarrow{\pi} B \rightarrow 0$$

where $L$ is a Lie algebra. Without loss of generality, we may assume that $i$ is the inclusion map, and we omit it from the notation. It follows from the exactness that $A$ is an ideal of $L$. If $A$ is abelian, then such an extension is called an abelian extension. This together with the Jacobi identity gives a left $L$-module structure on $A$ given by

$$x a:=[x, a] \quad \text { for } x \in L \text { and } a \in A$$

Let $t: B \rightarrow L$ be a section of $\pi$; that is, $t$ is a $F$-linear map such that $\pi t=0$. If $A$ is abelian, then this induces a left $B$-module structure on $A$ given by

$$b a:=[t(b), a] \quad \text { for } b \in B \text { and } a \in A$$

We denote the above $B$-module structure on $A$ by

$$\alpha: B \rightarrow \operatorname{Der}(A)$$

Our aim in this paper is to construct three exact sequences on derivation algebra of abelian Lie algebra extensions which relate derivations with cohomology of Lie algebras.
The sequences resemble well-known Wells exact sequence for group extensions which relate automorphisms with group cohomology (see [11] and [17] for more information).

Let $\operatorname{Der}(A), \operatorname{Der}(L)$, and $\operatorname{Der}(B)$ denote the derivations of $A, L$, and $B$, respectively.

Let $I$ and $J$ be two ideals of $L$. We introduce below some further notation to be used in this paper:

$$\begin{aligned} & \operatorname{Der}^{I}(L)=\{\gamma \in \operatorname{Der}(L) \mid \gamma(x) \in I \quad \text { for all } x \in L\} \\ & \operatorname{Der}_{J}(L)=\{\gamma \in \operatorname{Der}(L) \mid \gamma(x)=0 \quad \text { for all } x \in J\} \\ & \operatorname{Der}_{J}^{I}(L)=\operatorname{Der}^{I}(L) \cap \operatorname{Der}_{J}(L) \\ & \operatorname{Der}(L: I)=\{\gamma \in \operatorname{Der}(L) \mid \gamma(x) \in I \text { for all } x \in I\} \end{aligned}$$

Various aspect of derivations of Lie algebras has been investigated in the literature (see, for example, $[13,14,15]$ ).
Let $0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow 0$ be an abelian extension of Lie algebras over a field $F$, and let $t: B \rightarrow L$ be a section of $\pi$; so that every element of $L$ can be written uniquely as $t(b)+a$ for some $b \in B$ and $a \in A$.
Observe that a derivation $\gamma \in \operatorname{Der}(L: A)$ induces derivations $\theta \in \operatorname{Der}(A)$ and $\varphi \in \operatorname{Der}(B)$, given by $\theta(a)=\left.\gamma\right|_{A}(a)$ for all $a \in A$ and $\varphi(b)=\pi(\gamma(t(b)))$ for all $b \in B$. This gives a Lie homomorphism

$$\tau: \operatorname{Der}(L: A) \rightarrow \operatorname{Der}(A) \oplus \operatorname{Der}(B)$$

by setting

$$\tau(\gamma)=(\theta, \varphi)$$

We denote the restrictions of $\tau$ to $\operatorname{Der}^{A}(L)$ and $\operatorname{Der}_{A}(L)$ by $\tau_{1}$ and $\tau_{2}$, respectively.
Remark 1.1. To set notation, we briefly recall the definition of cohomology of Lie algebras.
Let $B$ be a Lie algebra, and let $A$ be a left $B$-module. For each $0 \leq k \leq \operatorname{dim} B$, define $C^{k}(B ; A)=\operatorname{Hom}\left(\Lambda^{k} B, A\right)$ and $\partial^{k}: C^{k}(B ; A) \longrightarrow C^{k+1}(B ; A)$ by

$$\begin{aligned} \partial^{k}(\nu)\left(b_{0}, \ldots, b_{k}\right)= & \sum_{i=0}^{k}(-1)^{i} b_{i} \nu\left(\ldots, \hat{b_{i}}, \ldots\right) \\ & +\sum_{0 \leq i<j \leq k}(-1)^{i+j} \nu\left(\left[b_{i}, b_{j}\right], \ldots, \hat{b_{i}}, \ldots, \hat{b_{j}}, \ldots\right) \end{aligned}$$

for all $\nu \in C^{k}(B ; A)$. It is straightforward to verify, using the Jacobi Identity and the $B$-action on $A$, that $\partial^{k+1} \partial^{k}=0$. Let $Z^{k}(B ; A)=\operatorname{ker}\left(\partial^{k}\right)$ be the group of $k$-cocycles, and let $B^{k}(B ; A)=\operatorname{image}\left(\partial^{k-1}\right)$ be the group of $k$-coboundaries. Then $H^{k}(B ; A)=Z^{k}(B ; A) / B^{k}(B ; A)$ is the $k t h$ Lie algebra cohomology group of $B$ with values in $A$.
Recently, Bardakov and Singh[1] gave an explicit description of a certain sequence for automorphisms of Lie algebras. We continue in the present work this

line of investigation for derivations of Lie algebras. In Section 2 we establish our exact sequences.

Theorem 1.2 (Main Theorem). Let $0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow 0$ be an abelian extension of Lie algebras. Then there exist the following three exact sequences

$$\begin{aligned} & 0 \rightarrow \operatorname{Der}_{A}^{A}(L) \rightarrow \operatorname{Der}^{A}(L) \xrightarrow{\tau_{1}} C_{1} \xrightarrow{\lambda_{1}} H^{2}(B ; A) \\ & 0 \rightarrow \operatorname{Der}_{A}^{A}(L) \rightarrow \operatorname{Der}_{A}(L) \xrightarrow{\tau_{2}} C_{2} \xrightarrow{\lambda_{2}} H^{2}(B ; A) \\ & 0 \rightarrow \operatorname{Der}_{A}^{A}(L) \rightarrow \operatorname{Der}(L: A) \xrightarrow{\tau} C_{\alpha} \xrightarrow{\lambda_{\varepsilon}} H^{2}(B ; A) \end{aligned}$$

The maps $\lambda_{1}, \lambda_{2}, \lambda_{\varepsilon}$ and notations $C_{1}, C_{2}$ and $C_{\alpha}$ will be defined in the next section.

2 Description of exact sequences

Let $\alpha: B \rightarrow \operatorname{Der}(A)$ be the $B$-module structure on $A$, and let $\operatorname{Ext}_{\alpha}(B, A)$ denote the set of equivalence classes of extensions of $B$ by $A$ inducing $\alpha$.
Let $\varepsilon: 0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow 0$ be an abelian extension of Lie algebras inducing $\alpha$.
We fix a section $t: B \rightarrow L$. For any two elements $b_{1}, b_{2} \in L$, we have

$$\pi\left(t\left[b_{1}, b_{2}\right]\right)=\left[b_{1}, b_{2}\right]=\left[\pi t\left(b_{1}\right), \pi t\left(b_{2}\right)\right]=\pi\left[t\left(b_{1}\right), t\left(b_{2}\right)\right]$$

Thus there exists a unique element, say $\delta\left(b_{1}, b_{2}\right) \in A$, such that $\delta\left(b_{1}, b_{2}\right)=$ $\left[t\left(b_{1}\right), t\left(b_{2}\right)\right]-t\left(\left[b_{1}, b_{2}\right]\right)$.
Observe that $\delta$ is a $F$-bilinear map from $B \oplus B$ to $A$ such that $\delta(b, b)=0$ for all $b \in B$.
Then it is easy to see that $\delta$ is a two-cocycle and two-coycles corresponding to different sections differ by a two-coboundary. Thus the map $[\varepsilon] \mapsto[\delta]$ gives a bijection $\operatorname{Ext}_{\alpha}(B, A) \leftrightarrow H^{2}(B ; A)$ (see [8, p. 238]).
In the following we present an important lemma used for proving theorems.
Lemma 2.1. Let $0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow 0$ be an abelian extension of Lie algebras over a field $F$. If $\gamma \in \operatorname{Der}(L: A)$, then there is a triplet $(\theta, \varphi, \chi) \in$ $\operatorname{Der}(A) \oplus \operatorname{Der}(B) \oplus \operatorname{Hom}(B, A)$ such that
(i) $\delta\left(b, \varphi\left(b^{\prime}\right)\right)+\delta\left(\varphi(b), b^{\prime}\right)-\theta\left(\delta\left(b, b^{\prime}\right)\right)=\left[t\left(b^{\prime}\right), \chi(b)\right]-\left[t(b), \chi\left(b^{\prime}\right)\right]+\chi\left(\left[b, b^{\prime}\right]\right)$
(ii) $\theta([t(b), a])=[t(\varphi(b)), a]+[t(b), \theta(a)]$ for all $a \in A$ and $b, b^{\prime} \in B$.

Conversely, if $(\theta, \varphi, \chi) \in \operatorname{Der}(A) \oplus \operatorname{Der}(B) \oplus \operatorname{Hom}(B, A)$ is a triplet satisfying equations $(i)$ and (ii), then, for all $a \in A$ and $b \in B, \gamma$ defined by

$$\gamma(t(b)+a)=t(\varphi(b))+\chi(b)+\theta(a)$$

is a derivation of $L$ lying in $\operatorname{Der}(L: A)$.
[Here $\delta$ is the two-cocycle corresponding to the extension $0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow$ $0, t: B \rightarrow L$ is a section of $\pi$, and $\operatorname{Hom}(B, A)$ is the group of all $F$-linear maps from $B$ to $A$ ].

Proof. Every derivation $\gamma \in \operatorname{Der}(L: A)$ determines a pair $(\theta, \varphi) \in \operatorname{Der}(A) \oplus$ $\operatorname{Der}(B)$ such that $\gamma$ restricts to $\theta$ on $A$ and induces $\varphi$ on $B$. For any $b \in B$, we have $\varphi(b)=\pi(\gamma(t(b)))$. Thus $\gamma(t(b))=t(\varphi(b))+\chi(b)$ for some element $\chi(b) \in A$. Since all the maps involved are $F$-linear, it follows that $\chi \in \operatorname{Hom}(B, A)$.
To prove $(i)$, let $b, b^{\prime} \in B$. We have

$$\delta\left(b, b^{\prime}\right)+t\left(\left[b, b^{\prime}\right]\right)=\left[t(b), t\left(b^{\prime}\right)\right]$$

By applying $\gamma$ and using the definition of $\chi$, we get

$$\theta\left(\delta\left(b, b^{\prime}\right)\right)+\chi\left(\left[b, b^{\prime}\right]\right)+t\left(\varphi\left(\left[b, b^{\prime}\right]\right)\right)=\left[\gamma(t(b)), t\left(b^{\prime}\right)\right]+\left[t(b), \gamma\left(t\left(b^{\prime}\right)\right)\right]$$

Since $\varphi$ is a derivation, we have

$$\begin{aligned} \theta\left(\delta\left(b, b^{\prime}\right)\right)+\chi\left(\left[b, b^{\prime}\right]\right)+ & t\left(\left[\varphi(b), b^{\prime}\right]\right)+t\left(\left[b, \varphi\left(b^{\prime}\right)\right]\right) \\ = & {\left[t(\varphi(b))+\chi(b), t\left(b^{\prime}\right)\right]+\left[t(b), t\left(\varphi\left(b^{\prime}\right)\right)+\chi\left(b^{\prime}\right)\right] } \\ = & \delta\left(\varphi(b), b^{\prime}\right)+t\left(\left[\varphi(b), b^{\prime}\right]\right)+\left[\chi(b), t\left(b^{\prime}\right)\right] \\ & +\delta\left(b, \varphi\left(b^{\prime}\right)\right)+t\left(\left[b, \varphi\left(b^{\prime}\right)\right]\right)+\left[t(b), \chi\left(b^{\prime}\right)\right] \end{aligned}$$

Thus we obtain condition $(i)$.
To derive condition (ii), we use the fact that $\gamma$ is a derivation. Let $b \in B, a \in A$. Then we have

$$\begin{aligned} \theta([t(b), a]) & =\gamma([t(b), a]) \\ & =[\gamma(t(b)), a]+[t(b), \gamma(a)] \\ & =[t(\varphi(b)+\chi(b), a]+[t(b), \theta(a)] \\ & =[t(\varphi(b), a]+[t(b), \theta(a)] \end{aligned}$$

Conversely, let $(\theta, \varphi, \chi) \in \operatorname{Der}(A) \oplus \operatorname{Der}(B) \oplus \operatorname{Hom}(B, A)$ be a triplet satisfying equations of $(i)$ and $(i i)$. To see $\gamma$ is a derivation of $L$, first we note that every

element of $L$ can be uniquely written as $l=t(b)+a$, where $b=\pi(l)$ and $a \in A$. Let $l_{1}=t\left(b_{1}\right)+a_{1}$ and $l_{2}=t\left(b_{2}\right)+a_{2}$, where $b_{1}, b_{2} \in B$ and $a_{1}, a_{2} \in A$. Then

$$\begin{aligned} (1) \gamma\left(\left[l_{1}, l_{2}\right]\right)= & \gamma\left(\left[t\left(b_{1}\right), t\left(b_{2}\right)\right]\right)+\gamma\left(\left[t\left(b_{1}\right), a_{2}\right]\right)+\gamma\left(\left[a_{1}, t\left(b_{2}\right)\right]\right) \\ = & \theta\left(\delta\left(b_{1}, b_{2}\right)\right)+\chi\left(\left[b_{1}, b_{2}\right]\right)+t\left(\varphi\left(\left[b_{1}, b_{2}\right]\right)\right) \\ & +\theta\left(\left[t\left(b_{1}\right), a_{2}\right]\right)-\theta\left(\left[t\left(b_{2}\right), a_{1}\right]\right) \\ = & \delta\left(b_{1}, \varphi\left(b_{2}\right)\right)+\delta\left(\varphi\left(b_{1}\right), b_{2}\right)+\left[t\left(b_{1}\right), \chi\left(b_{2}\right)\right] \\ & -\left[t\left(b_{2}\right), \chi\left(b_{1}\right)\right]+\left[t\left(\varphi\left(b_{1}\right)\right), a_{2}\right]+\left[t\left(b_{1}\right), \theta\left(a_{2}\right)\right] \\ & -\left[t\left(\varphi\left(b_{2}\right)\right), a_{1}\right]-\left[t\left(b_{2}\right), \theta\left(a_{1}\right)\right]+t\left[\varphi\left(b_{1}\right), b_{2}\right] \\ & +t\left[b_{1}, \varphi\left(b_{2}\right)\right] \end{aligned}$$

and

$$\begin{aligned} & {\left[\gamma\left(l_{1}\right), l_{2}\right]+\left[l_{1}, \gamma\left(l_{2}\right)\right]=\left[t\left(\varphi\left(b_{1}\right)\right)+\chi\left(b_{1}\right)+\theta\left(a_{1}\right), t\left(b_{2}\right)+a_{2}\right]} \\ & +\left[t\left(b_{1}\right)+a_{1}, t\left(\varphi\left(b_{2}\right)\right)+\chi\left(b_{2}\right)+\theta\left(a_{2}\right)\right] \\ & =\left[t\left(\varphi\left(b_{1}\right)\right), t\left(b_{2}\right)\right]+\left[t\left(\varphi\left(b_{1}\right)\right), a_{2}\right]+\left[\chi\left(b_{1}\right), t\left(b_{2}\right)\right] \\ & +\left[\theta\left(a_{1}\right), t\left(b_{2}\right)\right]+\left[t\left(b_{1}\right), t\left(\varphi\left(b_{2}\right)\right)\right]+\left[t\left(b_{1}\right), \chi\left(b_{2}\right)\right] \\ & +\left[t\left(b_{1}\right), \theta\left(a_{2}\right)\right]+\left[a_{1}, t\left(\varphi\left(b_{2}\right)\right)\right] \end{aligned}$$

By comparing (1) and (2), we have $\gamma \in \operatorname{Der}(L)$, and clearly, $\gamma(a)=\theta(a)$ for all $a \in A$. Therefore $\gamma \in \operatorname{Der}(L: A)$.

Remark 2.2. If $0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow 0$ is a central extension (that is $A \leq Z(L)$ ), then the action $B$ on $A$ becomes trivial, and therefore Lemma 2.1 takes the following simpler form which we will use in the proof of one of the next theorems.
Lemma 2.3. Let $0 \rightarrow A \rightarrow L \xrightarrow{\pi} B \rightarrow 0$ be a central extension of Lie algebras over a field $F$. If $\gamma \in \operatorname{Der}(L: A)$, then there is a triplet $(\theta, \varphi, \chi) \in$ $\operatorname{Der}(A) \oplus \operatorname{Der}(B) \oplus \operatorname{Hom}(B, A)$ such that, for all $b, b^{\prime} \in B$, the following condition is satisfied:

$$\delta\left(b, \varphi\left(b^{\prime}\right)\right)+\delta\left(\varphi(b), b^{\prime}\right)-\theta\left(\delta\left(b, b^{\prime}\right)\right)=\chi\left(\left[b, b^{\prime}\right]\right)$$

Conversely, if $(\theta, \varphi, \chi) \in \operatorname{Der}(A) \oplus \operatorname{Der}(B) \oplus \operatorname{Hom}(B, A)$ is a triplet satisfying above equation, then $\gamma$ defined by $\gamma(t(b)+a)=t(\varphi(b))+\chi(b)+\theta(a)$ is a derivation of $L$ lying in $\operatorname{Der}(L: A)$.
Remark 2.4. A pair $(\theta, \varphi) \in \operatorname{Der}(A) \oplus \operatorname{Der}(B)$ is called compatible if $\alpha \varphi(b)=$ $[\theta, \alpha(b)]$ for all $b \in B$. Equivalently, the following diagram commutes.

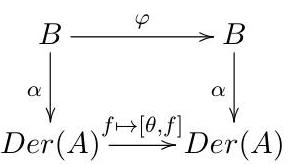
Note that $\alpha \varphi$ also gives a $B$-module structure on $A$. Then the compatibility condition is equivalent to saying that $\theta: A \rightarrow A$ is a $B$-module homomorphism from the $B$-module structure $\alpha$ to the $B$-module structure $\alpha \varphi$ on $A$.

Let $C_{\alpha}$ denote the Lie algebra of all compatible pairs; It is clear that $C_{\alpha}$ is a subalgebra of $\operatorname{Der}(A) \oplus \operatorname{Der}(B)$. Let

$$C_{1}=\left\{\theta \in \operatorname{Der}(A) \mid(\theta, 0) \in c_{\alpha}\right\}$$

and

$$C_{2}=\left\{\varphi \in \operatorname{Der}(B) \mid(0, \varphi) \in c_{\alpha}\right\}$$

For $\theta \in C_{1}$ and $\varphi \in C_{2}$, we define maps $k_{\theta}, k_{\varphi}, k_{\theta, \varphi}: B \oplus B \rightarrow A$ by setting, for $b, b^{\prime} \in B$

$$\begin{aligned} & k_{\theta}\left(b, b^{\prime}\right)=\theta\left(\delta\left(b, b^{\prime}\right)\right) \\ & k_{\varphi}\left(b, b^{\prime}\right)=\delta\left(\varphi(b), b^{\prime}\right)+\delta\left(b, \varphi\left(b^{\prime}\right)\right) \\ & k_{\theta, \varphi}\left(b, b^{\prime}\right)=\delta\left(\varphi(b), b^{\prime}\right)+\delta\left(b, \varphi\left(b^{\prime}\right)\right)-\theta\left(\delta\left(b, b^{\prime}\right)\right) \end{aligned}$$

Lemma 2.5. The maps $k_{\theta}, k_{\varphi}$, and $k_{\theta, \varphi}$ are two-cocycles.
Proof. For $b_{0}, b_{1}, b_{2} \in B$, by the fact that $\theta \in c_{1}$ and $\delta \in Z^{2}(B ; A)$, we have

ParseError: KaTeX parse error: Expected & or \\ or \cr or \end at position 1203: …], b_{0}\right)\̲r̲i̲g̲h̲t̲) \\ & =\theta(…

Hence $k_{\theta}$ is a two-cocycle.
We next show that $k_{\varphi}$ is a two-cocycle. For $b_{0}, b_{1}, b_{2} \in B$, we have

$$\begin{aligned} & {\left[t\left(b_{0}\right), k_{\varphi}\left(b_{1}, b_{2}\right)\right]-\left[t\left(b_{1}\right), k_{\varphi}\left(b_{0}, b_{2}\right)\right]+\left[t\left(b_{2}\right), k_{\varphi}\left(b_{0}, b_{1}\right)\right]-k_{\varphi}\left(\left[b_{0}, b_{1}\right], b_{2}\right)} \\ & +k_{\varphi}\left(\left[b_{0}, b_{2}\right], b_{1}\right)-k_{\varphi}\left(\left[b_{1}, b_{2}\right], b_{0}\right)=\left[t\left(b_{0}\right), \delta\left(\varphi\left(b_{1}\right), b_{2}\right)+\delta\left(b_{1}, \varphi\left(b_{2}\right)\right)\right] \\ & -\left[t\left(b_{1}\right), \delta\left(\varphi\left(b_{0}\right), b_{2}\right)+\delta\left(b_{0}, \varphi\left(b_{2}\right)\right)\right] \\ & +\left[t\left(b_{2}\right), \delta\left(\varphi\left(b_{0}\right), b_{1}\right)+\delta\left(b_{0}, \varphi\left(b_{1}\right)\right)\right] \\ & -\delta\left(\varphi\left(\left[b_{0}, b_{1}\right], b_{2}\right)-\delta\left(\left[b_{0}, b_{1}\right], \varphi\left(b_{2}\right)\right)\right. \\ & \left.+\delta\left(\varphi\left(\left[b_{0}, b_{2}\right]\right), b_{1}\right)\right)+\delta\left(\left[b_{0}, b_{2}\right], \varphi\left(b_{1}\right)\right) \end{aligned}$$

$$\begin{aligned} & -\delta\left(\varphi\left(\left[b_{1}, b_{2}\right]\right), b_{0}\right)-\delta\left(\left[b_{1}, b_{2}\right], \varphi\left(b_{0}\right)\right) \\ = & {\left[t\left(b_{0}\right), \delta\left(\varphi\left(b_{1}\right), b_{2}\right)\right]+\left[t\left(b_{0}\right), \delta\left(b_{1}, \varphi\left(b_{2}\right)\right)\right] } \\ & -\left[t\left(b_{1}\right), \delta\left(\varphi\left(b_{0}\right), b_{2}\right)\right]-\left[t\left(b_{1}\right), \delta\left(b_{0}, \varphi\left(b_{2}\right)\right]\right. \\ & +\left[t\left(b_{2}\right), \delta\left(\varphi\left(b_{0}\right), b_{1}\right)\right]+\left[t\left(b_{2}\right), \delta\left(b_{0}, \varphi\left(b_{1}\right)\right]\right. \\ & -\delta\left(\left[\varphi\left(b_{0}\right), b_{1}\right], b_{2}\right)-\delta\left(\left[b_{0}, \varphi\left(b_{1}\right)\right], b_{2}\right) \\ & +\delta\left(\left[b_{0}, b_{1}\right], \varphi\left(b_{2}\right)\right)+\delta\left(\left[\varphi\left(b_{0}\right), b_{2}\right], b_{1}\right) \\ & +\delta\left(\left[b_{0}, \varphi\left(b_{2}\right)\right], b_{1}\right)+\delta\left(\left[b_{0}, b_{2}\right], \varphi\left(b_{1}\right)\right) \\ & -\delta\left(\left[\varphi\left(b_{1}\right), b_{2}\right], b_{0}\right)-\delta\left(\left[b_{1}, \varphi\left(b_{2}\right)\right], b_{0}\right) \\ & -\delta\left(\left[b_{1}, b_{2}\right], \varphi\left(b_{0}\right)\right)=0 \end{aligned}$$

Note that $\varphi \in c_{2}$; therefore $[t(\varphi(b)), a]=0$ for $b \in B$ and $a \in A$.
Since $k_{\theta, \varphi}=k_{\theta}+k_{\varphi}$, we conclude that $k_{\theta, \varphi} \in Z^{2}(B ; A)$.
$\square \square \square$
Define $\lambda_{1}: C_{1} \rightarrow H^{2}(B ; A)$ by setting for $\theta \in C_{1}$,

$$\lambda_{1}(\theta)=\left[k_{\theta}\right], \quad \text { the cohomology class of } k_{\theta}$$

Similarly define $\lambda_{2}: C_{2} \rightarrow H^{2}(B ; A)$ by setting, for $\varphi \in C_{2}$,

$$\lambda_{2}(\varphi)=\left[k_{\varphi}\right], \quad \text { the cohomology class of } k_{\phi}$$

and define $\lambda_{\varepsilon}(\theta, \varphi): C_{\alpha} \rightarrow H^{2}(B ; A)$ by setting $\lambda_{\varepsilon}(\theta, \varphi)=\left[k_{\theta, \varphi}\right]$.
To justify these definitions, we need the following.
Lemma 2.6. The maps $\lambda_{1}, \lambda_{2}$, and $\lambda_{\varepsilon}$ are well defined.
Proof. To show that the maps $\lambda_{1}$ and $\lambda_{2}$ are well defined, we need to show that these maps are independent of the choice of sections. Let $t, t^{\prime}: B \rightarrow L$ be two sections. Then there exist maps $\delta, \delta^{\prime}: B \oplus B \rightarrow A$ such that, for $b_{1}, b_{2} \in B$,

$$\begin{aligned} \delta\left(b_{1}, b_{2}\right) & =\left[t\left(b_{1}\right), t\left(b_{2}\right)\right]-t\left(\left[b_{1}, b_{2}\right]\right) \\ \delta^{\prime}\left(b_{1}, b_{2}\right) & =\left[t^{\prime}\left(b_{1}\right), t^{\prime}\left(b_{2}\right)\right]-t^{\prime}\left(\left[b_{1}, b_{2}\right)\right] \end{aligned}$$

For $b \in B$, since $t(b)$ and $t^{\prime}(b)$ satisfy $\pi(t(b))=b=\pi\left(t^{\prime}(b)\right)$, there exists a unique element $k(b) \in A$ such that $t(b)=k(b)+t^{\prime}(b)$.
We thus have a map $k: B \rightarrow A$ by setting $k(b)=t(b)-t^{\prime}(b)$ for $b \in B$. For $b_{1}, b_{2} \in B, k\left(\left[b_{1}, b_{2}\right]\right)+t^{\prime}\left(\left[b_{1}, b_{2}\right]\right)=t\left(\left[b_{1}, b_{2}\right]\right)$. This gives

$$\begin{aligned} \delta\left(b_{1}, b_{2}\right)-\delta^{\prime}\left(b_{1}, b_{2}\right) & =\left[t\left(b_{1}\right), t\left(b_{2}\right)\right]-t\left(\left[b_{1}, b_{2}\right]\right)-\left[t^{\prime}\left(b_{1}\right), t^{\prime}\left(b_{2}\right)\right]+t^{\prime}\left(\left[b_{1}, b_{2}\right]\right) \\ & =\left[t\left(b_{1}\right), t\left(b_{2}\right)\right]-\left[t\left(b_{1}\right)-k\left(b_{1}\right), t\left(b_{2}\right)-k\left(b_{2}\right)\right]-k\left(\left[b_{1}, b_{2}\right]\right) \\ & =\left[t\left(b_{1}\right), k\left(b_{2}\right)\right]-\left[t\left(b_{2}\right), k\left(b_{1}\right)\right]-k\left(\left[b_{1}, b_{2}\right]\right) \in B^{2}(B ; A) \end{aligned}$$

Therefore

$$\begin{aligned} \theta\left(\delta\left(b_{1}, b_{2}\right)\right)-\theta\left(\delta^{\prime}\left(b_{1}, b_{2}\right)\right)= & {\left[t\left(b_{1}\right), \theta k\left(b_{2}\right)\right]-\left[t\left(b_{2}\right), \theta k\left(b_{1}\right)\right] } \\ & -\theta k\left(\left[b_{1}, b_{2}\right]\right)\left[t\left(b_{1}\right), k^{\prime}\left(b_{2}\right)\right] \\ & =\left[t\left(b_{2}\right), k^{\prime}\left(b_{1}\right)\right]-k^{\prime}\left(\left[b_{1}, b_{2}\right]\right) \in B^{2}(B ; A) \end{aligned}$$

where $k^{\prime}=\theta k$. This proves that $\lambda_{1}$ is independent of the choice of a section. Next we prove that $\lambda_{2}$ is well defined. It is sufficient to show that

$$\delta\left(\varphi\left(b_{1}\right), b_{2}\right)+\delta\left(b_{1}, \varphi\left(b_{2}\right)\right)-\delta^{\prime}\left(\varphi\left(b_{1}\right), b_{2}\right)-\delta^{\prime}\left(b_{1}, \varphi\left(b_{2}\right)\right) \in B^{2}(B ; A)$$

Proceed just as above and note that $\varphi \in C_{2}$ and $\varphi$ is derivation, we have

$$\begin{aligned} {\left[t\left(b_{1}\right), k \varphi\left(b_{2}\right)\right] } & -\left[t \varphi\left(b_{2}\right), k\left(b_{1}\right)\right]-k\left(\left[b_{1}, \varphi\left(b_{2}\right)\right]\right)+\left[t \varphi\left(b_{1}\right), k\left(b_{2}\right)\right]-\left[t\left(b_{2}\right), k \varphi\left(b_{1}\right)\right] \\ & -k\left(\left[\varphi\left(b_{2}\right), b_{1}\right]\right)=\left[t\left(b_{1}\right), k \varphi\left(b_{2}\right)\right]-\left[t\left(b_{2}\right), k \varphi\left(b_{1}\right)\right]-k \varphi\left(\left[b_{1}, b_{2}\right]\right) \end{aligned}$$

Putting $k \varphi=k^{\prime \prime}$

$$\left[t\left(b_{1}\right), k^{\prime \prime}\left(b_{2}\right)\right]-\left[t\left(b_{2}\right), k^{\prime \prime}\left(b_{1}\right)\right]-k^{\prime \prime}\left(\left[b_{1}, b_{2}\right]\right) \in B^{2}(B ; A)$$

This proves that $\lambda_{2}$ is also independent of the choice of a section.
Since $\lambda_{1}$ and $\lambda_{2}$ are well defined, $\lambda_{\varepsilon}$ is well defined too, and the proof of the lemma is complete.

Note that the maps $\lambda_{1}$ and $\lambda_{2}$ are not homomorphisms of Lie algebra. We are now in position to prove the main theorem.

Proof of Main Theorem. Let $0 \rightarrow A \rightarrow L \xrightarrow{\sigma} B \rightarrow 0$ be an abelian extension. Clearly all the sequences (1.1), (1.2), and (1.3) are exact at the first two terms. To complete the proof it only remains to show the exactness at the third term of the respective sequences. First consider the sequence (1.1). We show that $\operatorname{Im} \tau_{1}=\operatorname{Ker} \lambda_{1}$. Let $\gamma \in \operatorname{Der}^{A}(L)$. Then $\theta \in C_{1}$, where $\theta$ is the restriction of $\gamma$ to $A$. Lemma 2.1 implies that, for $b_{1}, b_{2} \in B$,

$$k_{\theta}\left(b_{1}, b_{2}\right)=\theta\left(\delta\left(b_{1}, b_{2}\right)\right)=\left[t\left(b_{1}\right), \chi\left(b_{2}\right)\right]-\left[t\left(b_{2}\right), \chi\left(b_{1}\right)\right]-\chi\left(\left[b_{1}, b_{2}\right]\right) \in B^{2}(B ; A)$$