Academia.eduAcademia.edu
All Topics
Mathematics
Numerical Analysis
Discontinuous Galerkin Methods

Discontinuous Galerkin Methods

description353 papers
group557 followers
lightbulbAbout this topic
Discontinuous Galerkin Methods are numerical techniques used for solving differential equations, particularly in computational fluid dynamics and wave propagation. They combine features of finite element and finite volume methods, allowing for discontinuous approximations within elements, which enhances flexibility in handling complex geometries and varying solution behaviors.
lightbulbAbout this topic
Discontinuous Galerkin Methods are numerical techniques used for solving differential equations, particularly in computational fluid dynamics and wave propagation. They combine features of finite element and finite volume methods, allowing for discontinuous approximations within elements, which enhances flexibility in handling complex geometries and varying solution behaviors.

Key research themes

1. How can truncation error-driven p-adaptation improve the efficiency and accuracy of high-order discontinuous Galerkin methods for compressible flows?

This research area focuses on adaptive strategies for high-order discontinuous Galerkin (DG) methods based on estimates of truncation error, particularly leveraging τ-estimation procedures to guide polynomial order refinements (p-adaptation). The aim is to identify regions requiring enrichment of polynomial degree to optimize computational cost without sacrificing accuracy for compressible fluid dynamics problems including Euler and Navier-Stokes equations. These methods accommodate anisotropic and spatially localized adaptation made feasible by DG's discontinuity allowance, which is critical for flows with varying smoothness and complex features like viscous boundary layers.

Adaptation strategies for high order discontinuous Galerkin methods based on Tau-estimation
by Esteban Ferrer and 
1 more
Gonzalo Rubio

2016, Journal of Computational Physics

Key finding: The paper develops three p-adaptation strategies (a posteriori, quasi-a priori, and quasi-a priori corrected) based on local truncation error approximations via τ-estimation, enabling identification of mesh regions for... Read more
articleView PaperdownloadDownload
A high-order discontinuous Galerkin solver for flow simulations and multi-physics applications
by eusebio valero

2023, Computer Physics Communications

Key finding: Describes a high-order DG framework that includes anisotropic p-adaptation capabilities guided by feature-based and truncation error estimates, allowing local polynomial order refinement in complex geometries. The solver... Read more
articleView PaperdownloadDownload
A class of embedded discontinuous Galerkin methods for computational fluid dynamics
by Bernardo Cockburn

2024, Journal of Computational Physics

Key finding: Introduces embedded discontinuous Galerkin (EDG) methods derived from hybridizable DG (HDG) methods with polynomial degree k for flux and trace approximations reduced to smaller global spaces. Although EDG methods sacrifice... Read more
articleView PaperdownloadDownload
keyboard_arrow_downShow more

2. What innovations in stabilization and approximation enable the effective discretization of viscous and diffusion terms in discontinuous Galerkin methods applied to incompressible and compressible fluid problems?

This theme examines methodological advances addressing the discretization challenges of diffusion and viscous terms in DG methods for Navier-Stokes and Stokes flows, emphasizing stability, consistency, and convergence on arbitrary and polygonal meshes. It covers novel stabilization mechanisms such as interior penalty methods (symmetric, nonsymmetric, incomplete), hybridized DG approaches ensuring pressure robustness, and penalty terms enabling equal-order velocity-pressure approximations. These advances are critical for achieving accuracy, optimal convergence, and robustness in DG schemes for viscous flows requiring effective treatment of discontinuities at element interfaces.

A Discontinuous Galerkin Method Based on a Gas Kinetic Scheme for the Navier-Stokes Equations on Arbitrary Grids
by Hong Luo

2022

Key finding: This work addresses the key difficulty in DG discretization of diffusive terms in Navier-Stokes equations, proposing numerical flux approximations that accurately handle inter-element discontinuities. The method integrates... Read more
articleView PaperdownloadDownload
Stabilised hybrid discontinuous Galerkin methods for the Stokes problem with non-standard boundary conditions
by Michał Bosy

2022

Key finding: Develops a stabilised hybrid DG method using equal-order polynomial approximations for velocity and pressure spaces that do not satisfy the inf-sup condition, adding a mesh-dependent stabilisation term penalizing pressure to... Read more
articleView PaperdownloadDownload
A fully interior penalty discontinuous Galerkin method for variable density groundwater flow problems
by Ali Raeisi

2023, Computers & Fluids

Key finding: Introduces a unified interior penalty DG (IPDG) framework combining symmetric, nonlinear, and incomplete IPDG variants for tightly coupling flow and transport equations in variable density porous media flow. The schemes... Read more
articleView PaperdownloadDownload
A pressure robust staggered discontinuous Galerkin method for the Stokes equations
by Lina Zhao

2025, Computers & Mathematics with Applications

Key finding: Proposes a pressure robust staggered DG method on polygonal meshes approximating velocity and pressure with piecewise constants, using a divergence-preserving velocity reconstruction operator incorporated into the discrete... Read more
articleView PaperdownloadDownload
keyboard_arrow_downShow more

3. How do space-time and Trefftz discontinuous Galerkin methods enable stable, high-order accurate discretizations for hyperbolic wave propagation problems, including Maxwell and acoustic wave equations?

This research focuses on discontinuous Galerkin methods that discretize both space and time simultaneously to solve hyperbolic wave problems, leveraging Trefftz functions (local solutions to the PDE) to reduce degrees of freedom and achieve improved accuracy and stability. With special attention to numerical flux definitions and inner product stabilizations, these methods provide fully implicit or explicit time-marching schemes without CFL restrictions, supporting unstructured meshes, local refinement, and hp-adaptivity. The approaches are applicable to Maxwell's equations, scalar wave equations, and elastic/acoustic wave propagation, offering superior convergence and error control compared to non-Trefftz or classical DG schemes.

A Space-Time Interior Penalty Discontinuous Galerkin Method for the Wave Equation
by Poorvi Shukla

2022, Communications on Applied Mathematics and Computation

Key finding: Presents a high-order space-time interior penalty DG method with basis functions discontinuous in space and time, providing a stable and convergent formulation that achieves optimal accuracy on unstructured and locally... Read more
articleView PaperdownloadDownload
A priori error analysis of space-time Trefftz discontinuous Galerkin methods for wave problems
by Fritz Kretzschmar

2016

Key finding: Develops and analyzes a space-time Trefftz-DG method that uses test and trial functions solving the PDE locally within each space-time element, specifically applied to Maxwell's equations and scalar wave problems in 1D. The... Read more
articleView PaperdownloadDownload
Hybridized Discontinuous Galerkin Methods for Wave Propagation
by Sébastien Terrana

2019, Journal of Scientific Computing

Key finding: Reviews development of hybridizable and embedded DG methods tailored for implicit discretizations of wave propagation problems including fluids, solids, and electromagnetism. These methods reduce globally coupled degrees of... Read more
articleView PaperdownloadDownload
keyboard_arrow_downShow more

Related Topics

  • Higher Order Methods
  • Finite Element Methods
  • Iterative Methods
  • Model Order Reduction
  • High Performance Computing
  • Spectral element methods
  • Continuum Mechanics
  • Fluid structure interaction
  • Path Following Methods
  • Delamination Simulation

    • All papers in Discontinuous Galerkin Methods

    A high order Discontinuous Galerkin - Fourier incompressible 3D Navier-Stokes solver with rotating sliding meshes for simulating cross-flow turbines
    by Esteban Ferrer
    "This thesis details the development, verification and validation of an unsteady unstructured high order (≥ 3) h/p Discontinuous Galerkin - Fourier solver for the incompressible Navier-Stokes equations on static and rotating meshes in two... more
    descriptionView Paperarrow_downwardDownload
    Numerical Methods for Direct Numerical Simulation and Stability Analysis
    by Esteban Ferrer

    VKI LS 2014-05, von Karman Institute for Fluid Dynamics Ed.

    Figure 1: Overview of the continuous and the discrete approaches to compute linear stability analysis. U, U and U denote continuous vectors for the original flow, base flow and perturbation respectively. The super-script h denotes spatially discretised. F and F” are the continuous and discrete fluxes respectively (F? = (V- F)").
    in: <" aas” /aa The p-refinement strategy or the use of arbitrary polynomial order p used in each mesh element, is illustrated in Fig. 2. The figure shows a two-dimensional sinusoidal function projected onto each mesh element using three different polynomial orders (p = 1, 2 and 3). It can be seen that without refining the mesh (h), p-refinement can be used to better approximate the sinusoidal solution. This property is exploited in the h/p Spectral method (i.e. spectral type methods that allow mesh or/and polynomial refinement). This method, introduced to flow problems in Patera (1984) (see also the monograph Szab6 and Babuska (1991) for the introduction of the method in the context of structural mechanics), is a modification of the classical Finite Element method where the basis functions (typically piecewise linear in Finite Elements) are replaced by polynomials of arbitrary order that maintain continuity across elements. The capability to use high order polynomials allows high order spatial calculations on coarse meshes (with p-refinement). The overwhelming advantage of spectral type meth- ods over low order methods is that exponential or spectral convergence can be achieved. This means that, when the number of Degrees of Freedom (DoF) is doubled, the error in the solution decreases by at least a factor of two and not with a fixed factor as in low-order methods. High order methods provide fast convergence and low diffusion and dispersion errors (see Karniadakis and Sherwin (2005) and references herein) and they are very suitable for applications where numerical errors have to be minimised (such as flow stability studies). Si i | | ee ee: ee ee: Ln ee, a a ee i a: ee. ee: |e i ae os |e gd
    triangular mesh elements and p the polynomial order) for a two dimensional Poisson equation (i.e. —Au = 27?cos(rx)cos(ry)) using the discontinuous Galerkin solver of Ferrer and Willden (2011, 2012); Ferrer (2012). The figure shows the errors for four meshes with 32, 50, 98 and 128 triangular elements and polynomial orders p, ranging from 2 to 7 (shown in boxes). It can be seen that for an equal number of DoF, the p-refinement strategy on a coarse mesh leads to a more accurate solution than the h-refinement strategy. Alternatively, it can also be seen that to achieve a fixed level of accuracy a fewer number of DoF are required when a high order polynomial in a coarse mesh is set than when h-refinement is performed using a fixed polynomial order.
    Figure 4: Three-dimensional mapping for hexahedral elements. In addition, these methods consider a computational element EF; and a linear transfor- mation (mapping) from physical to computational space, e, = E,, x = X(&), as shown in Fig. 4. The computational domain F is normally an hexahedra whose sides have unit length. This enables a Gauss (or Gauss-Lobatto) distribution of nodes to be defined inside the reference element (see Canuto et al. (2007) for further details).
    Figure 5: Riemann problem at the element interface (Courtesy of D. Kopriva). In the Navier-Stokes equations, these fluxes can be differentiated into two components viscous and inviscid fluxes. Computation of inviscid fluxes requires taking into accoun the left and right values of the unknowns at each interface. Let us note that by takin: she average value of the unknows U at the interface (equivalent to a central scheme provides a numerically unstable scheme when the convective terms dominates and is onl: recommended at very low Reynolds numbers. For larger Re, an upwinding scheme shoul pe used instead. The most common way to introduce upwinding in the scheme is b solving the equivalent Riemann problem at the interface. The Riemann fluxes are th solution of a 1D-partial differential equations with different left and right values (see Fig 5).
    with W = P~'U and the system is now decoupled (following the modal assumption). nN n The explicit | Euler scheme is stable for y = |1 + A;At| < 1, for A; any eigenvalue of A. This condition can be deduced from Eq. (25) and ensures that the new solution converges with time W"t! = yW”. Eq. (25) shows that the implicit backward Euler scheme is stable if x = |1 — \;At| > 1 since then yxW"*! = W” and W converges. \ = AAt defines the numerical eigenvalue and hence the maximum allowed time step At that fulfills the previous inequalities. In addition, \ defines the area of the complex plane that defines the stability region as shown in Fig. 6. The left picture shows the circular region of stability for the explicit forward Euler scheme (white zone). For the implicit | the right of Fig. 6), the outer region of the circular region in white defines the stability region. The stability region depends on the numerical scheme and is one of the most important properties of any numerical scheme. Euler (depicted on A practical implementation of a numerical scheme requires that, for each eigenvalue of A with negative real part, \;At is located inside the stability region, thus each eigenvalue has its own maximum allowable temporal time step. Normally, the problem involves several eigenvalues and the most restrictive At is chosen in the computation. If a steady solution is sought, it is possible to define a (local) temporal time step (At;) for each eigenvalue such that each eigenmode advances at its own time-step. This procedure is normally know as local-time step. It can be shown that in this case, the original problem is equivalent to the following preconditioned system:
    Figure 7: Schematic of a supercritical Hopf bifurcation. The Strouhal number of the solution is shown as a function of the parameter. Will LULL LUO TOW tO LLI© Littlit CYCIS LOVULeselucdad DY \a)- Although not discussed here, the stability of a periodic solution can be obtained fol- lowing Floquet analysis (Schmid and Henningson (2001)). Complementary to standard stability problems, Floquet analysis considers time dependent base flows in which the Jacobian is a matrix with time periodic coefficients. This is the case of, for example, sec- ondary instabilities in transition to turbulence boundary layer flows, where the periodic base flow is obtained after the saturation of a primary Tollmien-Schlichting or cross flow instahbjlitv wave. The influence of the Reynolds number in the flow after a circular cylinder is a practical example where the critical parameter undergoes a Hopf bifurcation. Other examples can be found in the literature, for instance Wales et al. (2012) used continuation to compute solutions for high Reynolds flow past a NACA0012 aerofoil at mid to high (but subsonic) Mach numbers. In this work, the continuation method correctly predicts the angle of attack (using A = AoA) for which the flow undergoes transitions from stable to unstable. In addition to Hopf type bifurcations, other types exist (e.g. Turning Point, Pitchfork or Phase transition) and can be predicted using continuation methodologies. The coexis- fees. oes ee ee | ees aa ee) eee ede Lk a, etna alee wen coe od ee es ee aS ARK ARIS AR SAA Ses
    ALLL MAUL it Ul ULLU LNW BOYyYUavuIUtinvo OALLA UCVILUTILUGMUIVY IL LO ULL UD The solution of the NS equations around a circular cylinder shows several flow regim pending on the Reynolds number (exposed in Fig. 8). For very small values of Re (i. okes flows) no separation occurs. The separation appears firstly when the Reynol umber surpasses a value of Re = 5. For Reynolds numbers in the range of 5 to 46, a pe steady vortices appear in the wake. The length of this recirculation region increases wi e Reynolds. For Reynolds numbers between 46 and 200, the wake becomes unsteac osing its 2D symmetry and giving birth to a vortex street (usually known as von Karmé reet) behind the cylinder. The vortex shedding frequency increases with the Reynol umber. The wake remains two-dimensional up to Rex 188 (Williamson (1996)), whe ree dimensional instabilities develop. For Reynolds in the range of 188 and 300 tl ike is tri-dimensional and transition to turbulence (or a disorganized regime, dependit the author) begins in the wake. However, the boundary layer detachment is still lamine irther increase of the Reynolds number moves progressively the transition upstream fro e wake to the cylinder. When the Reynolds number is increased beyond Re > 4.5e e complete boundary layer becomes turbulent. These regimes are summarised in Fi After this phenomenological description of the various bifurcations and flow regimes, let us illustrate the various concepts using high order numerical computations. We start analysing several configurations near the critical Reynolds Re, = 46. All the computations have been performed using a compressible NS solver at Mach number equal to 0.1. This low compressible regime enables comparisons with incompressible results obtained in the literature; Norberg (2003); Williamson (1996); Giannetti and Luchini (2007). A circular computational mesh has been created to study the problem. The internal radius is set to
    0.5 and the external boundary is defined at 40 diameters, far enough to avoid boundary interferences. The mesh is composed by 12 elements in axial direction and 15 in radial, given a total of 180 domains which are uniformly distributed along the azimuthal angle and follows a potential law from the surface of the cylinder to the external boundary. Taking into account that the boundary layer thickness at Re ~ 50 is around 0.2 chords, the first element on the surface is selected to have a height of 0.1, thus completely immersed into the boundary layer of the cylinder. At each element, a high-order Chebyshev collocation mesh of order px = pz = 5 is defined, which gives 0.001 diameters height for the first node in the boundary layer. Since the solution at this Reynolds number is two-dimensional, a polynomial of py = 1 has been defined in the spanwise coordinate (to save computational resources). The surface of the cylinder is approximated at each element with a polynomial of the same degree to avoid loss of accuracy. A detail of the mesh in the vicinity to the cylinder is shown in Fig. 9. This configuration contains a total number of 4500 nodes. Four different steady solutions are computed at Re = 44, 46,48,50. In these cases, he solutions show the well known fixed pair of symmetric vortices, where the length of he recirculation region increases with the Reynolds number (Fig. 10). It is important to how that at Re = 50 two different solutions can be found; first, a steady although unsta- le solution is computed by continuing the steady branch. The solution is analogous to he previously obtained at lower Reynolds number with larger length of the recirculation egion. By introducing a small perturbation into the vertical velocity of this steady solu- ion, the flow turns periodic with the well-known Karman street and a Strouhal number f around St = 0.12 which coincides with the one observed by the experiments (Norberg
    Figure 10: Left: symmetric vortices for the circular flow at Reynolds number bellow the critical. Right: Recirculation region as a function of the Reynolds number.
    Figure 11: Karman street at Reynolds 50 for the cylinder flow.
    Figure 12: Computational mesh designed for the cylinder problem at Reynolds=40(
    Figure 13: 3D flow filed for the circular cylinder at Re=400. The solution shows two different regimes in the unsteady evolution of the flow. First, the flow shows the develop- ment of 3D instabilities (left), then and incipient vortex breakdown in the wake appears (right).
    Figure 14: Neutral stability curves obtained by linear stability theory at Mach number 0.3. The analyzed unstable TS-modes are also indicated. The unstable frequency w; = 1 (lower straight line of Fig. 14) is used in our exper- iment. According to linear stability theory, the TS-waves associated to this frequency The perturbation problem has been computed for a value of the Reynolds number equal to Re = 10°, and a Mach number of M = 0.3. A non-dimensional length of 0.0152 is taken in the computations. This length makes the Reynolds number equal to the Re = 1e5 for standard atmospheric conditions and a Mach number equal to 0.3.
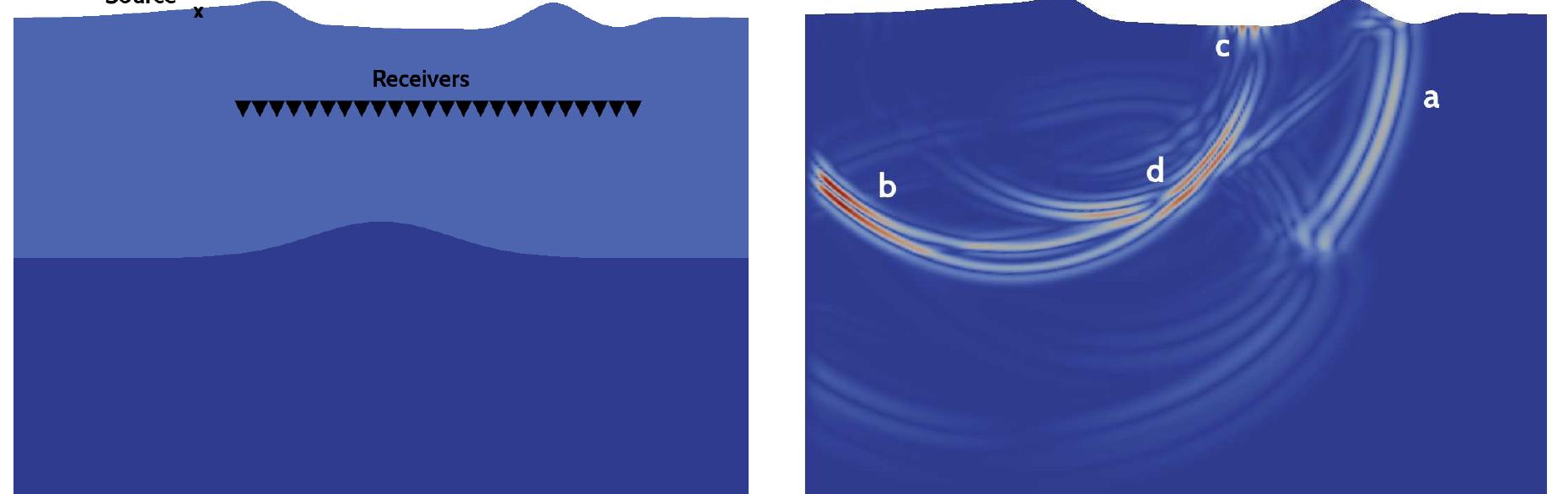
    Figure 15: Computational mesh for the TS evolution problem. The computational domain extends to (x, y, z) € (0, 30] x [0, 4] x [0, 1.5]). The mesh is uniform in the spanwise direction and follows a potential law in the direction normal to the wall. A total of 800 mesh elements are defined: 30 in the streamwise, 8 in the normal and 2 in the spanwise direction. Inside each element a polynomial of order px = py = pz = 5 is considered. Details of the mesh are shown in Fig. 15).
    sional features have not developed. Additionally, the comparison between the exponential growth rate of the NS computations and linear stability theory is shown (Fig. 16.right). As expected, for these almost parallel flows, no differences between both solutions are appreciated. Figure 16: Left: 3D view of the normal velocity perturbation. Top-Left: Tempora evolution for a selected point. Right: Numerical comparison between the spatial growtl rate between Navier-Stokes computations and linear stability theory.
    ‘igure 17: Structure of the matrix discretizing the BiGloblal operator in a single domain 3.2 Numerical Solution of the Eigenvalue Problem
    Figure 32: Isolines of the three velocity components of the leading secondary mode su- perimpose the spanwise velocity component of the primary disturbance.
    Figure 20: Real and imaginary parts of the 6 component of the eigenvector corresponding to the leading eigenmode of the Orr-Sommerfeld operator at critical conditions of plane channel flow. Result obtained using four subdomains, each resolved with polynomials of order 50. figuration with 50 nodes in each subdomain is used in the computations; the resulting eigenvalue problem is small enough to be solved by the direct QZ algorithm. In Fig. 20 the © component of the eigenvector corresponding to the leading eigenmode at critical conditions (Re = 5772, 22). Finally, in Table 5 the leading eigenvalue, obtained at critical conditions is show1 for different configurations of number of domains and number of points in each domain Both single-domain and multi-domain configurations provide an accurate solution as th: number of total points increased. | Equal total discretizations (e.g. 1 domain discretizec by 128 collocation points; 2 domains with 64 points each and 4 domains with 32 points offer solutions of equivalent quality, obtained within the same computational time. A: expected the single-domain approach is more accurate than the multi-domain one, thi can be explained by the always hig her order of the 1 domain polynomial compared wit] its equivalent in several domains, and the spectral convergence of this method.
    Figure 21: Upper row: Non-conforming (left) and conforming (right) meshes utilized for the L-cavity basic flow computations. Lower row: Positive (full- ne) and negative (dashed-line) isolines of u and @ at the near-critical Re = 650. Lower left: wu: levels shown are —0.4(0.015)1.0, Lower right: 0: levels shown are —0.63(0.015)0.32, method on a mapped single domain resolved by 256 x 256 nodes. A very good agreement between the two sets of results is observed in both quantities, while the small differences are attributed to the singular treatment of the lid-motion in Oosterlee et al. (1993) as opposed to the regularization (71) used presently.
    Figure 22: Comparison between present DNS results and Oosterlee et al. (1993) at Re=100. u(y) at x = 0.75 in left and v(x) at y = 0.75 in right.
    Figure 23: Left: Dependence of the amplification rate, Q,, on the spanwise wavenumber, @, in a range of Reynolds numbers around neutral stability. Right:Stability curves of the leading two eigenmodes.
    Figure 24: Positive (full-line) and negative (dashed-line) isolines of the amplitude func- tions pertaining to the leading eigenvector at Re = 650, 2 = 9.7. Left: @: levels shown are —0.024(0.002)0.024, Center: t: levels shown are —0. 038(0. 002)0.010, Right: w: levels shown are —0.022(0.002)0 : 018
    Figure 25: Positive (full-line) and negative (dashed-line) isolines of the t amplitude func- tions at Re = 650, = 9.7 obtained in the three cases, the parameters of which are summarized in Table 8. Superposed are the respective meshes used to discretize each of the eigenvector components. Levels shown are —0.02(0.002)0.02 The above discussion clarifies the differences seen in the plots of the eigenvectors, shown in Figs. 25. In the first of these, isolines of the wu disturbance velocity component obtained in Cases I, II-b and II are shown. Although knowledge of the converged re- sult ensures that that corresponding to Case I is the correct eigenvector, the differences with the other two results are imperceptible in this quantity. The small differences in the amplitude functions of velocity perturbations are exaggerated in the disturbance vor- ticity, in which (spectral) differentiation of the disturbance velocities is employed for the calculation of the vorticity components,
    Figure 26: Temporal evolution of the maximum of the spanwise velocity perturbatior obtained by direct numerical simulation The comparison is performed at Re = 900 and 6 = 10, where according to the global instability analysis only one unstable mode is presented. To reproduce this mode, the DNS solution is run until 150 non-dimensional time units. After a transient of around 50 time units a periodic behavior with exponential growth is achieved. In Fig. 26 the L.. of the spanwise velocity is monitored as a function of time. The exponential growth is obtained by a linear least squares fitting the maximum of each period, whereas the FFT analysis is performed to obtain the frequency. The obtained values are shown and compared with the stability analysis in Table 9, very good agreement is observed.
    saturated. The possibility of using the DMD technique with nonlinear solvers (i.e. no base flow required) should enable a wider range of applications. Finally, note that we can provide instability results from an existing nonlinear code without the necessity of writing a linearised version. The shape of the spanwise velocity component of the unstable eigenmode, obtained ising the Biglobal approach, was shown in Fig. 27.Left and can be compared to nonlinear ind linearised DNS simulations shown in Fig. 28.(a) and Fig. 28.(b). The shapes of he 3D instabilities that are visualised through velocity isocontours of w-velocity compare avourably to the BiGlobal mode. The visualisation of the DNS structures is possible in his case since the base flow has zero w-velocity component and there is only one unstable node present in the simulation. In addition, the three dimensional modes (only real art is shown) obtained using the DMD technique applied to nonlinear and linear DNS esults, Fig. 28.(c) and 28.(d), may be compared to the DNS structures and the BiGlobal igenmode (Fig. 27.Left) showing good agreement. Cyeantitatixa saeiwlae far tha dAxmamseal t~nfayvmathian 46 civmmmavidad in Tahla 1 Wa
    Figure 28: 3D global instability analysis using time-steppers at Reynolds 900 and non- dimensional spanwise length of 0.628, high order simulations use polynomial orders p=11 in the x-y plane and 64 Fourier planes in the z-direction: (a) Nonlinear DNS (DNS): 10 iso-surfaces of z velocity , (b) Linearised DNS (£DNS): 10 iso-surfaces of w-velocity, (c) MDNS+DMD: real part of the most unstable mode and (d) CDNS+DMD: real part of the most unstable mode.
    Figure 29: Infinite-swept-plate experiment. First a body-fixed system of coordinates: (x*,y, 27), where x* is the chordwise direction, z* is the spanwise direction and y is normal to the plate. (a*,y, 23) is a streamwise co- ordinate system, with x% oriented in the direction of the free-stream velocity. Finally the wave-aligned coordinate system (Xy, y, Zu), where ~ is the vortex wave angle, so phase velocity is in the x,-direction while zy is aligned with the constant phase lines. This is shown in Fig. 30.Left, and it is employed in the computations. *
    Figure 31: Left: Three components of the base primary state used in the Biglobal analysis. Right: Real and imaginary parts of the leading disturbances of the secondary flow Figure 30: Left: Swept plate:coordinate systems. Right: Saturated spanwise component of the stationary crossflow vortex for different chord values.
    It is interesting to compare the computational resources demand when using direct dense (using the QZ algorithm) versus an iterative sparse (using ARPACK) algorithm. Table 1 shows memory and CPU time requirements for recovery the solution of the inho- mogeneous case of (69) when f = exp(20(y — x — 1)). Besides the obvious conclusion that the sparse iterative approach is substantially more efficient than its dense direct counterpart, one notes that there is neither a memory nor a CPU time benefit in using multi-domain in combination with the dense direct approach. This is expected, since at the same level of discretization, the matrices stored and operated upon in the dense direct approach are of equivalent size. However, sparsity is well exploited when using the iterative sparse eigenvalue problem solver as the number of sub-domains in a multi-domain discretization increases. As an example, in order to obtain the converged result of (69) a 4 x 4 spectral multi-domain discretization requires O(400Mb) of memory
    Table 5: Leading eigenvalue of plane channel flow obtained at critical conditions, Re = 5772.22,a@ = 1.02056, using different combinations of number of subdomains, #dom, and number of collocation points in each subdomain, #pts. Reference result Q = (5.9(—10), 0.26400174)Orszag (1971). 4.2 The L-Shaped Cavity
    Table 11: Unstable secondary modes for Re = 890 and @ = 1.1. Finally, Figure 32 shows the iso-amplitudes plots for the velocity components of the leading secondary eigenmode, and the isolines for the spanwise primary velocity are su- perimposed.
    descriptionView Paperarrow_downwardDownload
    A high order Discontinuous Galerkin Finite Element solver for the incompressible Navier–Stokes equations
    by Richard Willden and 
    1 more
    Esteban Ferrer
    The paper presents an unsteady high order Discontinuous Galerkin (DG) solver that has been developed, verified and validated for the solution of the two-dimensional incompressible Navier-Stokes equations. A second order stiffly stable method... more
    Figure 1: Mapping from computational space to physical space. Within each element e/, the approximate solution, up, is expressed as a
    predicted by theoretical analysis [19]. ‘igure 2: L? relative error norm for the Poisson-Helmholtz equation for (a) p-refinement
    Figure 3: Time step refinement study for the unsteady Stokes equations at final time
    Table 1: Strouhal number for the square section cylinder at Re=100; experimental data and numerical results from the present DG implementation (for polynomial order k=5).
    Figure 4: (a) L* relative error norm and maximum pointwise error for p-refinement and
    descriptionView Paperarrow_downwardDownload
    On the ability of discontinuous Galerkin methods to simulate under-resolved turbulent flows
    by Pablo Fernandez
    We investigate the ability of discontinuous Galerkin (DG) methods to simulate under-resolved turbulent flows in large-eddy simulation. The role of the Riemann solver and the subgrid-scale model in the prediction of a variety of flow... more
    Figure 1: Time evolution of kinetic energy dissipation rate in the Taylor-Green vortex at Re = 1600 (left) and Re = © (right) for the Riemann solvers considered.
    Figure 2: Time evolution of numerical dissipation of kinetic energy, as defined in Eq. (4), in the Taylor-Green vortex at Re = 1600 (left) and Re = oo (right) for the Riemann solvers considered.
    Figure 3: One-dimensional kinetic energy spectrum in the Taylor-Green vortex at Re = 1600 and t = 8L/Vo (left), and Re = oo and t = 9 L/Vo (right) for the Riemann solvers considered.
    Figure 4: Time evolution of kinetic energy dissipation rate in the Taylor-Green vortex at Re = 1600 (left) and Re = o0 (right) for ILES, static Smagorinsky, dynamic Smagorinsky, WALE and Vreman LES.
    Figure 5: Time evolution of volume-averaged dynamic Smagorinsky constant in the Taylor-Green vortex. Note C; = 0.16 in static Smagorinsky [34].
    Figure 7: One-dimensional kinetic energy spectrum in the Taylor-Green vortex at Re = 1600 and t = 8L/Vo (left), and Re = co and t = 9L/Vo (right) for ILES, static Smagorinsky, dynamic Smagorinsky and Vreman. The WALE model led to nonlinear instability and the simulation breakdown at t = 4.59 L/Vo and 2.75 L/Vo in the viscous and inviscid cases, respectively. Figure 6: Snapshot of vorticity norm ||w|| £/Vo on the periodic plane x = —L7 of the viscous Taylor-Green vortex at t = 8L/Vo. Left to right: ILES, static Smagorinsky, dynamic Smagorinsky and Vreman. The WALE model led to nonlinear instability and the simulation breakdown at t © 4.59 L/Vo.
    Figure 8: Mean velocity profile in turbulent channel flow at Re!*"9*' = 182 (left) and 544 (right) for the Riemann solvers considered. The wall friction in the simulations is used to compute the near-wall velocity and length scales for non-dimensionalization.
    Figure 9: Reynolds stresses in turbulent channel flow at Re%*"9*' = 182 for the Riemann solvers considered. The wall friction in the simulations is used to compute the near-wall velocity and length scales for non-dimensionalization.
    Figure 10: Mean velocity profile in turbulent channel flow at Re'*"9*! = 182 for the SGS models considered. Inner (based on the wall friction in the simulation) and outer boundary layer scales are used for non-dimensionalization in the left and right figures, respectively.
    Figure 11: Mean velocity profile in turbulent channel flow at Re'*"9*' = 544 for the SGS models considered. Inner (based on the wall friction in the simulation) and outer boundary layer scales are used for non-dimensionalization in the left and right figures, respectively.
    Figure 12: Reynolds stresses in turbulent channel flow at Re’@"9*' = 182 for the SGS models considered. The wall friction in the simulations is used to compute the near-wall velocity and length scales for non-dimensionalization. The color legend is shown in Figures 10 and 11.
    Figure 14: Resolved eddy viscosity (top) and total eddy viscosity (bottom) in turbulent channel flow at Re%*"9 = 182 (left) and 544 (right) for the SGS models considered. The definition of these eddy viscosities is given in Eq. (7). The wall friction in the simulations is used to compute the near-wall velocity and length scales for non-dimensionalization. Figure 13: Dynamic Smagorinsky constant in turbulent channel flow at Re{“"9*' = 182 and 544. Note C, = 0.16 in static Smagorinsky [34].
    where : denotes the Frobenius inner product of two matrices. We finally define several inner products associated with these finite element spaces. In particular, given Ww, e vi, W,VeE oF and 7,¢ € Mt, we write where €} is a subset of €,. Different choices of €/ lead to different discretization methods within the hybridized DG family that have different properties in terms of accuracy, stability, and number of globally coupled unknowns [21, 61]. In particular, the HDG, EDG and IEDG methods are obtained by setting EF = 0, EF = & and EF = Ef, respectively.
    Table 2: Average absolute-value jump across elements on the periodic plane « = —Lm of the Taylor-Green vortex at Re = 1600 and t = 8L/V. Table 1: Average absolute-value jump across elements on the periodic plane « = —Lm of the Taylor-Green vortex at Re = 1600 andt =3L/V.
    Table 4: Average absolute-value jump across elements on the periodic plane « = —Lz of the Taylor-Green vortex at Re = oo andt =8L/Vo. Table 3: Average absolute-value jump across elements on the periodic plane x = —Lm of the Taylor-Green vortex at Re = oo and t=3L/VW.
    not exactly agree with the target Re, (denoted by Re!*"9**) if the resolution is not sufficiently fine to matck the wall stress in DNS. This will be the case at Re'“"9*' = 544 and, for some of the explicit models, also at 182. Table 5: Distance between high-order nodes (in wall units) for turbulent channel flow. Aysug denotes the average distance along the wall-normal direction. Ay, denotes the distance from the wall to the first high-order node along the wall-normal direction.
    Table 6: Values of Re£”5 computed from the wall friction in the LES simulations.
    descriptionView Paperarrow_downwardDownload
    Subgrid-scale modeling and implicit numerical dissipation in DG-based Large-Eddy Simulation
    by Pablo Fernandez
    Over the past few years, high-order discontinuous Galerkin (DG) methods for Large-Eddy Simulation (LES) have emerged as a promising approach to solve complex turbulent flows. However, despite the significant research investment, the... more
    descriptionView Paperarrow_downwardDownload
    Transient dynamics of beam trusses under impulse loads
    by Eric Savin

    2013, Yves Le Guennec - PhD Thesis, Ecole Centrale Paris

    This research is dedicated to the simulation of the transient response of beam trusses under impulse loads. The latter lead to the propagation of high-frequency waves in such built up structures. In the aerospace industry, that phenomenon... more
    descriptionView Paperarrow_downwardDownload
    Development and validation of a high order numerical solver for cross-flow turbine hydrodynamics
    by Esteban Ferrer
    We present a newly developed unstructured high order h/p Discontinuous Galerkin Finite Element solver for the computation of tidal turbine hydrodynamics. The solver allows for accurate flow solutions of the two dimensional incompressible... more
    descriptionView Paperarrow_downwardDownload
    MATLAB code for solving 2nd order homogeneous, constant coefficients BVPs via Galerkin’s Method over “n_e” elements
    by Dr. Redmond R . Shamshiri
    Galerkin’s method was used over "ne" elements in the entire domain [t1,t2] to numerically solve the 2nd order homogeneous, constant coefficients boundary value problem (BVP).
    descriptionView Paperarrow_downwardDownload
    High-Order Implicit Large-Eddy Simulation for Transitional Aerodynamics Flows
    by Pablo Fernandez
    This thesis presents a high-order Implicit Large-Eddy Simulation (ILES) approach for simulating transitional aerodynamic flows. The approach consists of a hybridized Discontinuous Galerkin (DG) method for the discretization of the... more
    descriptionView Paperarrow_downwardDownload
    An interior penalty stabilised incompressible Discontinuous Galerkin -Fourier solver for implicit Large Eddy Simulations
    by Esteban Ferrer

    2017, Journal of Computational Physics

    We present an implicit Large Eddy Simulation (iLES) h/p high order (≥ 2) unstructured Discontinuous Galerkin-Fourier solver with sliding meshes. The solver extends the laminar version of Ferrer & Willden, 2012 [36], to enable the... more
    descriptionView Paperarrow_downwardDownload
    Non-modal analysis of spectral element methods: Towards accurate and robust large-eddy simulations
    by Pablo Fernandez

    2018

    The use of high-fidelity flow simulations in conjunction with advanced numerical technologies, such as spectral element methods for large-eddy simulation, is still very limited in industry. One of the main reasons behind this, is the lack... more
    descriptionView Paperarrow_downwardDownload
    Entropy-stable hybridized discontinuous Galerkin methods for the compressible Euler and Navier-Stokes equations
    by Pablo Fernandez
    In the spirit of making high-order discontinuous Galerkin (DG) methods more competitive, researchers have developed the hybridized DG methods, a class of discontinuous Galerkin methods that generalizes the Hybridizable DG (HDG), the... more
    descriptionView Paperarrow_downwardDownload
    Blade-wake interactions in cross-flow turbines
    by Esteban Ferrer
    This paper presents analytical bounds for blade–wake interaction phenomenona occurring in rotating cross-flow turbines for wind and tidal energy generation (e.g. H-rotors, Darrieus or vertical axis). Limiting cases are derived for one... more
    descriptionView Paperarrow_downwardDownload
    A Reduced Order Model to Predict Transient Flows around Straight Bladed Vertical Axis Wind Turbines
    by Esteban Ferrer

    2018, Energies

    We develop a reduced order model to represent the complex flow behaviour around vertical axis wind turbines. First, we simulate vertical axis turbines using an accurate high order discontinuous Galerkin–Fourier Navier–Stokes Large Eddy... more
    descriptionView Paperarrow_downwardDownload
    Méthode de Galerkin discontinue appliquée à une équation de transport
    by Eric Savin

    2008, Bruno Berton - MSc Thesis, Université de Provence Aix-Marseille I

    descriptionView Paperarrow_downwardDownload
    A high order Discontinuous Galerkin - Fourier incompressible 3D Navier-Stokes solver with rotating sliding meshes
    by Richard Willden and 
    1 more
    Esteban Ferrer
    "We present the development of a sliding mesh capability for an unsteady high order (order>3) h/p Discontinuous Galerkin solver for the three-dimensional incompressible Navier-Stokes equations. A high order sliding mesh method is... more
    descriptionView Paperarrow_downwardDownload
    GPU Acceleration of High-Order Numerical Methods for Turbomachinery Flow
    by Mohamed H. Aissa

    2013, master thesis

    The aim of this work is to accelerate an existing two-dimensional explicit Euler solver implemented on a single CPU. The solver based on Discontinuous-Galerkin method for the spatial discretization is ported to run on a graphical... more
    Figure 2.1: Generic Diagram of the Single Instruction Single Data System (SISD) This category includes single-processor computers based on the common Von Neumann model illustrated in Figure 2.1. This is a serial processing hardware architecture.
    Figure 2.2: Generic Diagram of the Single Instruction Multiple Data System (SIMD), based on [1]
    Figure 2.3: Generic Diagram of the Multiple Instructions Multiple Data (MIMD),based on [1]
    The first class of shared-memory architecture (UMA) is also called symmetric multi- processor (SMP)/1][15]. The access of all memory locations occurs at the same speed, which causes the architecture to be symetric. This is indeed the simplest shared-memory architecture since all processors share the same connection (bus system) to the shared memory as shown in Figure 2.4. The bus system can not serve a large number of proces- sors, unless the memory access speed declines dramatically. The memory bandwidth is a limiting factor for UMA architecture. Figure 2.4: Generic Diagram of the Uniform Memory Access (UMA) Architecture
    Figure 2.5: Generic Diagram of the Non-Uniform Memory Access (NUMA) Architecture The non-uniform access is reflected in the access speed of the shared memory. Physically near shared-memory parts are accessed faster then other parts. With a higher number of processors the complexity of the NUMA architecture increases leading to important memory access delays known as latency. One strategy to minimize the memory traffic is to use a cache associated with every processor. The cache entries are kept coherent! through a protocol. This modified architecture is called cache coherent NUMA or ccNUMA. This modification leads however to a more complicated bus structure which raises the costs [15].
    Figure 2.6: Generic Diagram of the Distributed-Memory Architecture 2.1.3 Hybrid Architecture
    Figure 2.7: Generic Diagram of the Distributed-Shared Memory Architecture
    Figure 2.8: Generic Diagram of the GPU Cluster Architecture NVIDIA, the other major player in the GPU solution for HPC, has developed three architectures: Tesla, Fermi and Kepler (see table 2.1). The latter architecture was originally planned to be released late in 2011. However the release has been postponed until 2012 [15]. Like AMD, NVIDIA provides an SDK with CUDA as programming language (see 3.2).
    Figure 2.9: Summary Diagram of mentioned Architectures All the mentioned architectures are depicted in Figure 2.9. Flynn’s taxonomy was used to map the different architectures based on the data and instruction streams. The MIMD category was further split according to the memory organization into shared-memory, distributed memory and distributed shared-memory. The computational accelerators has been described with focus on the graphic processing unit (GPU). Colored ones represents used architecture in this work: uniform access memory system and graphic processing unit (see the implementation chapter 5).
    Figure 2.10: OpenMP fork-join execution model The OpenMP uses the fork-join model of parallel execution [20]. As illustrated in Figure 2.10 OpenMP program begins as a single thread of execution, called the initial thread. When any thread encounters a parallel region marked by the compiler directives, the thread forks additional threads creating a team of threads and becomes the master of the new team. The master thread and the new created threads execute the desired program part in parallel. There is an implicit synchronization barrier at the end of the parallel region. The threads wait until the full team reaches the barrier, and then they join back together. At that point the original or master thread continues until the next parallel region or the end of the program. The clause nowait deactivates the implicit synchronization through the barrier. This barrier forces all threads to wait for the slowest one among them.
    Figure 2.11: Generic Diagram of the Cluster of Nodes Architecture with MPI and OpenMP Models
    Figure 2.12: Diagram of the parallel programming design stages (based on [:
    Figure 2.13: Diagram of different speedups and processors numbers After all cells have calculated their temperatures, boundary area (blue and mauve right on Figure 2.13) has to be updated. This update is performed on a large number of cells. The Figure 2.13 illustrates a periodic boundary condition where the state at the end of the computation domain has to be copied at the end of the domain.
    Figure 2.15: Diagram of different speedups and processors numbers A program comprise a serial portion and a portion that could be parallelized. A parallel portion runs two times faster on two-processor systems as in one-processor system. The more processors are used the faster the parallel part will run. The serial part execution time remains untouched since it executes only on one processor. The Figure 2.15 illustrates the execution time of a program running on different numbers of processors. One fifth of the program is executed serially. The execution time of the serial part is constant and remains one fifth of the total execution time. The parallel execution time is inversely proportional to the number of processors. Four processors for instance are four time faster in running the parallel part but only two and half time faster than one processor running the entire program containing a serial portion of one fifth. The amount of performance benefit an application will realize by running on parallel systems depends entirely on the extent to which it can be parallelized [22]. G. Amdahl [23] was the first to model the performance expectation as follow :
    Figure 2.16: Expected speedup as a function of the parallel portion of a program running on 100 processors
    Figure 2.17: Expected speed up as a function of the number of processors for different parallel potions
    Figure 3.1: Comparison of the GPU and CPU architecture [3] The architecture of graphics computing units differs from the CPU architecture as the GPU was originally designed for graphics generation. Unlike the CPU most of the capacities are used for the computing. The CPU performs a multitude of different tasks, therefore most of the capabilities are invested on the memory caching and the control flow as shown in Figure 3.1. The GPU however contains more arithmetic logical units (ALU) dedicated for floating-point calculation. Graphical processing units are therefore taking more advantage from the Moore’s Law predicting the growth of the number of transistors on a chip.
    Block consists of 1 to 512 concurrent threads for GPUs with Tesla architecture [3]. Each thread has a unique thread ID (TID) starting with 0. Figure 3.2: illustration of the GPU device architecture [4]
    from all others. The order of running the blocks is therefore not relevant. If two blocks or more blocks executes in parallel the result remains the same. The programmer declares the number of threads of a block. The resource demand in form of registers and shared memory depends on the code being executed within a thread. When a streaming multiprocessor has enough resources for the block, the block of threads is created and every thread receives a thread ID (TID). Otherwise the block fails to start and the user is informed through a run-time error message (see Subsection 3.2.2). A streaming multiprocessor can start therefore at least one block of threads and up to eight concurrently [6]. The Tesla C1060 can thus execute from eight to sixty four blocks concurrently.
    Figure 3.4: Illustration of SIMT Warps Scheduling of two Blocks of Threads A SIMT streaming multiprocessor realizes full efficiency and performance when all 32 threads of a warp follow the same execution path [6]. If threads of a warp diverge via a data-dependent conditional branch, the warp serially executes each branch path taken as illustrated in Figure 3.5, disabling threads that are not on that path. When all paths complete, the threads reconverge to the original execution path. Thread divergence affects only threads within the same warp. Different warp can execute different code paths.
    Figure 3.5: Illustration of the serial execution of a divergent warp of threads For program correctness, programmers can essentially ignore SIMT execution attributes such as warps. They can achieve however substantial performance improvements by writing code that seldom requires threads in a warp to diverge.
    Figure 3.6: Overview of the CUDA device memory model|5] 3 Use of Graphics processing Units for Parallel Computation The API function cudaMalloc() allocates systematically the needed memory in the off-chir global memory. This type of memory is indeed 4GB large (see table A.1) and visible to all threads of all blocks but offers a slow access (latency). A read/write operation lasts between 400 and 800 clock cycles[3]. A variable lying in the global memory can be read and modified from any kernel or from the host by some API functions like cudaMemcpy The content of those variables exists during the whole application and remains untouched after one kernel is finished.
    Figure 4.1: One-dimensional Illustration of the inter-elements Discontinuity of the DG Global Solution The local DG approach of element-based basis functions leads to a discontinuous approximation solution q,. In each element interface there are two different solutions, one emerging from the element itself (q,,) and the other from the neighbor element (qp,_,, ). An illustration of the one-dimensional discontinuity of the local solutions q;,, is depicted in Figure 4.1.
    Table 4.1: RK Time Discretization Parameters where aj; and 3; are in Table 4.1 defined [35] Starting from the above described method a three-stage three-order exact Runge-Kutta method is used to integrate (4.13),cf. [29]:
    Figure 4.2: Illustration of a numerical domain subdivided in interior, Boundary and Ghost Elements
    Figure 5.1: Illustration of the four Steps of the Design Cycle for GPU Applications
    Figure 5.3: Illustration of the parallelization strategy
    Figure 5.4: Illustration of the parallelization of two function separated by a function running o: CPU
    Listing 5.1: Implementing of a CPU for-loop (left) on CUDA (right):
    Figure 5.5: Degree of freedom and integration Points for Surface and Volume Integral on a Triangle Element with first polynomial order (p=1) the same degree of freedom. A first polynomial-order triangle element is illustrated in Figure 5.5. For the volume integral three integration points situated at the center of every edge are used to compute the integral on every degree of freedom. The contributions of different integration points are computed in parallel. The contri- butions are added at the end of the integral and saved in the degrees of freedom. As shown in Figure 5.6 the kernel starts a set of threads, one per integration point. Every three threads are computing the integral on the same degree of freedom. The addition has to be performed serially otherwise a race condition emerges. Refer to Section 5.5 for the impact of this error on the final result. A full parallel kernel can be started after a partial parallel kernel as every kernel gets its new execution context? and parameter while starting.
    Figure 5.6: Illustration of the execution of full parallel (left) and partial parallel kernels (right
    Every element is an array of degrees of freedom and every degree of freedom is a structure with the conservative flow variables (p, pu, pv,e). For the graphics computational units the data has been rearranged in one-dimensional arrays. The access of the data is then performed using array index manipulation:
    5.4 Implemented Functions
    Figure 5.9: Flux calculation on Element Edges The race condition problem can be also hidden in the algorithm. The surface integral in this work, for instance, was implemented in the CPU in a way causing a hard-to-find race condition. The integral is calculated for every edge and added to the two neighbor elements on the edge as seen in Figure 5.9. Because the fluxes are computed in parallel, a case occurs that two or three different edges are writing in the same elements.
    Figure 5.10: Effect of the Race Condition on an acoustic pulse results: A race condition free output is shown on the left figure. The right figure is the output of an implementation with a race condition causing a noise in the results.
    Figure 6.1: Test-case:state at t=0 left, state at t=50 right To assess the potential of the DG method a benchmark problem (Category 4, Problem 1) from the first workshop on benchmark problems in computational aero-acoustics is solved [40]. This test case consists of the propagation of acoustic waves generated by a Gaussian pulse. Since the exact solution to the Linearized Euler Equations (LEEs) is available here, the results of simulations are used to study the accuracy of the spatial discretization scheme [29].
    Figure 6.4: Speedup high mesh resolution Figure 6.3: Speedup medium mesh resolution
    Figures 6.3 to 6.6 illustrate the reached speedups of multi-cores CPUs and the Tesla and Kepler GPUs with the one-core performance as reference. The performance measurement is done on medium and fine resolution (22300 and 99900 elements). The GPU makes a peak speedup of 66x in the medium resolution and only 50x peak performance in the fine resolution (see Figure 6.5 and 6.6).
    Figure 6.5: Speedup of a Kepler GPU with medium mesh resolution
    Figure 6.6: Speedup of a Kepler GPU with medium mesh resolution
    Listing A.1: Access of the Device Properties Property of the graphics processing unit device are saved in the structure cudaDeviceProp in the SDK header file (driver_types.h). The structure contains the device name, device computation power, warp size and many other device information. The listing A.1 shows the use of the API function cudaGetDeviceProperties, which accesses the device properties.
    on threads. ] Every thread runs separately a copy of the kernel. CUDA provides built-in variables? lis ted in table 3.1, which combined generate a thread identifier (tid) unique to every launched thread (line 3 Listing 3.2). The conditional construct surrounding the add operatio perform the n (line5-7) ensure through the condition (tid<N) that only needed threads add operation?. Threads are created with the kernel launch from the host. Listing 3.3 shows t call of the add function. It differs semantically from C/C++ function calls use of new execution configuration syntax (<<<,>>>). Between the inequa the user gives the number of blocks and the number of threads that should be These given parameters are saved then automatically in the built-in variables he kernel with the ity signs aunched gridDim and blockDim as listed in table 3.1. The kernel launch is asynchronous, which means the host can proceed other tasks on CPU directly after the kernel call before t computation is finished. he kernel
    kernel can call a device function, which run on the GPU device and can be called only within the device from a kernel or another device function. The declaration of this type of functions starts with a qualifier “___ device____” (See table 3.2). Kernels are executed in the device but callable only from the host. A kernel cannot return a value. A device function cannot call a kernel. A host function could be the main function or any other ANSI C conventional function running on the CPU host.
    To encounter the latency problem CUDA provides other type of memories that are not so large as the global memory and not overall visible, therefore faster accessible (see table 3.3).
    The solver routine is a function that uses the initial solution and the grid to solve the governing equations numerically and to produce a solution for a given time point t = tfinal. The solver, as illustrated in Algorithm 4.1, executes a series of iterations on the governing equations to proceed in time until the final time is reached. In every iteration a Runge-Kutta multiple step scheme (lines 3-6) is executed to solve the equations for one time step. The RK scheme requires a residual computation to update the physical solution (line 4). The eDisco program computes the residual for every time step using a set of functions solving the equation (4.9), as shown in Algorithm 4.2. One function computes the first term based on a surface integral S$? (line 1) and the second function adds a second term based on a volume integral H}. (line 2). The result is then multiplied with the inverse mass matrix M, i ,, (line 3). The final solution reached after a fixed amount of time stepping is stored in an output file.
    The surface integral and the volume integral are essential components of the DG solver and therefore described in the following Algorithms (4.3,4.4). The volume integral is a loop over all elements of the computational domain (lines 1-10). For every element the contributions of all integration points are calculated (lines 3-9) and added to the integral value of the element in every degree of freedom (line 9).
    The surface integral on the other hand runs over all the edges of the computational domain (line 1-9). For every edge the contributions of the integration points are calculated and added to the related degree of freedom of the element in the right (line 9) and the left (line 8) of the edge.
    Algorithm 4.4 Algorithm of the Volume Integral of The DG approach
    As important as the thread management the kernel itself has to be considered. A kerne could be fully parallel as illustrated in Figure 5.6. The kernel starts an amount! o threads, which run independently performing parallel computation and at the end save the results in separate memory positions. No memory conflict occurs. Some functions are however not fully parallel. The volume integral computes fluxes on integration points and save the results in every degree of freedom. This leads to thread conflicts since different threads compute different fluxes on different integration points and save their result in Nested loops are also a common parallelization pattern. The easiest way is to start two-dimensional blocks of threads as seen in Algorithm 5.1. The two indices blockIdx.x and blockIdx.y replace the two loops indexes i and j. The code could remain the same if no data dependency is identified. Synchronization may be required depending on the task. In comparison with the CPU algorithm 4.3 of the volume integral, the GPU algorithm replaces the two first loops covering the elements and the integration points. A third FOR-loop covering the degrees of freedom has been kept because of the high data dependency among the DOFs.
    6.1 Development and Test Environment
    Table 6.2 shows the estimated error Lzerror [42] of the numerical solution computed on the GPU. The error decreases with the increase of the mesh resolution from 8xh to 1xh. The estimated error decreases also with the increase of the polynomial order. Figure 6.2 shows the error estimate Lzerror for different polynomial order p plotted against the computational time. The error estimate presents a similar trend to the reference one achieving a certain accuracy level. The original CPU implementation generates the same error estimate plot with the aberration in the third polynomial order (cf. [29]).
    Table 6.3: Execution Time of the eDisco on GPU and different number of CPU cores combination
    Table 6.4: Speedup of the eDisco on GPU and different number of CPU cores combination
    Table 6.5: Speedup of the eDisco on different GPUs with the 16xcores Xeon workstation as reference and threads so much as a multiprocessors register and local memory can manage. The same configuration is run on the Kepler architecture. The programmer can take more advantage from the Kepler processor with the optimization of the started number of threads and blocks and also the use of the new feature as the L2 cache.
    On the other hand the execution time per DOF decreases with the increase of the mesh resolution. A better resolution is coupled with a higher number of elements. The increase of the elements number let the GPU compute more elements in parallel. The GPU starts a high number of threads and if the elements number is lower than the started threads some threads are inactive, which means a computation power portion is not used, some cores are idle.
    \ comparison with the error estimate of the numerical solution computed on 1xcore, xcores and 16xcores CPU and the Tesla GPU is shown in Table A.2. The error estimate f different architecture are from the same order of magnitude. The computation is done n single precision.
    Table A.3: Speedup of the GPU and different number of CPU processors (side bump, 5900 cells)
    Table A.4: Speedup of the GPU toward different number of CPU processors(side bump, 22300 cells)
    descriptionView Paperarrow_downwardDownload
    Development of a high order Discontinuous Galerkin Finite Element Solver
    by Esteban Ferrer
    An unsteady high order Discontinuous Galerkin (DG) code has been developed, verified and validated for the solution of the two-dimensional incompressible Navier-Stokes equations. A second order stiffly stable method has been used to... more
    Figure 1: Mapping from computational space to physical space.
    Figure 2: (a) Lz relative error norm for the Poisson equation and p-refinement; (b) Penalty parameter (c) influence on the Lz error norm for the Poisson equation, k=2.
    Figure 3: (a) 200 element mesh used to study the influence of the penalty parameter o on the solution of the Helmholtz equation; (b) Penalty parameter (a) influence on the L2 error norm for the Helmholtz equation of various wave numbers (a), SIPG flux and k= 2. showing optimal convergence for all polynomial orders. The meshes used, which are similar those used to solve the previous Poisson problem is of the type shown in Fig. 3.a. We again investigate the effect of the penalty parameter on the Lz error accuracy for the SIPG method and a fixed polynomial order k = 2 and 6 = 1. This time we vary the square of the wave number 0 < a < 10° and the penalty 18 < ao < 10* as shown in Fig. 3.b. It is interesting to analyse the behaviour of the method for large wave numbers because when considering the Helmholtz step in the splitting scheme, the wave number squared corresponds to a = yo/(v At), which can become large for small time steps. As
    Figure 4: Time step refinement study for the Stokes equations at final time=0.1, for various polynomia orders. (a) SIPG flux: Lz relative error norm for pressure, (b) SIPG flux: L relative error norm fo! velocity, (c) SIPG flux: D2 relative error norm for pressure with various penalisation (o), (d) SIPG flux Lz relative error norm for pressure with various penalisation (oc). Ly convergence obtained for time step refinement for the SIPG method for the pressure and the velocity respectively. For spatially well resolved simulations (k > 7), we obtain a convergence rate for the Lz relative error norm for pressure of 1.82 and 2.21 for velocity. These convergence rates are the same for all fluxes as long as the spatial discretisation is fine enough (reduced spatial error using either p or h refinement). The figures show that for all polynomial orders the scheme provides convergent solutions as long as the time step remains larger that a certain At,,;, which reduces as k increases. The overall error in the Ly norm seems to behave as O(At? + h**+!/At) with h representing the element size. In Fig. 4.c and Fig. 4.d, we depict the solution for k = 2 and 3 and two different values for the penalty 0. We observe an increase on the Ly norm (negative effect) for moderate
    Figure 5: (a) Lz relative error norm and (b) maximum pointwise error convergence rates for p-refinement and the Taylor Vortex problem, At = 0.001 and final time=0.1.
    Figure 6: DG solution: Vorticity contours —1 < w, < 1 for the square cylinder at Re=100, k= 7, SIPG flux. The unstructured triangular mesh is overlaid in the figure. and Sherwin! using the Spectral code Nektar!4 and by Shahbazi et al.!'§) where they compared their DG method to Darekar and Sherwin’s results. The domain boundaries anc effective blockage ratio (B = 2.3%) are identical to those used in the previous referencec studies. We use equal order P;(el)-P;(el) elements for velocity and pressure and a mest constituted of 836 triangular elements. We concentrate on the SIPG flux with 6 = 1 although the other fluxes have shown very similar results. Since in this case there is ¢ very significant variation of the element edge lengths (~ 0.01 — 10), we require an increas« in the penalty parameter o to ensure that the term race is large enough everywhere. A typical flowfield for Re = 100 is shown in Fig. 6. 4.1 Post processing forces- LIFT-DRAG
    Figure 7: Square section cylinder at Re=10: (a) Viscous lift force and (b) viscous drag force as a function of the polynomial order k for the compressible, incompressible and vorticity formulations of the DG code with SIPG flux, and the continuous Spectral code Nektar. To assess the influence of the formulation, we consider the steady state case of flow past the square section cylinder at Re = 10 and compare the viscous forces using the three formulations while performing p-refinement. Note that this is a comparison of post- processing techniques and the underlying flow-field is identical for each post-processing formulation. We also compare the results obtained using the DG formulation to the high order Spectral code Nektar. We note that the second order temporal splitting scheme used by Nektar is the same as that used for the present DG implementation but that the space discretisation is different (i.e. continuous vs discontinuous). We show in Fig. 7.a and 7.b the viscous lift and viscous drag components respectively sn ce i Sy ce a a: er ee a | ee a a ie i
    Figure 8: Square section cylinder at Re=100: (a) Strouhal number derived from lift coefficient, (b) mean drag coefficient and (c) RMS lift force coefficient computed with the DG code with SIPG flux, the continuous Spectral code Nektar and Finite Volume code Fluent. Published results'® for Nektar are also included. For the unsteady case with Re = 100, we compare the Strouhal number, St = fb/Ux, where f is the vortex shedding frequency computed from the lift force, b = 1 the length of the cylinder and U,, = 1 the freestream velocity. We note that for this unsteady case, the viscous component is orders of magnitude smaller than the pressure component and hence the formulation used to compute the viscous forces has little influence. Fig. 8.a depicts the results obtained for the variation of St number against the number DOF, for the three solvers together with published results from the Nektar code by Darekar and Sherwin!). We observe that both Nektar and DG give very similar results, providing an accurate solution even for low numbers of DOF. The number of DOF necessary for Fluent to reach comparable accuracy is three times larger than for the two high order methods considered. For completeness, we show the mean drag and RMS lift comparisons using the three codes in Fig. 8.b and 8.c.
    Table 2: Convergence rates for the Poisson equation when performing h-refinement We explore the influence of the penalty parameter, 7, on the solution accuracy for this
    Table 3: Convergence rates for the Helmholtz equation with a = 10 when performing h-refinement The inhomogeneous Helmholtz equation, ic. —Au + au = g, is solved in 2 = [0, 1]?. The wave number \/a can be chosen arbitrarily provided that the forcing term is of the form g(x,y) = (a+ 2n7)cos(mx)cos(ry). The problem is closed using Dirichlet boundary conditions derived from the exact solution u®*“(x,y) = cos(mx)cos(ry). We fix the square of the wave number a = 10, the penalty parameter @ = 1 for all IP formulation and 0 = k(3k +3) for the IPG and SIPG, and as previously, we tabulate the convergence rates for h-refinement using three meshes with 50, 200 and 338 elements in table 3. As before we see that the IIPG method provides better results than predicted by the theory
    Table 4: Results for DG and Nektar for the pressure component of the drag over the square section cylinder at Re=10.
    descriptionView Paperarrow_downwardDownload
    A physics-based shock capturing method for unsteady laminar and turbulent flows
    by Pablo Fernandez

    2018, 56th AIAA Aerospace Sciences Meeting (SciTech 2018), Gaylord Palms, FL, Jan 2018

    We present a shock capturing method for unsteady laminar and turbulent flows. The proposed approach relies on physical principles to increase selected transport coefficients and resolve unstable sharp features, such as shock waves and... more
    descriptionView Paperarrow_downwardDownload
    Comparisons of Compressible and Incompressible Solvers: Flat Plate Boundary Layer and NACA airfoils
    by Esteban Ferrer and 
    1 more
    Gonzalo Rubio

    In proceedings of the 2nd International Work- shop on High Order Methods May 27 - 28, 2013

    This paper presents comparisons of high order Discontinuous Galerkin (DG) solvers using both compressible and incompressible formulations for the solution of the Navier-Stokes equations. The main purpose of this paper is to provide... more
    Figure 5: L? norm of the relative error for the drag coefficient: h/p refinement for a NACA0012 at Re=5000
    Figure 1 shows examples of the grids used for compressible and incompress- ible formulations for a NACAO015. The left triangular mesh is used by the incompressible solver whilst the quadrilateral mesh, on the right, is used by the compressible code. Let us note that the calculations for the NACA0012 are performed in similar grids. Figure 1: NACA0015 airfoil meshes using triangles for the incompressible and quadrilaterals for the compressible solver
    Figure 3: Velocity profiles at a distance of LZ = 5.2 downstream from the leading edge at a Reynolds number of Rez = 520
    Figure 4: L? norm of the relative error for the drag coefficient: flat plate at Rez, = 3600
    Table 1: Summary of test cases detailing Reynolds number, Mach number and Angle of Attack (AOA). We present results for two test cases: ”C1.3 Flow over the NACA0012 airfoil” and ”C1.4 Flat plate Boundary Layer”. In addition to the flow conditions specified by the workshop organisers, we include lower Reynolds numers and various low Mach numbers to study the differences between compressible and incompressible formulations. A summary of the various cases is provided in Table 1.
    Table 2: Viscous drag-coefficients cp, at Rez, = 60 and Re, = 600 for compressible, incompressible and Blasius solution. In addition, results fo the displacement thickness 6/°°“~°”° are summarised
    Table 3: NACA0015 at Re, = 100 and a = 0°. Drag-coefficients ep = ep, + Cp,, including pressure cp, and viscous cp, components, for the compressible and incompressible solvers
    descriptionView Paperarrow_downwardDownload
    A p-Poisson wall distance approach for turbulence modeling
    by Nathan Wukie and 
    1 more
    Paul Orkwis
    Distance fields are an important component of turbulence modeling approaches for computational fluid dynamics. Common approaches for obtaining distance fields include direct search methods as well as methods based on solving a partial... more
    descriptionView Paperarrow_downwardDownload
    Sensitivity analysis to unsteady perturbations of complex flows: a discrete approach
    by Oliver M F Browne and 
    2 more
    Esteban Ferrer
    Gonzalo Rubio

    2014, International Journal for Numerical Methods in Fluids, Vol 76, Issue 12, p1088–1110, 2014

    A discrete framework for computing the global stability and sensitivity analysis to external perturbations for any set of partial differential equations is presented. In particular, a complex-step approximation is used to achieve near... more
    descriptionView Paperarrow_downwardDownload
    Insights on Aliasing Driven Instabilities for Advection Equations with Application to Gauss–Lobatto Discontinuous Galerkin Methods
    by Esteban Ferrer and 
    3 more
    eusebio valero
    juan manzanero
    Gonzalo Rubio
    We analyse instabilities due to aliasing errors when solving one dimensional non-constant advection speed equations and discuss means to alleviate these types of errors when using high order discontinuous Galerkin (DG) schemes. First, we... more
    descriptionView Paperarrow_downwardDownload
    The hybridized Discontinuous Galerkin method for Implicit Large-Eddy Simulation of transitional turbulent flows
    by Pablo Fernandez
    We present a high-order Implicit Large-Eddy Simulation (ILES) approach for transitional aerodynamic flows. The approach encompasses a hybridized Discontinuous Galerkin (DG) method for the discretization of the Navier–Stokes (NS)... more
    descriptionView Paperarrow_downwardDownload
    Stability of projection methods for incompressible flows using high order pressure-velocity pairs of same degree: Continuous and Discontinuous Galerkin formulations
    by Esteban Ferrer and 
    1 more
    Spencer J. Sherwin

    Communications in Computational Physics, Vol 16, Issue 3, p817-840

    This paper presents limits for stability of projection type schemes when using high order pressure-velocity pairs of same degree. Two high order h/p variational methods encompassing continuous and discontinuous Galerkin formulations are... more
    where t represents time, u= (u,v) ' the velocity vector, p the static pressure to density ratio and v the kinematic viscosity. In addition, ug represents an initial condition for the velocity field and Lp defines the Dirichlet boundary data for the velocity. N(u) represents the non-linear contributions expressed, for example, in convective form N(u) =(u-V)u. For a discussion on different non-linear term formulations, the reader is referred to [25] and references therein.
    Here u” denotes u evaluated at time t=nAt, for n €IN. The temporal accuracy is deter- mined by the parameter J, which we fix at two for this work (i.e yo=3/2, a9=2, aj =—1/2, Bo =2 and 6; =—1). Note that in order to solve for the pressure field we assume that the second intermediate velocity field is solenoidal so that V-t=0, and take the divergence of Eq. (2.2) to obtain the pressure Poisson equation
    For both discretisations, the vector of local coefficients a! = (a notes a',...,a@Ne)', where &° de- the local coefficients ii; as defined in equation (2.9), must be related to the global coefficients & = (i1,...,lin ga) Us In the discontinuous framework, since all elements are decou In ord pled we have that a! = 4 (i.e. double valued degrees of freedom at element edges). er to guarantee the continuity of wu, in the C° formulation however, we must en- sure that coefficients along each edge are equal wherever they meet at a common edge Or ver tex. To this end we define an assembly matrix A whereby 4=.A'&! which sums contributions from connected degrees of freedom, ensuring that global coefficients are uniquely defined.
    Let us note that in general, and in particular for the CG formulation, APs and Ae denote the same matrix A if «=0 (see section 2.2.3). However, distinguishing between the matrices arising from solving either the Poisson step or the Helmholtz step, proves advantageous for the analysis and hence this notation will be maintained hereafter.
    Figure 1: Time step refinement study for the unsteady Stokes equations at final time T=0.1, for two meshes and various polynomial orders k. L* relative error norm for continuous and discontinuous formulations (a) CG pressure, (b) CG velocity, (c) DG pressure and (d) DG velocity.
    Figure 2: Time step refinement study for the unsteady Stokes equations at final time T=0.1, 128 triangular element mesh, polynomial order k=4 and three kinematic viscosities v9, vy and v2. L? relative error norm for continuous and discontinuous formulations: (a) CG pressure, (b) CG velocity, (c) DG pressure and (d) DG velocity.
    Figure 3: Eigenvalues for the Poisson matrix (Stokes problem) for continuous and discontinuous Galerkin formulations (a) CG: p-refinement, (b) CG: h-refinement, (c) DG: p-refinement and (d) DG: h-refinement. k denotes the polynomial order and h= (Nei) ~ 1/2 the characteristic mesh size with N, the number of triangular elements in the mesh.
    Figure 4: Time step refinement study for the unsteady Stokes equations, using the DG formulation, at final time T=0.1, for various polynomial orders k. L* relative error norm for (a) pressure and (b) velocity. Gray lines show the original scheme and colored lines the stabilised scheme.
    descriptionView Paperarrow_downwardDownload
    Chapter included in "Recent advances in CFD for Wind and Tidal Offshore Simple models for cross flow turbines
    by Esteban Ferrer

    2019, "Recent advances in CFD for Wind and Tidal Offshore Turbines", Springer Tracts in Mechanical Engineering

    Using a high order discontinuous Galerkin numerical method with sliding meshes, we simulate one, two and three bladed cross-flow turbines to extract statistics of the generated wakes (time averaged velocities and Reynolds stresses).... more
    descriptionView Paperarrow_downwardDownload
    Implicit large-eddy simulation of compressible flows using the Interior Embedded Discontinuous Galerkin method
    by Pablo Fernandez
    We present a high-order implicit large-eddy simulation (ILES) approach for simulating transitional turbulent flows. The approach consists of an Interior Embedded Discontinuous Galerkin (IEDG) method for the discretization of the... more
    descriptionView Paperarrow_downwardDownload
    Discontinuous Galerkin timestepping for nonlinear parabolic problems
    by Mohammad Sabawi

    2018, PhD Thesis, University of Leicester, UK

    We study space–time finite element methods for semilinear parabolic problems in (1 + d)–dimensions for d = 2, 3. The discretisation in time is based on the discontinuous Galerkin timestepping method with implicit treatment of the linear... more
    descriptionView Paperarrow_downwardDownload
    Stability of the high-order finite elements for acoustic or elastic wave propagation with high-order time stepping
    by Jonas De Basabe
    We investigate the stability of some high-order finite element methods, namely the spectral element method and the interior-penalty discontinuous Galerkin method (IP-DGM), for acoustic or elastic wave propagation that have become... more
    The second part of this method is to obtain a Taylor expansion for the time stepping. Evaluating the Taylor expansion of x at t + At and t — At yields Theorem 1. The 24th order time derivative of x is given by The application of the LWM to eq. (42) has been described in Cohen (2002) and Dablain (1986). It is interesting to note that this method usually bears other names when it is applied to second order systems, for example, in Cohen (2002) it is called the modified equation approach. Nevertheless, due to the important similarities with the original formulation, it is suitable to regard this as a LWM. The first part of this method is to obtain an expression that allows the substitution of the higher-order time derivatives by matrix operation, which is given by the following theorem.
    Figure 1. Numerical anisotropy introduced by the grid dispersion using SEM of degrees 2-4, the second order LWM (leap-frog finite differences), r = 2 and 6 = 0.2 (five gridpoints per wavelength). The dispersion has been magnified for visualization purposes using the following number of wavelengths: (a) 100, (b) 500 and (c) 1000.
    Figure 2. Numerical anisotropy introduced by the grid dispersion using SIPG of degrees 2 to 4, the 2nd order LWM (leap-frog finite differences), r = 2 and 6 = 0.2. The dispersion has been magnified for visualization purposes using the following number of wavelengths: (a) 300, (b) 3000 and (c) 10000.
    Figure 3. Numerical anisotropy introduced by the grid dispersion using SEM of degrees 2 to 4 and LWM of orders | to 3.
    Figure 4. Numerical anisotropy introduced by the grid dispersion using SIPG of degrees 2 to 4 and LWM of orders | to 3.
    Figure 5. Synthetic seismograms for Lamb’s problem using the fourth- degree SEM and the 2nd order FDM.
    Figure 6. Synthetic seismograms for Lamb’s problem using the fourth- degree SEM and the fourth-order LWM.
    Figure 7. Synthetic seismograms for Lamb’s problem using the fourth- degree IP-DGM and the 2nd order FDM.
    Figure 8. Synthetic seismograms for Lamb’s problem using the degree IP- DGM and the fourth-order LWM.
    Table 1. Upper bounds for the stability parameter in the acoustic case. Notes: The constants for SIPG, IIPG and NIPG are computed using the GLL basis functions. The last two columns correspond to SIPG using the Gauss and Legendre basis functions.
    Note: The constants for SIPG, IIPG and NIPG are computed using the GLL basis functions. Table 2. Upper bounds for the modified stability parameter q/’ in the acous- tic case.
    Note: The constants for SIPG, IPG and NIPG are computed using the GLL basis functions. Table 3. Upper bounds for the stability parameter in the elastic case using r=141,.
    Note: The constants for SIPG, IPG and NIPG are computed using the GLL basis functions. Table 4. Upper bounds for the modified stability parameter q’ in the elastic case using r = 1.41.
    Table 6. Comparison of the RMS error of the seismograms for Lamb’s problem (Figs 5-8) using a time step 90, 50 anc 25 per cent of the CFL stability condition reported in Table 3 and fourth-degree SEM and IP-DGM.
    and S = {T, B, L, R} represent the four surrounding elements from the top, bottom, left and right to the reference element FE.
    descriptionView Paperarrow_downwardDownload
    Méthode des éléments finis Galerkin discontinue pour l'élastodynamique haute fréquence
    by Eric Savin

    2010, Sofiane Aoutou - MSc Thesis, Université Henri-Poincaré Nancy I

    Spécialité : Calcul scientifique STAGE à L'Office national d'études et recherches aérospatiales Méthode des éléments finis Galerkin discontinue pour l'élastodynamique haute fréquence Du 1 er avril 2010 au 30 septembre 2010 AVANT-PROPOS... more
    descriptionView Paperarrow_downwardDownload
    A Lecture on Simulating behavior of a mass-spring-damper system in Matlab through analytical and numerical solution
    by Dr. Redmond R . Shamshiri
    Simulating behavior of a mass-spring-damper system in Matlab through analytical and numerical solution
    descriptionView Paperarrow_downwardDownload
    Analysis of seabed instability using element free Galerkin method
    by Mohamed Rehan Karim

    2007, Ocean Engineering

    Wave-induced seabed instability, either momentary liquefaction or shear failure, is an important topic in ocean and coastal engineering. Many factors, such as seabed properties and wave parameters, affect the seabed instability. A... more
    descriptionView Paperarrow_downwardDownload
    A Chimera-based, zonal discontinuous Galerkin method
    by Nathan Wukie and 
    1 more
    Paul Orkwis
    In order to achieve increased computational efficiency in a design environment, a Chimera based, zonal discontinuous Galerkin(DG) approach was developed incorporating a two-fidelity model. The higher-fidelity models solve the full... more
    descriptionView Paperarrow_downwardDownload
    A spectral hybridizable discontinuous Galerkin method for elastic-acoustic wave propagation
    by laurent guillot and 
    1 more
    Sébastien Terrana
    SUMMARY We introduce a time-domain, high-order in space, hybridizable discontinuous Galerkin spectral element method (HDG-SEM) for wave equations in coupled elastic-acoustic media. The method is based on a first-order hyperbolic... more
    Figure 1. (a) Elastic-elastic domain decomposition : on the interface Tg, the field © is single-valued while on is double-valued. (b) Acoustic-acoustic domain decomposition : on Typ the field 6, is single- valued while 6 is double-valued. (c) Acoustic-elastic domain decomposition : on Tyg the field 6, is single-valued while the hybrid pressure p and the hybrid traction on are defined on the acoustic and elastic sides respectively. Figure 1. (a) Elastic-elastic domain decomposition : on the interface I's;, the field 6 is single-valued
    Figure 2. Riemann problem in the vicinity of an interface point xp € T°
    Figure 3. Left : Riemann problem associated to discontinuous states of q at the interface. Right : This leads to hybridized versions of the Riemann solvers previously presented by Wilco
    Figure 4. Negative characteristic lines used to build (on) part of the resulting vectorial equality, one get
    Figure 5. Positive characteristic curves used to build (o7)3
    Figure 6. Negative characteristic curves used to build «~ €, for acoustic-acoustic interface be similarly determined as
    Figure 7. Characteristic lines for an acoustic-elastic interface. Here 7” is the acoustic impedance, and is the scalar counterpart of the elastic 7~ matrix
    Figure 8. Lamb’s Test configuration and velocity norm fields at times t = 0.75 sec (top) and t = 2 sec
    Figure 9. Lamb’s problem: errors and convergence orders observed. Left: L?-errors for the numerice
    Figure 10. Elastic-acoustic test configuration. The magnitude of the velocity fields are shown a‘
    Figure 11. Elastic-acoustic test case : the L?-norm of the velocity error (left) and the estimated orders of convergence (right) are shown for different order of element polynomial approximation N. »ML absorption does not affect the convergence results
    Figure 12. On the left, configuration of the two-layer computational domain, with the localisations of
    Figure 13. Top : time response of the horizontal and vertical components of the displacement at the horizontal line of receivers located within the top layer as obtained with the HDG-SEM method. The direct P-wave (a) can be clearly distinguished, as well as a strong Rayleigh-to-body-wave (d) generated by the free surface curvature. This wave travels at the S-wave speed and can not always be clearly distinguished from the main S-wave in this figure. Bottom : horizontal and vertical velocities recorded at receiver 50 for the HDG-SEM method, together with the error residual when compared with the CG-SEM solution.
    Figure 14. Upper left : test confiuration for the CG-SEM and HDG-SEM coupling. Upper right : snapshot of the velocity norm at time t = 1.5 sec. Lower left and right : velocity components recorded at the receiver located in the HDG domain. The amplified difference between the numerical solution and the CG-SEM reference solution is shown in blue. The difference remains small even after several wave transmissions across the coupling interface.
    Figure 15. Left : Numerical domain for the seismic-infrasonic simulation. Right : vertical evolution
    The complexity of the generated wave field can clearly be observed on the velocity snap-
    Figure 17. Top : Schematic representation of the Antilles section studied. Below : three successive 8 CONCLUSION We have presented a HDG-SEM method for solving elastic-acoustic wave propagation in
    where Ay, = nzAz + nyAy +n,A, is simply expressed in terms of the Lamé parameters as
    the conservativity condition (25) with the weakly imposed Neumann condition on Q7 NT Moreover, results from section 4 allow to express on and # as
    stage. The LSERK4 method is implemented as algorithm 1. The coefficients a;, bj, c; are given in Carpenter & Kennedy (1994). Note that ¢”*@ mean
    and elastic-acoustic problems. The symbol (*) means that post-processing has been performed. The authors warn that none of the implementations used here have been seriously opti- DG and HDG decrease with the polynomial order.
    descriptionView Paperarrow_downwardDownload
    Discontinuous Galerkin Finite Element Approximation of the Cahn-Hilliard Equation with Convection
    by amal gh

    2009, Siam Journal on Numerical Analysis

    The paper is concerned with the construction and convergence analysis of a discontinuous Galerkin finite element method for the Cahn-Hilliard equation with convection. Using discontinuous piecewise polynomials of degree p ≥ 1 and backward... more
    descriptionView Paperarrow_downwardDownload
    High-order nodal discontinuous Galerkin methods for the Maxwell eigenvalue problem: One contribution of 13 to a Theme 'Short-wave scattering
    by Jan S Hesthaven

    2004, Philosophical Transactions of the Royal Society of London a Mathematical Physical and Engineering Sciences

    The Maxwell eigenvalue problem is known to pose difficulties for standard numerical methods, predominantly due to its large null space. As an alternative to the widespread use of Galerkin finite-element methods based on curl-conforming... more
    descriptionView Paperarrow_downwardDownload
    A SIMPLE based discontinuous Galerkin solver for steady incompressible flows
    by Martin Oberlack

    2013, Journal of Computational Physics

    In this paper we present how the well-known SIMPLE algorithm can be extended to solve the steady incompressible Navier-Stokes equations discretized by the discontinuous Galerkin method. The convective part is discretized by the local... more
    We aim to solve the steady incompressible Navier-Stokes Eqs. (1a)-(1e) for the unknown DG coefficients Te and p!" of the approximated velocity uj; € V, and the approximated pressure p, € Vy, with k’ = k for an equal-order formulation or k’ = k—1 for a mixed-order formulation. To represent the Navier-Stokes equations in V,, we define the discrete operators In (10a), the non-linear term of the momentum equation is written as Ac(uj) - uj. Within the SIMPLE algorithm, this term will be linearized, cf. Section 3. The definitions for the numerical fluxes F°, F?, F? and F” in (10a)-(10d) are given in the follow- ing Sections 2.3-2.5. The vectors Dc,, bp,, bp,, bg, are the affine-linear offsets of the operators following from non-zero bound- ary conditions and by includes all source terms. Setting 2.2. Discrete system of equations
    Fig. 1. H-convergence for the Poiseuille flow using equal- and mixed-order formulations with best linear fits in a least square sense and its slopes Performance of the SIMPLE algorithm for the different test cases: optimal values for the relaxation factors «, and a), degrees of freedom (DOF) for velocity an pressure, number of SIMPLE iterations and computational time. coarsest grid with 4 x 20 cells. As boundary conditions we apply the analytical solution u;(0,x2) = 1 — x}, u2(0,x2) = 0 at the inlet, the no-slip condition at the walls and du, /0x1|, 19 = 0, 0U2/OX1|,. 19 = 0, p(10,x2) = O at the outlet. aU “ Wer om IR = RS SIRT: inlet, the no-slip condition at the walls and du /0X1|y,-19 = 0, OU2/OX1|y,-10 = 0, p(10, x2) = O at the outlet. Simulations are performed on four different grids for equal-order k = 1,k’ = 1 and mixed-order formulations k = 1,k’ = 0. The L?-norm of the error of the velocity u; with respect to the analytical solution versus the grid size is shown in Fig. 1, where the parameter for the grid size is normalized with respect to the coarsest grid, i.e. Ax = Ax;/Axo. For both formulations, the convergence rates for the velocity u, are in very good agreement with the theoretical one of k + 1. The results for the equal- order formulation are slightly more accurate than those for the mixed-order formulation. Note that DG orders of k > 2 and k’ > 1 are already able to represent the exact solution, even with only one cell for the whole domain.
    Fig. 2. Profiles of velocity u, for k = 1 (top left), k = 2 (top right) and k = 3 (bottom) for the channel flow with constant transpiration on a grid with 4 x 20 cells - circles: simulation, line: analytical solution. The analytical solution for the streamwise velocity profile and the numerical results on a grid with 4 x 20 cells for the DG orders k = 1,k = 2 and k = 3 are shown in Fig. 2. It can be seen how the difference between the analytical solution and the simulation is becoming smaller for higher DG orders. In Fig. 3 the p-convergence on the coarsest grid with 4x 20 cells and the h-convergence for the velocity u; are presented. The errors are calculated in the L?-norm. For the p-convergence the polynomial degrees k = 1,...,8 are used for the velocity. According to the mixed-order formula- tion the polynomial degree k’ for the pressure is always one order lower. As expected, for the p-convergence an expo- nential rate of convergence can clearly be seen. The test of the h-convergence is performed on four different grids with polynomial orders k=1,...,5 and k’=0,...,4. The results show the optimal rate of convergence of k+1 for the velocity.
    Fig. 3. P-convergence (left) on a grid with 4 x 20 cells and h-convergence (right) for velocity u, for the channel flow with constant transpiration. For the h- convergence the best linear fits in a least square sense and the corresponding slopes of the L” errors are also plotted. 4.4, Kovasznay flow The Kovasznay flow [13], which may be considered as the flow behind a two-dimensional grid, has the analytical solution
    Fig. 4. H-convergence for velocity (left) and pressure (right) for the Kovasznay flow. The best linear fits in a least square sense and the corresponding slope: of the L” errors are also plotted.
    Fig. 5. Streamlines (left) and contour plot of the pressure (right) on a grid with 24 x 24 cells with polynomial orders k = 5, k’ = 4 for the flow into a corner test case. The backward-facing step flow is widely used as a benchmark test for numerical simulations. We set up the calculation according to the experiment by Armaly et al. [14]. The dimensionless geometry and a part of the non-uniform Cartesian grid close to the step is depicted in Fig. 7. The length of the channel is chosen to make sure that the flow is fully developed at the outlet, i.e. Ou; /Ox; = 0 and du /0x; = 0. The geometry is made dimensionless with twice the height of the channel at the inlet, L = 2h, and two-thirds of the maximum of the streamwise velocity u; at the same position, U = 2/3Umax. Then the
    Fig. 6. H-convergence for velocity (left) and pressure (right) for the flow into a corner test case. The best linear fits in a least square sense and the corresponding slopes of the L” errors are also plotted. eynolds number is Re = 4Umax/t/(3v), where v is the kinematic viscosity. At the walls the no-slip condition is applied and 1e boundary conditions at the inlet (x; = —2) and outlet (x; = 26) are
    Fig. 7. Geometry (top) and close-up of the grid (bottom) for the backward-facing step flow. The entire grid consists of 3328 cells and the polynomial orders are k = 5 for the velocity and k’ = 4 for the pressure. For the Reynolds number we take Re = 300. Following [14], for this Reynolds number the flow is still laminar, two-dimensional and there is only one recirculation zone. In Fig. 8 profiles of the velocity u; are plotted at different positions in the streamwise direction. Like in the experiment, we also find only one zone of recirculation in our calculation. Our point of reattachment is at (Xr, Ye) = (3.1, -0.47), which agrees very well with the values reported in [14]. Figs. 9 and 10 show a contour plot of the pressure and the streamlines in the region close to the step, respectively. In the plot of the pressure the singularity at the corner of the step can be clearly observed.
    Fig. 8. Profiles of the streamwise velocity at different locations for the backward-facing step flow.
    Fig. 9. Contour plot of the pressure close to the step for the backward-facing step flow.
    Fig. 10. Streamlines close to the step for the backward-facing step flow.
    Number of SIMPLE iterations as a function of the relaxation factors «, and a» for the Poiseuille flow using a grid with 4 x 20 cells and tolerances for ||pj\|;2,) a ||ujiét — upill;2() Of 1.0e-10. The optimal value is bold-faced.
    Number of SIMPLE iterations as a function of the relaxation factors «, and «, for the channel flow with constant transpiration using a grid with 4 x 20 cells anc tolerances for ||pj,||,2¢9) and jue? — we \|2;@) Of 1.0e-10. The optimal value is bold-faced. hi hi
    Number of SIMPLE iterations as a function of the relaxation factors «, and , for the Kovasznay flow using a grid with 8 x 8 cells and tolerances for ||), |\,2(, an¢ \|up;'! — Upilli2¢@) Of 1.0e-10. The optimal value is bold-faced. hi
    Number of SIMPLE iterations as a function of the relaxation factors «, and , for the flow into a corner using a grid with 6 x 6 cells and tolerances for ||pj,||,2 (@ and |jujt! — upill2(@) Of 1.0e-5. The optimal value is bold-faced.
    Number of SIMPLE iterations as a function of the relaxation factors «, and «, for the backward-facing step flow using a grid with 832 cells and tolerances for lPhlliz@) and uett ue \l2;@) Of 1.0e-6. The optimal value is bold-faced. hi hi
    Table 6
    descriptionView Paperarrow_downwardDownload
    Solución de la ecuación de Rayleigh-Plesset por medio del método del elemento finito
    by Revista Ingeniería y Ciencia and 
    1 more
    G.A. Ramírez Ramírez

    2013

    "En este trabajo se plantean soluciones numéricas a la ecuación de Rayleigh-Plesset que describe la evolución de las burbujas en la cavitación. Para ello, se considera el MEFG (Método del Elemento Finito de Galerkin); tal simulación se... more
    descriptionView Paperarrow_downwardDownload
    C 0 Discontinuous Galerkin Methods for a Kirchhoff Plate Contact Problem
    by Fei Wang
    Numerous C 0 discontinuous Galerkin (DG) schemes for the Kirchhoff plate bending problem are extended to solve a plate frictional contact problem, which is a fourth-order elliptic variational inequality of the second kind. This... more
    descriptionView Paperarrow_downwardDownload
    Unstructured, curved elements for the two-dimensional high order discontinuous control-volume/finite-element method
    by Goran Stipcich

    2015, International Journal for Numerical Methods in Engineering

    Quadrilateral and triangular elements with curved edges are developed in the framework of spectral, discontinuous, hybrid control-volume/finite-element method for elliptic problems. In order to accommodate hybrid meshes, encompassing both... more
    descriptionView Paperarrow_downwardDownload
    Dynamique transitoire de treillis de poutres tridimensionnels soumis à des chargements impulsionnels
    by Eric Savin
    Dans ce travail de recherche, la dynamique transitoire de treillis de poutres de Timoshenko tridimensionnels soumis à des chocs mécaniques ou acoustiques est étudiée grâce à un modèle de transport de l’énergie vibratoire. Celui-ci permet... more
    descriptionView Paperarrow_downwardDownload
    Discontinuous finite elements with high degree polynomial interpolation for transport equations
    by Eric Savin

    2013, Daniel del Pozo Galan - MSc Thesis, Ecole Centrale Lille & Universidad Politecnica Madrid

    descriptionView Paperarrow_downwardDownload
    An Efficient ELLAM Implementation for Modeling Solute Transport in Fractured Porous Media
    by Husam Baalousha and 
    2 more
    Fanilo Ramasomanana
    Nicolas Barth
    The goal of this study is to introduce an adaptation of the Eulerian-Lagrangian localized adjoint method (ELLAM) for the simulation of mass transport in fractured porous media, and to evaluate the performance of ELLAM in such a case. The... more
    descriptionView Paperarrow_downwardDownload
    A reconstructed discontinuous Galerkin method for the compressible Navier–Stokes equations on arbitrary grids
    by Nam Dinh

    2010, Journal of Computational Physics

    A reconstructed discontinuous Galerkin (RDG) method based on a Hierarchical WENO reconstruction, termed HWENO(P 1 P 2 ) in this work, designed not only to enhance the accuracy of discontinuous Galerkin method but also to ensure the... more
    descriptionView Paperarrow_downwardDownload
    Reproducing Kernel Element Method for Galerkin Solution of Elastostatic Problems
    by Revista Ingeniería y Ciencia

    2012

    "The Reproducing Kernel Element Method (RKEM) is a relatively new techniquedeveloped to have two distinguished features: arbitrary high ordersmoothness and arbitrary interpolation order of the shape functions. This paper provides a... more
    Figure 14: Problem statement. Reproducing Kernel Element Method for Galerking Solution of Elastostatic Problems
    Figure 17: Solution using the mesh showed in Fig [15() vertical displacement.
    where t; correspond to the value of the function to interpolate and evaluated at the node 7. We can manipulate terms so that we can get the following representation of the same equation.
    Figure 3: Window function and its derivative for w(x) = (1 — x)’ Reproducing Kernel Element Method for Galerking Solution of Elastostatic Problems
    2.3.1 Radial Window Function In two dimensions a node’s domain of influence covers an area in the domain. The choice of the shape of this domain is arbitrary. However, circular domain or square domains have been used most frequently. In this work we have used the circular domains for all the computation. In RKEM the radius of the circle can not be arbitrary, it need to be a function of the mesh [10]. The scheme for the circular domain is shown in Fig. The window function definition in 2D used in this work will be:
    Figure 5: RKEM mesh and and global shape function for node 4. The computation of the stiffness and load vectors requires integration of the shape functions and products of derivatives of shape functions. The RKEM functions are piecewise rational functions that are able to reproduce polyno- mials. As can be seen in the plots of the shape function in Fig. [5]the functions are globally continuous and smooth. In Fig. [6] we can see typical entries to integrate in the weak form. Note that due to the strong oscillation this kind of functions are difficult to integrate exactly. Even though the RKEM shape functions are not polynomials, Gauss quadrature is used anyway. We used the work presented in to generate Gauss points for a triangular domain. Currently, 64 quadrature points per element are used to integrate the T9P2I1 element. Still, the problem of finding an optimal quadrature rule to integrate exactly the weak form is an open research area.
    Figure 6: Typical elements to integrate in the stiffness matrix. We have used the T9P2I1 element. 2.5 Discrete Equations in 2D
    Reproducing Kernel Element Method for Galerking Solution of Elastostatic Problems The displacement field calculated with RKEM is nearly exact and conti- nuous. Note that we can generate a globally continuous function with just twe nodes. It should be noted that these results were plotted using 200 sampling points along the bar. In Fig. [9] we can observed the solution in the derivative. Note that, unlike finite element, our solution in derivative is continuous. Re- member that for the case of linear finite element the stresses are approximatec by a constant values along the element, thus we have jumps between elements The L2P1I0 element used in this example is not that important for practica application, but was chosen because it easy to show how the RKEM methoc works. In Section [2.3] we use a higher order element in 2D.
    Figure 10: Domain for plane stress elasticity problem.
    not using any post process to deal with the stress plot.
    Figure 12: Solution for the 4 by 1 series.
    descriptionView Paperarrow_downwardDownload
    Basis functions for solving the transport equation
    by Eric Savin

    2011, Christina Yassouridis - MSc Thesis, Université Pierre-et-Marie-Curie

    descriptionView Paperarrow_downwardDownload
    FAST TRACK PAPER: The interior penalty discontinuous Galerkin method for elastic wave propagation: grid dispersion
    by Jonas De Basabe

    2008, Geophysical Journal International

    Recently, there has been an increased interest in applying the discontinuous Galerkin method (DGM) to wave propagation. In this work, we investigate the applicability of the interior penalty DGM to elastic wave propagation by analysing... more
    descriptionView Paperarrow_downwardDownload
    The interior penalty discontinuous Galerkin method for elastic wave propagation: grid dispersion
    by Jonas De Basabe
    Recently, there has been an increased interest in applying the discontinuous Galerkin method (DGM) to wave propagation. In this work, we investigate the applicability of the interior penalty DGM to elastic wave propagation by analysing... more
    descriptionView Paperarrow_downwardDownload
    A hybrid DGTD-TDIE method for solving complex electromagnetic problems
    by Siping Gao
    descriptionView Paper
    Pixel-exact rendering of spacetime finite element solutions
    by Robert Haber

    2004, Visualization, 2004. IEEE

    : Shock waves propagating through a partial 2-D cross-section of a solid rocket booster.
    descriptionView Paperarrow_downwardDownload
    Download research papers for free!
    580 California St., Suite 400
    San Francisco, CA, 94104