Academia.eduAcademia.edu

Outline

Title
Abstract
Key Takeaways
Figures
Results
Discussion and Conclusions
Materials and Methods
References
All Topics
Physics
Statistical and Nonlinear Physics

Universal scaling of active nematic turbulence

Profile image of Jaume CasademuntJaume Casademunt

2020, Nature Physics

https://doi.org/10.1038/S41567-020-0854-4
visibility

…

description

13 pages

link

1 file

Abstract
sparkles

AI

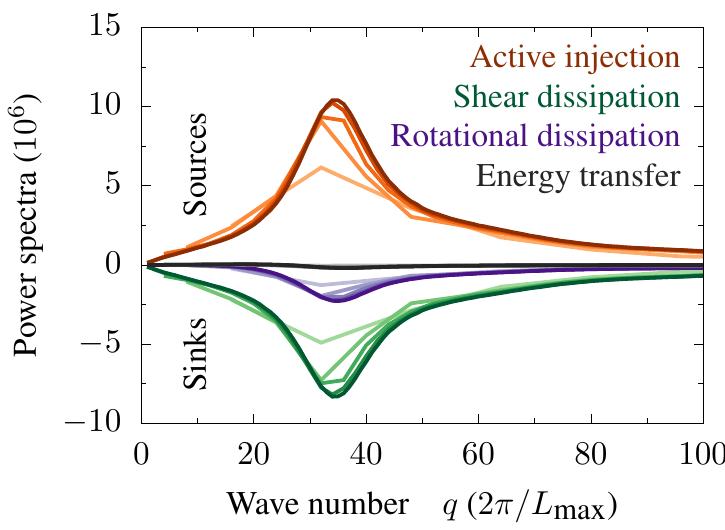
Active nematic fluids exhibit turbulent-like behavior at low Reynolds numbers, yet their universal scaling properties remain uncertain. A minimal defect-free model is proposed to investigate these fluids, revealing a universal scaling of the kinetic energy spectrum of E(q) ∼ q^{d-3} (d > 1) at long wavelengths. Energy injection peaks at a characteristic length scale, and while energy cascades are precluded due to immediate dissipation, long-range velocity correlations arise from non-local Stokes flow, establishing a distinct universality class of turbulence.

Key takeaways
sparkles

AI

  1. Active nematic fluids exhibit turbulent flows with universal scaling properties at large length scales.
  2. Energy injection occurs at all scales, peaking at a characteristic wavelength determined by nonlinear dynamics.
  3. The scaling regime is established by long-range hydrodynamic interactions, not by energy cascades.
  4. Kinetic energy and enstrophy spectra scale as E(q) ∼ q^(-3) and E(q) ∼ q^(-1), respectively.
  5. The study introduces a minimal model for active nematic turbulence, revealing unique properties compared to inertial turbulence.
Figures (7)
Figure 1. Stationary patterns upon the spontaneous flow instability. (A) Growth rate Eq. (8) of perturbations transverse to the director (¢ = 7/2) for a contractile system (S = —1) with R = 1. The crit- ical wavelength ~ @, decreases with the activity number A. Points indicate numerical results (Methods), with discrete wave numbers for a system of size L. (B) Stripe pattern and the corresponding spon- taneous shear flow for A = 200. (C) Stable vortex pattern at higher activity number A = 500. Small bars indicate the director (top). Lines with arrows indicate streamlines (bottom). Vortex patterns).
Figure 1. Stationary patterns upon the spontaneous flow instability. (A) Growth rate Eq. (8) of perturbations transverse to the director (¢ = 7/2) for a contractile system (S = —1) with R = 1. The crit- ical wavelength ~ @, decreases with the activity number A. Points indicate numerical results (Methods), with discrete wave numbers for a system of size L. (B) Stripe pattern and the corresponding spon- taneous shear flow for A = 200. (C) Stable vortex pattern at higher activity number A = 500. Small bars indicate the director (top). Lines with arrows indicate streamlines (bottom). Vortex patterns).
Figure 2. Disordered pattern of director domains with a characteristic wavelength. (A) Snapshot of the angle field for a system size of 2048 x 2048 grid points at activity number Amax = 3.2 - 10°. (B) The spectrum of the Frank elastic energy Eq. (4) (Eq. (S29), units of K/Lmax) is peaked at an intrinsic wavelength \; ~ £- independent of system size. Here, £. is held fixed (Cc = Lmax/WAmax © Dmax /566), such that the activity number A = L* /£2 increases with system size L = n&. The wave number is rescaled by the largest system size Lomax, Such that the axis shows the mode number in the largest system (n = 2048).
Figure 2. Disordered pattern of director domains with a characteristic wavelength. (A) Snapshot of the angle field for a system size of 2048 x 2048 grid points at activity number Amax = 3.2 - 10°. (B) The spectrum of the Frank elastic energy Eq. (4) (Eq. (S29), units of K/Lmax) is peaked at an intrinsic wavelength \; ~ £- independent of system size. Here, £. is held fixed (Cc = Lmax/WAmax © Dmax /566), such that the activity number A = L* /£2 increases with system size L = n&. The wave number is rescaled by the largest system size Lomax, Such that the axis shows the mode number in the largest system (n = 2048).
Figure 3. Spectra of the four contributions to the energy balance Eq. (9) (Eq. (S32)). These results are for the largest system size with 2048 x 2048 grid points at activity number A = 3.2 - 10°. Fig. S2 shows results for smaller systems. The active energy injection is en- tirely balanced by dissipation at every scale; no energy is transferred between scales. The energy injection rate is maximal at the selected wavelength \,;.
Figure 3. Spectra of the four contributions to the energy balance Eq. (9) (Eq. (S32)). These results are for the largest system size with 2048 x 2048 grid points at activity number A = 3.2 - 10°. Fig. S2 shows results for smaller systems. The active energy injection is en- tirely balanced by dissipation at every scale; no energy is transferred between scales. The energy injection rate is maximal at the selected wavelength \,;.
Figure 4. Universal scaling of the flow spectra at large scales. (A) Snapshot of the stream function field for a system size of 2048 x 2048 grid points at activity number Amax = 3.2 - 10°. The small background ripples correspond to coherent vortices of typical size given by the scale of maximal energy injection 4;. However, large-scale correlated flow patches also form due to the non-local character of viscous flow. Lines with arrows indicate a few streamlines that highlight these large-scale circulations. (B-C) The spectra of kinetic energy and enstrophy Eq. (10) (Eqs. (S35) and (S38)) exhibit a peak at the maximal injection scale A;. At smaller and, importantly, also at larger scales, the spectra feature distinctive universal scaling regimes. As in Fig. 2B, @. is held fixed (€¢ = Dmax/VAmax © Dmax/566), such that the activity number A = L*/€2 increases with system size L = nA. The wave number is rescaled by the largest system size Lmax, such that the axis shows the mode number in the largest system (n = 2048).
Figure 4. Universal scaling of the flow spectra at large scales. (A) Snapshot of the stream function field for a system size of 2048 x 2048 grid points at activity number Amax = 3.2 - 10°. The small background ripples correspond to coherent vortices of typical size given by the scale of maximal energy injection 4;. However, large-scale correlated flow patches also form due to the non-local character of viscous flow. Lines with arrows indicate a few streamlines that highlight these large-scale circulations. (B-C) The spectra of kinetic energy and enstrophy Eq. (10) (Eqs. (S35) and (S38)) exhibit a peak at the maximal injection scale A;. At smaller and, importantly, also at larger scales, the spectra feature distinctive universal scaling regimes. As in Fig. 2B, @. is held fixed (€¢ = Dmax/VAmax © Dmax/566), such that the activity number A = L*/€2 increases with system size L = nA. The wave number is rescaled by the largest system size Lmax, such that the axis shows the mode number in the largest system (n = 2048).
Figure S1. Probability distribution of the active power J for different system sizes L = nA. Here, ¢. is held fixed (C2 = Dmax/VAmax © Imax /566), such that the activity number A = L? / 2 increases with system size L. Negative and positive values of I respectively cor- respond to active energy absorption and injection into the system. Therefore, on average, active stresses inject energy to drive the flows.
Figure S1. Probability distribution of the active power J for different system sizes L = nA. Here, ¢. is held fixed (C2 = Dmax/VAmax © Imax /566), such that the activity number A = L? / 2 increases with system size L. Negative and positive values of I respectively cor- respond to active energy absorption and injection into the system. Therefore, on average, active stresses inject energy to drive the flows.
Figure $2. Spectra of the four contributions to the energy balance Eq. (9) (Eq. (S32)) for different system sizes L = nA. Here, @ is held fixed (€. = Lmax/WVAmax © Dmax/566), such that the activity number A = L?/€? increases with system size L. The wave number is rescaled by the largest system size max, such that the axis shows the mode number in the largest system (n = 2048).
Figure $2. Spectra of the four contributions to the energy balance Eq. (9) (Eq. (S32)) for different system sizes L = nA. Here, @ is held fixed (€. = Lmax/WVAmax © Dmax/566), such that the activity number A = L?/€? increases with system size L. The wave number is rescaled by the largest system size max, such that the axis shows the mode number in the largest system (n = 2048).
Figure S3. Power spectrum of the vorticity source Eq. (S43) for different system sizes L = nA. Here, @. is held fixed (@. = Lmax/V Amax © LDmax/566), such that the activity number A = L? /€2 increases with system size L. The wave number is rescaled by the largest system size Lmax, such that the axis shows the mode number in the largest system (n = 2048).
Figure S3. Power spectrum of the vorticity source Eq. (S43) for different system sizes L = nA. Here, @. is held fixed (@. = Lmax/V Amax © LDmax/566), such that the activity number A = L? /€2 increases with system size L. The wave number is rescaled by the largest system size Lmax, such that the axis shows the mode number in the largest system (n = 2048).

Related papers

Universality in turbulence: An exactly soluble model
Antti Kupiainen

1995

The present note contains the text of lectures discussing the problem of universality in fully developed turbulence. After a brief description of Kilmogorov's 1941 scaling theory of turbulence and a comparison between the statistical approach to turbulence and field theory, we discuss a simple model of turbulent advection which is exactly soluble but whose exact solution is still difficult to analyze. The model exhibits a restricted universality. Its correlation functions contain terms with universal but anomalous scaling but with non-universal amplitudes typically diverging with the growing size of the system. Strict universality applies only after such terms have been removed leaving renormalized correlators with normal scaling. We expect that the necessity of such an infrared renormalization is a characteristic feature of universality in turbulence.

View PDFchevron_right
UNIVERSALITY in TURBULENCE: an EXACTLY SOLUBLE MODEL1
Antti Kupiainen

Nasa Sti Recon Technical Report N, 1995

The present note contains the text of lectures discussing the problem of universality in fully developed turbulence. After a brief description of Kolmogorov's 1941 scaling theory of turbulence and a comparison between the statistical approach to turbulence and field theory, we discuss a simple model of turbulent advection which is exactly soluble but whose exact solution is still difficult to analyze. The model exhibits a restricted universality. Its correlation functions contain terms with universal but anomalous scaling but with non-universal amplitudes typically diverging with the growing size of the system. Strict universality applies only after such terms have been removed leaving renormalized correlators with normal scaling. We expect that the necessity of such an infrared renormalization is a characteristic feature of universality in turbulence.

View PDFchevron_right
Universality of anisotropic turbulence
Luca Biferale

Physica A: Statistical Mechanics and its Applications, 2004

We review some ideas about the physics of small-scale turbulent statistics, focusing on the scaling behavior of anisotropic uctuations. We present results from direct numerical simulations of three-dimensional homogeneous, anisotropically forced, turbulent systems: the Rayleigh-BÃ enard system, the random-Kolmogorov-ow, and a third ow with constant anisotropic energy spectrum at low wave numbers. A comparison of the anisotropic scaling properties displays good similarity among these very di erent ows. Our ÿndings support the conclusion that scaling exponents of anisotropic uctuations are universal, i.e., independent of the forcing mechanism sustaining turbulence.

View PDFchevron_right
Scaling exponents in weakly anisotropic turbulence from the Navier–Stokes equation
Detlef Lohse

Journal of Fluid Mechanics, 2001

The second-order velocity structure tensor of weakly anisotropic strong turbulence is decomposed into its SO(3) invariant amplitudes d j (r). Their scaling is derived within a scaling approximation of a variable-scale mean-field theory of the Navier-Stokes equation. In the isotropic sector j = 0 Kolmogorov scaling d 0 (r) ∝ r 2/3 is recovered. The scaling of the higher j amplitudes (j even) depends on the type of the external forcing that maintains the turbulent flow. We consider two options: (i) for an analytic forcing and for decreasing energy input into the sectors with increasing j, the scaling of the higher sectors j > 0 can become as steep as d j (r) ∝ r j+2/3 ; (ii) for a non-analytic forcing we obtain d j (r) ∝ r 4/3 for all non-zero and even j.

View PDFchevron_right
Anomalous scaling in fluid mechanics: The case of the passive scalar
Victor L'Vov

Physical Review E, 1994

A mechanism for anomalous scaling in turbulent advection of passive scalars is identified as being similar to a recently discovered mechanism in Navier-Stokes dynamics [V. V. Lebedev and V. S. L'vov, JETP Lett. 59, 577 (1994)l. This mechanism is demonstrated in the context of a passive scalar field that is driven by a rapidly varying velocity field. The mechanism is not perturbative, and its demonstration within renormalized perturbation theory calls for a resummation of infinite sets of diagrams. For the example studied here we make use of a small parameter, the ratio of the typical time scales of the passive scalar vs that of the velocity field, to classify the diagrams of renormalized perturbation theory such that the relevant ones can be resummed exactly. The main observation here, as in the Navier-Stokes counterpart, is that the dissipative terms lead to logarithmic divergences in the diagrammatic expansion, and these are resummed to an anomalous exponent. The anomalous exponent can be measured directly in the scaling behavior of the dissipation two-point correlation function, and it also affects the scaling laws of the structure functions. It is shown that when the structure functions exhibit anomalous scaling, the dissipation correlation function does not decay on length scales that are in the scaling range. The implication of our findings is that the concept of an "inertial range" in which the dissipative terms can be ignored is untenable. The consequences of this mechanism for other cases of possible anomalous scaling in turbulence are discussed.

View PDFchevron_right
Computing the Scaling Exponents in Fluid Turbulence from First Principles: Demonstration of Multiscaling
Victor L'Vov, Anna Pomyalov

Journal of Statistical Physics, 2000

This manuscript is a draft of work in progress, meant for network distribution only. It will be updated to a formal preprint when the numerical calculations will be accomplished. In this draft we develop a consistent closure procedure for the calculation of the scaling exponents ζn of the nth order correlation functions in fully developed hydrodynamic turbulence, starting from first principles. The closure procedure is constructed to respect the fundamental rescaling symmetry of the Euler equation. The starting point of the procedure is an infinite hierarchy of coupled equations that are obeyed identically with respect to scaling for any set of scaling exponents ζn. This hierarchy was discussed in detail in a recent publication [V.S. L'vov and I. Procaccia, Phys. Rev. E, submitted, chao-dyn/970507015]. The scaling exponents in this set of equations cannot be found from power counting. In this draft we discuss in detail low order non-trivial closures of this infinite set of equations, and prove that these closures lead to the determination of the scaling exponents from solvability conditions. The equations under consideration after this closure are nonlinear integro-differential equations, reflecting the nonlinearity of the original Navier-Stokes equations. Nevertheless they have a very special structure such that the determination of the scaling exponents requires a procedure that is very similar to the solution of linear homogeneous equations, in which amplitudes are determined by fitting to the boundary conditions in the space of scales. The re-normalization scale that is necessary for any anomalous scaling appears at this point. The Hölder inequalities on the scaling exponents select the renormalizaiton scale as the outer scale of turbulence L.

View PDFchevron_right
Transition to turbulence scaling in Rayleigh-Bénard convection
Ambrish Pandey

Physical Review E, 2018

If a fluid flow is driven by a weak Gaussian random force, the nonlinearity in the Navier-Stokes equations is negligibly small and the resulting velocity field obeys Gaussian statistics. Nonlinear effects become important as the driving becomes stronger and a transition occurs to turbulence with anomalous scaling of velocity increments and derivatives. This process has been described by V. Yakhot and D. A. Donzis, Phys. Rev. Lett. 119, 044501 (2017) for homogeneous and isotropic turbulence (HIT). In more realistic flows driven by complex physical phenomena, such as instabilities and nonlocal forces, the initial state itself, and the transition to turbulence from that initial state, are much more complex. In this paper, we discuss the Reynolds-number-dependence of moments of the kinetic energy dissipation rate of orders 2 and 3 obtained in the bulk of thermal convection in the Rayleigh-Bénard system. The data are obtained from three-dimensional spectral element direct numerical simulations in a cell with square cross section and aspect ratio 25 by A. Pandey et al., Nat. Commun. 9, 2118 (2018). Different Reynolds numbers 1 Re 1000 which are based on the thickness of the bulk region and the corresponding root-mean-square velocity are obtained by varying the Prandtl number Pr from 0.005 to 100 at a fixed Rayleigh number Ra = 10 5. A few specific features of the data agree with the theory but the normalized moments of the kinetic energy dissipation rate, En, show a non-monotonic dependence for small Reynolds numbers before obeying the algebraic scaling prediction for the turbulent state. Implications and reasons for this behavior are discussed.

View PDFchevron_right
Matter-wave turbulence: Beyond kinetic scaling
Thomas Gasenzer

Physical Review A, 2010

Turbulent scaling phenomena are studied in an ultracold Bose gas away from thermal equilibrium. Fixed points of the dynamical evolution are characterized in terms of universal scaling exponents of correlation functions. The scaling behavior is determined analytically in the framework of quantum field theory, using a nonperturbative approximation of the two-particle irreducible effective action. While perturbative Kolmogorov scaling is recovered at higher energies, scaling solutions with anomalously large exponents arise in the infrared regime of the turbulence spectrum. The extraordinary enhancement in the momentum dependence of long-range correlations could be experimentally accessible in dilute ultracold atomic gases. Such experiments have the potential to provide insight into dynamical phenomena directly relevant also in other present-day focus areas like heavy-ion collisions and early-universe cosmology.

View PDFchevron_right
Generalized scaling in fully developed turbulence
Luca Biferale

Physica D-nonlinear Phenomena, 1996

In this paper we report numerical and experimental results on the scaling properties of the velocity turbulent fields in several flows. The limits of a new form of scaling, named Extended Self Similarity(ESS), are discussed. We show that, when a mean shear is absent, the self scaling exponents are universal and they do not depend on the specific flow (3D homogeneous turbulence, thermal convection , MHD). In contrast, ESS is not observed when a strong shear is present. We propose a generalized version of self scaling which extends down to the smallest resolvable scales even in cases where ESS is not present. This new scaling is checked in several laboratory and numerical experiment. A possible theoretical interpretation is also proposed. A synthetic turbulent signal having most of the properties of a real one has been generated.

View PDFchevron_right
Dynamical scaling and the finite-capacity anomaly in three-wave turbulence
Alan Newell

Physical Review E, 2010

We present a systematic study of the dynamical scaling process leading to the establishment of the Kolmogorov-Zakharov (KZ) spectrum in weak 3-wave turbulence. In the finite capacity case, in which the transient spectrum reaches infinite frequency in finite time, the dynamical scaling exponent is anomalous in the sense that it cannot be determined from dimensional considerations. As a consequence, the transient spectrum preceding the establishment of the steady state is steeper than the KZ spectrum. Constant energy flux is actually established from right to left in frequency space after the singularity of the transient solution. From arguments based on entropy production, a steeper transient spectrum is heuristically plausible. 94.05.Lk Wave turbulence [1] concerns the statistical mechanics of systems containing large numbers of dispersive waves which interact conservatively. Such wave systems occur in a variety of contexts in nature and engineering. Commonly cited examples include gravity waves on the ocean surface, waves in Bose-Einstein condensates and magnetohydrodynamic waves in strongly magnetized plasmas. For a short review of applications see [2]. Often the waves are driven by external forcing which supplies energy (or possibly another conserved quantity such as wave-action) at a scale which is widely separated from the characteristic scale of dissipation. Since interactions among waves are conservative, turbulence results. That is to say, the physics is dominated by the flux of energy between the forcing scale and dissipation scale. This flux is mediated by the wave interactions. Theoretically, wave turbulence is more tractable than its hydrodynamic cousin. In the limit of weak nonlinearity, the theory is asymptotically closed under relatively mild assumptions on the initial wave statistics (see for a review). Asymptotic closure, resulting from the interplay of weak nonlinearity and dispersion, allows a consistent derivation of a kinetic equation describing the long time asymptotics of the frequency-space wave action density, N ω (t) , which in turn, determines the leading order behaviour of all the higher order cumulants in both Fourier and physical spaces. In this article, we limit our discussion to the so-called 3-wave kinetic equation (3WKE) describing cases where the dominant nonlinearity is quadratic and the dispersion relation admits three-wave resonances.

View PDFchevron_right

References (58)

  1. A. N. Kolmogorov, "The Local Structure of Turbulence in In- compressible Viscous Fluid for Very Large Reynolds Num- bers," Proc. R. Soc. A Math. Phys. Eng. Sci. 434, 9-13 (1991).
  2. Uriel Frisch, Turbulence. The legacy of A.N. Kolmogorov (Cam- bridge University Press, 1995).
  3. A. Groisman and V. Steinberg, "Elastic turbulence in a polymer solution flow," Nature 405, 53-55 (2000).
  4. Christopher Dombrowski, Luis Cisneros, Sunita Chatkaew, Raymond E. Goldstein, and John O. Kessler, "Self- Concentration and Large-Scale Coherence in Bacterial Dynam- ics," Phys. Rev. Lett. 93, 098103 (2004).
  5. Luis H. Cisneros, Ricardo Cortez, Christopher Dombrowski, Raymond E. Goldstein, and John O. Kessler, "Fluid dynamics of self-propelled microorganisms, from individuals to concen- trated populations," Exp. Fluids 43, 737-753 (2007).
  6. T. Ishikawa, N. Yoshida, H. Ueno, M. Wiedeman, Y. Imai, and T. Yamaguchi, "Energy Transport in a Concentrated Suspension of Bacteria," Phys. Rev. Lett. 107, 028102 (2011).
  7. Henricus H Wensink, Jörn Dunkel, Sebastian Heidenreich, Knut Drescher, Raymond E Goldstein, Hartmut Löwen, and Julia M Yeomans, "Meso-scale turbulence in living fluids," Proc. Natl. Acad. Sci. U. S. A. 109, 14308-13 (2012).
  8. Jörn Dunkel, Sebastian Heidenreich, Knut Drescher, Henri- cus H. Wensink, Markus Bär, and Raymond E. Goldstein, "Fluid Dynamics of Bacterial Turbulence," Phys. Rev. Lett. 110, 228102 (2013).
  9. Adama Creppy, Olivier Praud, Xavier Druart, Philippa L. Kohnke, and Franck Plouraboué, "Turbulence of swarming sperm," Phys. Rev. E 92, 032722 (2015).
  10. Tim Sanchez, Daniel T N Chen, Stephen J DeCamp, Michael Heymann, and Zvonimir Dogic, "Spontaneous motion in hier- archically assembled active matter," Nature 491, 431-4 (2012).
  11. G. Henkin, S. J. DeCamp, D. T. N. Chen, T. Sanchez, and Z. Dogic, "Tunable dynamics of microtubule-based active isotropic gels," Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 372, 20140142 (2014).
  12. Pau Guillamat, Jordi Ignés-Mullol, and Francesc Sagués, "Taming active turbulence with patterned soft interfaces," Nat. Commun. 8, 564 (2017).
  13. Linnea M. Lemma, Stephen J. DeCamp, Zhihong You, Luca Giomi, and Zvonimir Dogic, "Statistical properties of au- tonomous flows in 2D active nematics," Soft Matter 15, 3264- 3272 (2019).
  14. Amin Doostmohammadi, Sumesh P Thampi, Thuan B Saw, Chwee T Lim, Benoit Ladoux, and Julia M Yeomans, "Cell division: a source of active stress in cellular monolayers," Soft Matter 11, 7328-7336 (2015).
  15. Taeseok Daniel Yang, Hyun Kim, Changhyeong Yoon, Seung- Kuk Baek, and Kyoung J Lee, "Collective pulsatile expan- sion and swirls in proliferating tumor tissue," New J. Phys. 18, 103032 (2016).
  16. C. Blanch-Mercader, V. Yashunsky, S. Garcia, G. Duclos, L. Giomi, and P. Silberzan, "Turbulent Dynamics of Epithe- lial Cell Cultures," Phys. Rev. Lett. 120, 208101 (2018).
  17. Daiki Nishiguchi and Masaki Sano, "Mesoscopic turbulence and local order in Janus particles self-propelling under an ac electric field," Phys. Rev. E 92, 052309 (2015).
  18. Jörn Dunkel, Sebastian Heidenreich, Markus Bär, and Ray- mond E Goldstein, "Minimal continuum theories of structure formation in dense active fluids," New J. Phys. 15, 045016 (2013).
  19. J. Słomka and J. Dunkel, "Generalized Navier-Stokes equations for active suspensions," Eur. Phys. J. Spec. Top. 224, 1349- 1358 (2015).
  20. Robert Großmann, Pawel Romanczuk, Markus Bär, and Lutz Schimansky-Geier, "Vortex Arrays and Mesoscale Turbulence of Self-Propelled Particles," Phys. Rev. Lett. 113, 258104 (2014).
  21. Sebastian Heidenreich, Jörn Dunkel, Sabine H. L. Klapp, and Markus Bär, "Hydrodynamic length-scale selection in mi- croswimmer suspensions," Phys. Rev. E 94, 020601 (2016).
  22. Vasil Bratanov, Frank Jenko, and Erwin Frey, "New class of turbulence in active fluids," Proc. Natl. Acad. Sci. 112, 15048- 15053 (2015).
  23. Martin James, Wouter J. T. Bos, and Michael Wilczek, "Tur- bulence and turbulent pattern formation in a minimal model for active fluids," Phys. Rev. Fluids 3, 061101 (2018).
  24. Jonasz Słomka and Jörn Dunkel, "Spontaneous mirror- symmetry breaking induces inverse energy cascade in 3D active fluids," Proc. Natl. Acad. Sci. U. S. A. 114, 2119-2124 (2017).
  25. Jonasz Słomka, Piotr Suwara, and Jörn Dunkel, "The nature of triad interactions in active turbulence," J. Fluid Mech. 841, 702-731 (2018).
  26. Charles W Wolgemuth, "Collective Swimming and the Dynam- ics of Bacterial Turbulence," Biophys. J. 95, 1564-1574 (2008).
  27. Luca Giomi, M. Cristina Marchetti, and Tanniemola B. Liver- pool, "Complex Spontaneous Flows and Concentration Band- ing in Active Polar Films," Phys. Rev. Lett. 101, 198101 (2008).
  28. Luca Giomi and M. Cristina Marchetti, "Polar patterns in active fluids," Soft Matter 8, 129 (2012).
  29. Francesco Bonelli, Giuseppe Gonnella, Adriano Tiribocchi, and Davide Marenduzzo, "Spontaneous flow in polar active flu- ids: the effect of a phenomenological self propulsion-like term," Eur. Phys. J. E. Soft Matter 39, 1 (2016).
  30. Rajesh Ramaswamy and Frank Jülicher, "Activity induces trav- eling waves, vortices and spatiotemporal chaos in a model ac- tomyosin layer," Sci. Rep. 6, 20838 (2016).
  31. C. Blanch-Mercader and J. Casademunt, "Hydrodynamic insta- bilities, waves and turbulence in spreading epithelia," Soft Mat- ter 13, 6913-6928 (2017).
  32. S.P. Thampi and J.M. Yeomans, "Active turbulence in active nematics," Eur. Phys. J. Spec. Top. 225, 651-662 (2016).
  33. Amin Doostmohammadi, Jordi Ignés-Mullol, Julia M. Yeo- mans, and Francesc Sagués, "Active nematics," Nat. Commun. 9, 3246 (2018).
  34. S. M. Fielding, D. Marenduzzo, and M. E. Cates, "Nonlinear dynamics and rheology of active fluids: Simulations in two di- mensions," Phys. Rev. E 83, 041910 (2011).
  35. L. Giomi, L. Mahadevan, B. Chakraborty, and M. F. Hagan, "Excitable Patterns in Active Nematics," Phys. Rev. Lett. 106, 218101 (2011).
  36. Sumesh P. Thampi, Ramin Golestanian, and Julia M. Yeomans, "Velocity Correlations in an Active Nematic," Phys. Rev. Lett. 111, 118101 (2013).
  37. Sumesh P. Thampi, Ramin Golestanian, and Julia M. Yeomans, "Instabilities and topological defects in active nematics," EPL (Europhysics Lett. 105, 18001 (2014).
  38. Sumesh P Thampi, Ramin Golestanian, and Julia M Yeomans, "Vorticity, defects and correlations in active turbulence," Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 372, 20130366 (2014).
  39. Sumesh P. Thampi, Ramin Golestanian, and Julia M. Yeomans, "Active nematic materials with substrate friction," Phys. Rev. E 90, 062307 (2014).
  40. Luca Giomi, "Geometry and Topology of Turbulence in Active Nematics," Phys. Rev. X 5, 031003 (2015).
  41. Sumesh P. Thampi, Amin Doostmohammadi, Ramin Golesta- nian, and Julia M. Yeomans, "Intrinsic free energy in active nematics," EPL (Europhysics Lett. 112, 28004 (2015).
  42. Ewan J. Hemingway, Prashant Mishra, M. Cristina Marchetti, and Suzanne M. Fielding, "Correlation lengths in hydrody- namic models of active nematics," Soft Matter 12, 7943-7952 (2016).
  43. Amin Doostmohammadi, Tyler N. Shendruk, Kristian Thijssen, and Julia M. Yeomans, "Onset of meso-scale turbulence in ac- tive nematics," Nat. Commun. 8, 15326 (2017).
  44. J. Urzay, A. Doostmohammadi, and J. M. Yeomans, "Multi- scale statistics of turbulence motorized by active matter," J. Fluid Mech. 822, 762-773 (2017).
  45. M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, Madan Rao, and R. Aditi Simha, "Hydrodynamics of soft active matter," Rev. Mod. Phys. 85, 1143-1189 (2013).
  46. J. Prost, F. Jülicher, and J-F. Joanny, "Active gel physics," Nat. Phys. 11, 111-117 (2015).
  47. Frank Jülicher, Stephan W Grill, and Guillaume Salbreux, "Hy- drodynamic theory of active matter," Reports Prog. Phys. 81, 076601 (2018).
  48. Pierre-Gilles de Gennes and Jacques Prost, The Physics of Liq- uid Crystals, 2nd ed. (Oxford University Press, 1993).
  49. R. Aditi Simha and Sriram Ramaswamy, "Hydrodynamic Fluc- tuations and Instabilities in Ordered Suspensions of Self- Propelled Particles," Phys. Rev. Lett. 89, 058101 (2002).
  50. R Voituriez, J F Joanny, and J Prost, "Spontaneous flow transi- tion in active polar gels," Europhys. Lett. 70, 404-410 (2005).
  51. Luca Giomi, Mark J Bowick, Prashant Mishra, Rastko Sknep- nek, and M. Cristina Marchetti, "Defect dynamics in active ne- matics," Philos. Trans. A. Math. Phys. Eng. Sci. 372, 20130365 (2014).
  52. Berta Martínez-Prat, Jordi Ignés-Mullol, Jaume Casademunt, and Francesc Sagués, "Selection mechanism at the onset of ac- tive turbulence," Nat. Phys. 15, 362 (2019).
  53. Tyler N. Shendruk, Amin Doostmohammadi, Kristian Thijssen, and Julia M. Yeomans, "Dancing disclinations in confined ac- tive nematics," Soft Matter 13, 3853-3862 (2017).
  54. Jonasz Słomka and Jörn Dunkel, "Geometry-dependent vis- cosity reduction in sheared active fluids," Phys. Rev. Fluids 2, 043102 (2017).
  55. William H Press, Saul A Teukolsky, William T Vetterling, and Brian P Flannery, Numerical recipes in Fortran 77. The art of scientific computing, 2nd ed. (Cambridge University Press, 1992).
  56. Markus Seeβelberg and Francesco Petruccione, "Numerical in- tegration of stochastic partial differential equations," Comput. Phys. Commun. 74, 303-315 (1993).
  57. Masud Chaichian, Ioan Merches, and Anca Tureanu, Mechan- ics. An intensive course (Springer, 2012).
  58. K Kruse, J F Joanny, F. Jülicher, J Prost, and K Sekimoto, "Generic theory of active polar gels: a paradigm for cytoskele- tal dynamics," Eur. Phys. J. E 16, 5-16 (2005).

Related papers

Nonlocal interactions in hydrodynamic turbulence at high Reynolds numbers: The slow emergence of scaling laws
annick pouquet

Physical Review E, 2008

We analyze the data stemming from a forced incompressible hydrodynamic simulation on a grid of 2048 3 regularly spaced points, with a Taylor Reynolds number of R λ ∼ 1300. The forcing is given by the Taylor-Green flow, which shares similarities with the flow in several laboratory experiments, and the computation is run for ten turnover times in the turbulent steady state. At this Reynolds number the anisotropic large scale flow pattern, the inertial range, the bottleneck, and the dissipative range are clearly visible, thus providing a good test case for the study of turbulence as it appears in nature. Triadic interactions, the locality of energy fluxes, and structure functions of the velocity increments are computed. A comparison with runs at lower Reynolds numbers is performed, and shows the emergence of scaling laws for the relative amplitude of local and non-local interactions in spectral space. The scalings of the Kolmogorov constant, and of skewness and flatness of velocity increments, performed as well and are consistent with previous experimental results. Furthermore, the accumulation of energy in the small-scales associated with the bottleneck seems to occur on a span of wavenumbers that is independent of the Reynolds number, possibly ruling out an inertial range explanation for it. Finally, intermittency exponents seem to depart from standard models at high R λ , leaving the interpretation of intermittency an open problem.

View PDFchevron_right
Scaling Behavior in Turbulence is Doubly Anomalous
Victor L'Vov

Physical Review Letters, 1996

It is shown that the description of anomalous scaling in turbulent systems requires the simultaneous use of two normalization scales. This phenomenon stems from the existence of two independent (infinite) sets of anomalous scaling exponents that appear in leading order, one set due to infrared anomalies, and the other due to ultraviolet anomalies. To expose this clearly we introduce here a set of local fields whose correlation functions depend simultaneously on the the two sets of exponents. Thus the Kolmogorov picture of "inertial range" scaling is shown to fail because of anomalies that are sensitive to the two ends of this range. PACS numbers 47.27.Gs, 47.27.Jv, 05.40.+j  0 = (ρ · ∇ ′ ) 0 ≡ 1 , 2 = (ρ · ∇ ′ ) 2 −

View PDFchevron_right
Structure-function scaling of bounded two-dimensional turbulence
G.H. Keetels

Physical Review E, 2011

Statistical properties of forced two-dimensional turbulence generated in two different flow domains are investigated by numerical simulations. The considered geometries are the square domain and the periodic channel domain, both bounded by lateral no-slip sidewalls. The focus is on the direct enstrophy cascade range and how the statistical properties change in the presence of no-slip boundaries. The scaling exponents of the velocity and the vorticity structure functions are compared to the classical Kraichnan-Batchelor-Leith (KBL) theory, which assumes isotropy, homogeneity, and self-similarity for turbulence scales between the forcing and dissipation scale. Our investigation reveals that in the interior of the flow domain, turbulence can be considered statistically isotropic and locally homogeneous for the enstrophy cascade range, but it is weakly intermittent. However, the scaling of the vorticity structure function indicates a steeper slope for the energy spectrum than the KBL theory predicts. Near the walls the turbulence is strongly anisotropic at all flow scales.

View PDFchevron_right
Scaling laws in turbulence
Martine Le Berre

Chaos: An Interdisciplinary Journal of Nonlinear Science, 2020

View PDFchevron_right
Universality in fully developed turbulence
Detlef Lohse

Physical Review E, 1994

We extend the numerical simulations of She et al. [Phys. Rev. Lett. 70, 3251 (1993)] of highly turbulent flow with 15 ≤ Taylor-Reynolds number Re λ ≤ 200 up to Re λ ≈ 45 000, employing a reduced wave vector set method (introduced earlier) to approximately solve the Navier-Stokes equation. First, also for these extremely high Reynolds numbers Re λ , the energy spectra as well as the higher moments -when scaled by the spectral intensity at the wave number k p of peak dissipation -can be described by one universal function of k/k p for all Re λ . Second, the ISR scaling exponents ζ m of this universal function are in agreement with the 1941 Kolmogorov theory (the better, the large Re λ is), as is the Re λ dependence of k p . Only around k p viscous damping leads to slight energy pileup in the spectra, as in the experimental data (bottleneck phenomenon).

View PDFchevron_right

Related topics

  • Physics
  • Nature Physics
  • Turbulence kinetic energy

    • Cited by

    Inertia Drives a Flocking Phase Transition in Viscous Active Fluids
    rayan chatterjee

    Physical Review X

    How fast must an oriented collection of extensile swimmers swim to escape the instability of viscous active suspensions? We show that the answer lies in the dimensionless combination R ¼ ρv 2 0 =2σ a , where ρ is the suspension mass density, v 0 the swim speed, and σ a the active stress. Linear stability analysis shows that, for small R, disturbances grow at a rate linear in their wave number q and that the dominant instability mode involves twist. The resulting steady state in our numerical studies is isotropic hedgehog-defect turbulence. Past a first threshold R of order unity, we find a slower growth rate, of Oðq 2 Þ; the numerically observed steady state is phase turbulent: noisy but aligned on average. We present numerical evidence in three and two dimensions that this inertia-driven flocking transition is continuous, with a correlation length that grows on approaching the transition. For much larger R, we find an aligned state linearly stable to perturbations at all q. Our predictions should be testable in suspensions of mesoscale swimmers [D. Klotsa, Soft Matter 15, 8946 (2019)].

    View PDFchevron_right
    Machine learning active-nematic hydrodynamics
    Link Morgan

    Proceedings of the National Academy of Sciences

    Hydrodynamic theories effectively describe many-body systems out of equilibrium in terms of a few macroscopic parameters. However, such parameters are difficult to determine from microscopic information. Seldom is this challenge more apparent than in active matter, where the hydrodynamic parameters are in fact fields that encode the distribution of energy-injecting microscopic components. Here, we use active nematics to demonstrate that neural networks can map out the spatiotemporal variation of multiple hydrodynamic parameters and forecast the chaotic dynamics of these systems. We analyze biofilament/molecular-motor experiments with microtubule/kinesin and actin/myosin complexes as computer vision problems. Our algorithms can determine how activity and elastic moduli change as a function of space and time, as well as adenosine triphosphate (ATP) or motor concentration. The only input needed is the orientation of the biofilaments and not the coupled velocity field which is harder to...

    View PDFchevron_right
    Nematic order condensation and topological defects in inertial active nematics
    Roozbeh Saghatchi

    Physical Review E

    Living materials at different length scales manifest active nematic features such as orientational order, nematic topological defects, and active nematic turbulence. Using numerical simulations we investigate the impact of fluid inertia on the collective pattern formation in active nematics. We show that an incremental increase in inertial effects due to reduced viscosity results in gradual melting of nematic order with an increase in topological defect density before a discontinuous transition to a vortex-condensate state. The emergent vortex-condensate state at low enough viscosities coincides with nematic order condensation within the giant vortices and the drop in the density of topological defects. We further show flow field around topological defects is substantially affected by inertial effects. Moreover, we demonstrate the strong dependence of the kinetic energy spectrum on the inertial effects, recover the Kolmogorov scaling within the vortex-condensate phase, but find no evidence of universal scaling at higher viscosities. The findings reveal complexities in active nematic turbulence and emphasize the important cross-talk between active and inertial effects in setting flow and orientational organization of active particles.

    View PDFchevron_right
    Active boundary layers in confined active nematics
    Justine Laurent

    Nature Communications, 2022

    The role of boundary layers in conventional liquid crystals is commonly related to the mesogen anchoring on confining walls. In the classical view, anchoring enslaves the orientational field of the passive material under equilibrium conditions. In this work, we show that an active nematic can develop active boundary layers that topologically polarize the confining walls. We find that negatively-charged defects accumulate in the boundary layer, regardless of the wall curvature, and they influence the overall dynamics of the system to the point of fully controlling the behavior of the active nematic in situations of strong confinement. Further, we show that wall defects exhibit behaviors that are essentially different from those of their bulk counterparts, such as high motility or the ability to recombine with another defect of like-sign topological charge. These exotic behaviors result from a change of symmetry induced by the wall in the director field around the defect. Finally, we suggest that the collective dynamics of wall defects might be described in terms of a model equation for one-dimensional spatio-temporal chaos. In fluid dynamics and soft materials science, boundary layers refer to the part of the flow that is close to a boundary, featuring built-up slip velocities associated to localized profiles of scalar fields, like pressure, temperature, solute concentration or ionic charge density 1,2. Although the length scale spanned by such boundary layers is much smaller than any macroscopic length, the details of the interfacial transport processes entirely control the distant fluid dynamics. Here, we reveal the existence of a new type of boundary layer in a confined Active Nematic (AN) 3 , which we call active boundary layer (ABL). Defects, i. e. regions of undefined local order, is similarly a transversal concept in condensed, both hard and soft, materials. Although normally transitory for systems near equilibrium, defects play a significant role in many contexts, from phase transitions, mediated by defect proliferation 4,5 , to colloid assembly, via defect entanglement in liquid crystal (LC)-based dispersions 6-8. In this latter context, defects refer to singularities in the orientational field that are endowed with topological indices that bear characteristics similar to electric charges. Stressing this resemblance, and expanding the conventional notion of electrified interfaces, we demonstrate that active LCs 3,9,10 engender ABLs that become polarized by accumulating equal-sign topological defects. We experimentally realize two-dimensional ANs by the selfassembly of filamentous bundles of microtubules and kinesin molecular motors at the water/oil interface 11-13 , which form an active ordered film populated by motile topological defects characterized by semi-integer topological indices, or charges 3. Trefoil-like-1/2 defects are passively advected by the flow while comet-like +1/2 defects actively drive the system. Experiments 11,12,14-17 and theoretical models 18-22 show that ANs feature a balanced population of positive and negative semi-integer defects that continuously unbind and recombine, resulting in a turbulent mixing regime 16,23-25. Different from this traditional view, we show here that, under lateral confinement, ANs can feature ABLs that are exclusively populated by negative defects. When analyzed individually, these boundary defects display differences with respect to their bulk counterparts, both in terms of their motility, symmetries, and built-up stresses. Remarkably, we identify recombination events between equal-sign defects residing at the boundary.

    View PDFchevron_right
    Fractal generation in a two-dimensional active-nematic fluid
    Jorge Arteaga

    Chaos: An Interdisciplinary Journal of Nonlinear Science, 2021

    View PDFchevron_right
    580 California St., Suite 400
    San Francisco, CA, 94104
    © 2025 Academia. All rights reserved