adaptive-grid refinement

description7 papers

group0 followers

lightbulbAbout this topic

Adaptive-grid refinement is a computational technique used in numerical simulations to dynamically adjust the resolution of a grid based on the solution's features. This method enhances accuracy and efficiency by refining the grid in regions with high gradients or complex structures while coarsening it in areas with less variation.

lightbulbAbout this topic

Key research themes

1. How can semidefinite programming combined with adaptive grids efficiently find optimal experimental designs in linear models?

This research theme explores the integration of semidefinite programming (SDP) with adaptive grid (AG) refinement techniques to effectively compute optimal continuous experimental designs, particularly in linear statistical models. It addresses the challenges of handling large search spaces in design criteria optimization by adaptively refining grids where important support points for designs lie, ensuring computational efficiency and guaranteed optimality through convex optimization. This theme is crucial for improving the accuracy and cost-effectiveness in experimental planning across scientific domains.

Adaptive grid semidefinite programming for finding optimal designs

by WENG KEE WONG

2022, Statistics and Computing

Key finding: This paper develops an iterative algorithm that combines SDP with adaptive grid methods to locate optimal continuous designs for linear models. By first discretizing the design space coarsely and solving an SDP to obtain an... Read more

articleView Paper downloadDownload

2. What are effective strategies for h- and hp-adaptive mesh refinement in finite element and isogeometric methods to improve accuracy while maintaining mesh admissibility and computational feasibility?

This research theme examines the development and implementation of adaptive mesh refinement (AMR) techniques—both h-refinement (mesh subdivision) and hp-refinement (polynomial order increase)—within finite element (FE) and isogeometric analysis frameworks. These methods aim to concentrate computational resources where solution features exhibit steep gradients or singularities, enhancing accuracy without prohibitive computational cost. Key issues include the foundations of adaptivity for different element types (triangular prisms, hierarchical B-splines), marking and refinement algorithms, and maintaining the admissibility of generated meshes to ensure bounded basis function overlaps and solver efficiency.

Adaptive Semi-Structured Mesh Refinement Techniques for the Finite Element Method

by Ing. Luis E. Garcia Castillo

2023, Applied Sciences

Key finding: This work introduces h-adaptive refinement for triangular prismatic elements within finite element analysis, detailing three steps: error estimation, marking, and refinement. Five marking strategies are compared and adapted... Read more

articleView Paper downloadDownload

Refinement Algorithms for Adaptive Isogeometric Methods with Hierarchical Splines

by Carlotta Giannelli

2021, Axioms

Key finding: The paper proposes refinement algorithms for hierarchical B-spline spaces used in adaptive isogeometric analysis to construct locally graded admissible meshes. The methods rigorously control the interaction of basis functions... Read more

articleView Paper downloadDownload

Adaptive mesh refinements for analyses of 2D linear elasticity problems using the Kriging-based finite element method

by Johanna Handoko

2023, E3S Web of Conferences

Key finding: This study evaluates adaptive mesh refinement strategies within the Kriging-based finite element method (K-FEM) for 2D linear elasticity. Using three error indicators—strain energy error, gradient of effective stresses, and... Read more

articleView Paper downloadDownload

Adaptive Grid Refinement for Convergence Studies

by Michel Visonneau

2023

Key finding: Addressing the challenge of generating nested unstructured hexahedral meshes suitable for verification studies, this work uses metric-based anisotropic adaptive refinement to produce series of meshes with controlled cell size... Read more

articleView Paper downloadDownload

keyboard_arrow_downShow more

3. How can stable and accurate interpolation and discretization frameworks support dynamically evolving time-dependent adaptive mesh refinement in numerical PDE simulations?

This line of research investigates the stability, accuracy, and computational methodologies required for time-dependent adaptive mesh refinement (AMR) where computational grids are dynamically changed during simulation time. It focuses on interpolation operators for transferring solution data between evolving meshes, ensuring stability via inner product preserving operators, and the preservation of formal energy bounds for semi-discretized PDEs. The work encompasses mesh refinement control, the design of finite difference stencils adapting to solutions, and visualization strategies for hierarchical mesh data.

Stable Dynamical Adaptive Mesh Refinement

by Tomas Lundquist

2022, Journal of Scientific Computing

Key finding: This paper formulates a theoretical framework for stable interpolation between dynamically adaptive meshes in time-dependent PDE simulations. By treating mesh interpolation as a transmission problem and employing inner... Read more

articleView Paper downloadDownload

Accurate solution-adaptive finite difference schemes for coarse and fine grids

by Mark H Carpenter

2022, Journal of Computational Physics

Key finding: This work introduces finite difference stencils with coefficients dynamically optimized to minimize truncation errors based on the evolving solution, thereby combining high-order convergence in well-resolved regions with... Read more

articleView Paper downloadDownload

Implementing a Visualization Tool for Adaptive Mesh Refinement Data using VTK

by Terry Ligocki

2023

Key finding: To address the lack of direct support for AMR data visualization in common scientific graphics frameworks, this work develops an extension to the Visualization Toolkit (VTK) capable of handling hierarchical grids at varying... Read more

articleView Paper downloadDownload

Interactive and dynamic control of adaptive mesh refinement with nested hierarchical grids

by James M Hyman

2016

Key finding: This research develops a method combining interactive user steering with solution-adaptive control over AMR based on nested refined grids. A linearized data structure for 1D problems facilitates integration with implicit and... Read more

articleView Paper downloadDownload

keyboard_arrow_downShow more

All papers in adaptive-grid refinement

A computation chain in fluid-structure interaction for marine applications

by Michel Visonneau

2025, HAL (Le Centre pour la Communication Scientifique Directe)

HAL is a multi-disciplinary open access archive for the deposit and dissemination of scientific research documents, whether they are published or not. The documents may come from teaching and research institutions in France or abroad, or... more

descriptionView Paper arrow_downwardDownload

Unstructured Grid Convergence Study

by Emmanuel Guilmineau

2024, HAL (Le Centre pour la Communication Scientifique Directe)

This paper focus on convergence study of CFD prediction using unstructured grid with our in house finite volume unstructured RANSE solver ISIS-CFD. Computations have been performed with different grid sets generated with different... more

descriptionView Paper arrow_downwardDownload

Numerical simulation around a realistic car model with different rear profiles

by Emmanuel Guilmineau

2024, HAL (Le Centre pour la Communication Scientifique Directe)

descriptionView Paper arrow_downwardDownload

A Multi-Fidelity Successive Response Surface Method for Crashworthiness Optimization Problems

by Tjark Siefkes

2023, Applied Sciences

Due to the high computational burden and the high non-linearity of the responses, crashworthiness optimizations are notoriously hard-to-solve challenges. Among various approaches, methods like the Successive Response Surface Method (SRSM)... more

descriptionView Paper arrow_downwardDownload

Hydrofoil Optimization via Automated Multi-Fidelity Surrogate Models

by Frédéric Hauville

2023

Lifting hydrofoils are gaining importance, since they drastically reduce the wetted surface area of a ship hull, thus decreasing resistance. To attain efficient hydrofoils, the geometries can be obtained from an automated optimization... more

descriptionView Paper arrow_downwardDownload

Adaptive Multi-fidelity Surrogate Modelling for High-quality Shape Optimization

by Michel Visonneau

2023, HAL (Le Centre pour la Communication Scientifique Directe)

A multi-fidelity surrogate modelling approach for shape optimization, which relies on adaptive techniques to obtain good performance for a large range of problems, is presented and critically evaluated. Furthermore, an approach to... more

descriptionView Paper arrow_downwardDownload

Hull shape optimisation using multi-fidelity metamodels and adaptive grid refinement

by Michel Visonneau

2023, HAL (Le Centre pour la Communication Scientifique Directe)

descriptionView Paper arrow_downwardDownload

Adaptive Sampling Criteria for Multi-Fidelity Metamodels in CFD-Based Shape Optimization

by Michel Visonneau

2023

The paper presents a study on four adaptive sampling methods of a multifidelity global metamodel for expensive computer simulations. The multi-fidelity approximation is built as the sum of a low-fidelity-trained metamodel and the... more

descriptionView Paper arrow_downwardDownload

Adapt, Adapt, Adapt:: Recent Trends in Multi-fidelity Digital Modelling for Marine Engineering

by Michel Visonneau

2023

The paper presents some recent trends in multi-fidelity digital modelling for marine engineering applications. Digital modelling is achieved by machine learning methods, namely multi-fidelity surrogate models, trained by computational... more

descriptionView Paper arrow_downwardDownload

A multi-fidelity active learning method for global design optimization problems with noisy evaluations

by Michel Visonneau

2023, Engineering with Computers

A multi-fidelity (MF) active learning method is presented for design optimization problems characterized by noisy evaluations of the performance metrics. Namely, a generalized MF surrogate model is used for design-space exploration,... more

descriptionView Paper arrow_downwardDownload

Combined tensor-based refinement criteria for anisotropic mesh adaptation in ship wave simulation

by Michel Visonneau

2023

Anisotropic grid refinement is performed for the simulation of water flow with free-surface waves. For these flows, the refinement criterion must provide refinement at the water surface, to resolve the conservation law which indicates the... more

descriptionView Paper arrow_downwardDownload

Analytical Benchmark Problems for Multifidelity Optimization Methods

by Melike Nikbay

2023, arXiv (Cornell University)

The paper presents a collection of analytical benchmark problems specifically selected to provide a set of stress tests for the assessment of multifidelity optimization methods. In addition, the paper discusses a comprehensive ensemble of... more

Figure 2: Rosenbrock Function: from left to right, f; (highest-fidelity), f2 , and f3 (lowest-fidelity) The three-fidelity levels are shown for two dimensions in Figure 2. 2.3 Shifted-rotated Rastrigin function To address real-world optimization problems, where the landscape of the objective function is usually multi-modal, the Rastrigin function is selected as benchmark. The function is shifted to change the position of the minimum and rotated to change the properties of the function itself within the variable space. The equation of the shifted-rotated Rastrigin function reads as follows

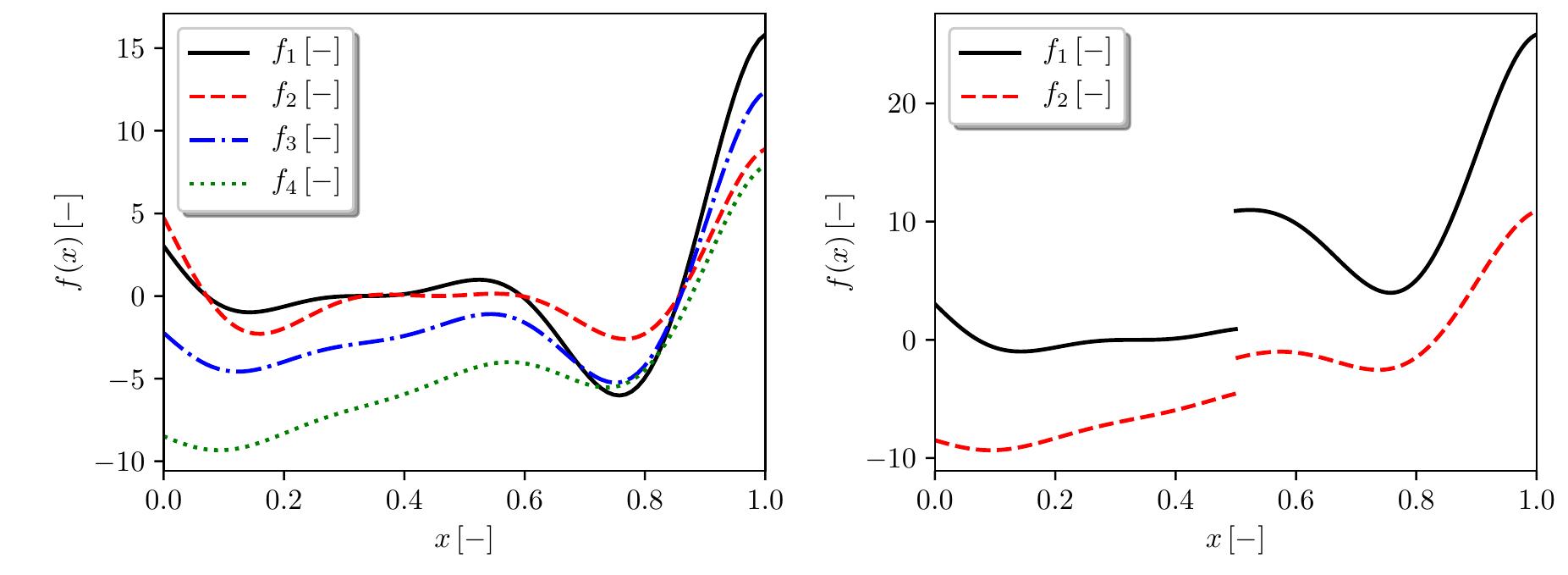
2.4 Heterogeneous function This problem employs heterogeneous non-polynomial analytic functions defined on unit hypercubes (0 < x; < 1 fori = 1,...D) in one, two (taken from [7]), and three dimensions, with low-fidelity functions obtained by using linear additive and multiplicative bridge functions. The benchmark reads

The one- and two-dimensional functions are displayed together with their low-fidelity approxima-

2.5 Coupled Spring-Mass system The proposed problem represents a general coupled spring-mass system. Consider two point masses m, and m2 concentrated at their center of gravity and attached to each other by three springs, that operate according to Hooke’s law with constant k;, kz, and k3. The mass of each spring is negligible and they restore after compression and extension. The masses can slide along a frictionless horizontal surface, while the first and last springs (k, and k3) are attached to fixed walls, as shown in Figure 6.

The equations are justified in the case of all positive variables by observing that the first two springs are elongated by x; and x2 — x1, respectively. The last spring is compressed by x2, which accounts for the minus sign. Eq. (18) can be written as a second-order vector-matrix system

A is a parameter that models the error among the fidelities and can vary between 0 and 1, when A = 0 the low- and high-fidelity equations are the same, while the change between the low-fidelity and high-fidelity models increases as the value of A increases. In this study it is set as A = 0.5, while a; is the coefficient that defines the noise level. The benchmark is defined considering the variable ranges as 0.3 < x; < 1.0 for Vi. For the high-fidelity case a noise level is added to the equation

Table 1: Analytical benchmarks main features een SE The multifidelity benchmark problems are selected to capture fundamental mathematical char- teristics and properties which also mimic real-world engineering problems. The distinguishing athematical features of the selected benchmark problems can be listed as: behaviors, scalability, screpancy type, and noise. Function behaviors include multi-modality, discontinuities, and atypical cal behaviors, that cannot be neglected a priori, especially for real world problems where it could be 1portant to represent the whole variable domain. In particular, multi-modality and discontinuities e challenging from both a modelling and optimization viewpoint. Scalabilty takes into consideration th the function parameterization and the fidelity spectrum. The former is one of the important iteria for the comprehensive assessment of the performance of the multifidelity methods which lables to represent the same parametric function with different input dimensions, whereas the latter useful to demonstrate how the modelling process can be improved depending on the fidelity level railable. This last point is particularly relevant, because its relation with the discrepancy type, that scribes the relation among fidelities. In general, a linear discrepancy is simpler to model than a mnlinear one. For this reason the discrepancy type allows for a deeper assessment of the multifidelity ethods, since the number of fidelities available have to be correlated to the associated discrepancy pe. Finally, in real-world engineering problems, noise may exist, it is undesired but inescapable in e overall response of a system which may exhibit abrupt changes within the solution domain. It is fficult or even impossible to distinguish the individual impact of the noise in the overall response id eliminate it. Thus, the user has to deal with a function with some embedded noise, and is 1portant to asses the ability of multifidelity methods to model a noisy function. Considering all ese mathematical characteristics over the benchmark problems will allow to evaluate the perfor-

Table 3: Summary of multifidelity benchmark values for the evaluation of the goal-sensitive metrics > Concluding Remarks

descriptionView Paper arrow_downwardDownload

Towards Automatic Parameter Selection for Multifidelity Surrogate-Based Optimization

by Michel Visonneau

2023, The 9th Conference on Computational Methods in Marine Engineering (Marine 2021)

The performance of surrogate-based optimization is highly affected by how the surrogate training set is defined. This is especially true for multi-fidelity surrogate models, where different training sets exist for each fidelity. Adaptive... more

descriptionView Paper arrow_downwardDownload

Evaluation of multifidelity surrogate modeling techniques to construct closure laws for drag in shock–particle interactions

by Kyung Choi

2023, Journal of Computational Physics

Please cite this article in press as: O. Sen et al., Evaluation of multifidelity surrogate modeling techniques to construct closure laws for drag in shock-particle interactions,

descriptionView Paper arrow_downwardDownload

Analytical Benchmark Problems for Multifidelity Optimization Methods

by Simone Ficini

2023, arXiv (Cornell University)

descriptionView Paper arrow_downwardDownload

A multi-fidelity active learning method for global design optimization problems with noisy evaluations

by Matteo Diez

2023, Engineering with Computers

Fig.5 Analytical test problems: from top to bottom P, P3, and Py with D = 2 (without noise); from left to right f;, f5, and f; (high-, medium-, and low-fidelity)

Fig. 7, NACA hydrofoil computational grids (G) for ISIS-CFD; from left to right G1 (12.8 k cells), G2 (5.7 k cells), and G3 (3.6 k cells)

Fig.8 The different steps of the ISIS-CFD grid creation for the DTMB 5415 optimization

Fig.9 RoPax ferry grids (bow detail): from left to right G1, G2, G3, and G4

Fig. 10 Analytical test problem P,: from left to right E,, E,, and E,

Fig.11 Analytical test problem P,, from left to right E,, Ep, and E,

Fig. 12 Analytical test problem P;, from left to right E,, Ey, and E,, from top to bottom D = 2,5, 10

Fig. 13 Analytical test problem P,, from left to right E,, E,, and E,, from top to bottom D = 2,5, 10

Fig. 14 NACA hydrofoil, surrogate models and associated prediction uncertainty for D = 1; from left to right N = 1, 2,°

Fig. 15 NACA hydrofoil, surrogate models (top) and associated prediction uncertainty (bottom) for D = 2: from left to right N = 1, 2, 3 vary, even if the final grid topology is the same. This makes it difficult to identify a single cause for the noise. An analysis of the noise behavior in the simulations is given in Fig. 16, which shows the evolution of the drag for a systematic variation of the foil thickness over a small range. The drag on adaptively refined grids is compared with a sys- tematic series of grids created directly by the Hexpress grid generator. These results confirm that for this case, the noise is mostly due to the adaptive refinement procedure, since the grids without adaptation produce a much smoother behavior. These oscillations in the forces are related to small changes in the topology of the adapted grids (i.e. cells, especially in the boundary layers and at the leading edge, which are either refined or not depending on small changes in the hydrofoil geometry). Also, the dynamic adjustment of the foil angle of attack depends, within the tolerances of the algorithm, on the history of the forces. Thus, if the history of the grid refinement is different, the converged angle of attack may However, the noise is proportional to the numerical errors of the simulations: it is most pronounced on the coarsest grid and disappears rapidly as the adapted addition, based on a rough estimati grids become finer. In on of the grid conver- gence for the two series, the adapted grids produce similar accuracy as non-adapted grids with four to five times more cells, thanks to the excellent capturing of the flow around the leading edge on the adapted gri essential to obtain the right forces ds (see Fig. 8), that is for a lifting hydrofoil. Thus, the main benefit of the adaptive refinement here is a gain in efficiency for the CFD simulation. However, the noise is proportional to the numerical errors

Fig. 16 NACA hydrofoil, drag coefficient as a function of ¢ for c =0.0475 and p=0.475. The drawn lines are adapted grids (ADR, G3=3.6 k, G2=5.4 k, G1=11.8 k, and GO=36.3 k cells), the dashed lines are Hexpress-only grids (HEX, G3=14.4 k, G2=24.5 k, G1=37.4 k, and GO=52.8 k cells)

Fig. 17 DTMB 5415, surrogate models prediction (top) and associated uncertainty (bottom); from left to right VN = 1, 2,3 Figure 17 shows the surrogate models with N = 1, 2,3 and the associated prediction uncertainty for the DTMB 5415 optimization problem. The MF method with N = 3 identifies two minimum regions in the neighborhood of (0.15, 0.75) and (0.65, 0.2). However, an inspection of the actual highest-fidelity data reveals that the first optimum may be a numerical artifact of the surrogate model. Nev- ertheless, the active learning procedure correctly ignores the upper-right and lower-left corners, where the predic- tion uncertainty is high, but the objective function value

Fig. 19 DTMB 5415, mass-fraction on the hull-surface; original (top) and optimized (bottom), along with a stern detail (right

Figure 20 (left) compares the pressure distribution along the optimal and the original hull surfaces. The optimized hull has a stronger pressure gradient along the hull, but the low pressure zone is mostly perpendicular to the flow direc- tion, so it has little influence on the drag. Figure 20 (right) shows the wave elevation of the original and optimized hull, Moreover, for this more complex case, while the noise is still related to topology changes in the adapted grids, it is possible to identify distinct sources for the noise. For the lowest-fidelity data, the noise is mostly associated with mod- ifications in the position and the smearing of the wave sys- tem. For example, Fig. 22 (left) shows random fluctuations

Fig. 18 DTMB 5415, comparison of hull shapes

Fig. 20 DTMB 5415, comparison of the original (top) and optimized (bottom) hull shapes; hull-surface pressure (left) and wave elevation pat- tern (right)

Fig.23 DTMB 5145, stern wave pattern: from top to bottom X, = —0.85, —0.825, —0.8, —0.8, from left to right G3, G2, G1 The transom is oriented normal to the flow, so even a small change in wetted surface here has a large influence on

Fig.22 DTMB 5415, bow wave: from top to bottom x, = —0.85, —0.825, —0.8, from left to right G3, G2, G1 in the thickness and the position of the volume fraction dis- continuity in the first trough and the shoulder wave. Since the amount of wetted surface has a large influence on the drag, these changes in the waves explain the oscillations in the forces. Figure 22 (center and right) shows that this perturbation behaves like the noise for the hydrofoil: the finer the grid, the smaller the oscillations. The stern wave crest in Fig. 23 shows similar oscillations. The gradient change in the fine grid solutions is explained by the stern wave too (see Fig. 23, right): a topology change occurs at Xz = —0.825 close to the stern, where a double wave ridge with a small wetted patch on the transom is replaced by a

Fig. 24 RoPax ferry, MF surrogate prediction (top) and associated uncertainty (bottom)

Fig.25 RoPax ferry, original (black lines) and optimized (blue- dashed lines) shapes with the free-surface line (FS)

Fig. 26 RoPax ferry, non-dimensional hull-surface pressure and wave patterns. Colors represent non-dimensional pressure level:

Fig. 27 RoPax ferry, non-dimensional wave patterns. Colors repre- sent non-dimensional wave elevation

Table 1 Analytical benchmark problems by several local minima and adjacent regions of strong gradients and flatness, as shown in Figs. 4 and 5. Further- more, the different fidelity levels are modeled to never have a coincident global minimum among them. Finally, P,and P, are arbitrarily scalable in the number of dimen- sions, and P, also in the number of fidelities.

Test D N CC Median[E,]% Median [E; 1% Median [E,]% Median[7,] Median[7] Median [73]

Finally, even in the Hexpress-only grids, jumps in the drag can be observed when the topology of the grids changes. However, these jumps are less frequent than for the on the history of the forces. Thus, if the history of the grid

Fig. 1 Example of MF surrogate model with N = 2 (without noise)

Fig. 2. Example of the active learning method using one fidelity with- out noise: (left) shows the initial surrogate model with the associated prediction uncertainty and training set; (right) shows the position of the new training point and the new surrogate model prediction and its uncertainty The identification of the new training points is based on the LCB sampling method [7] with equal weight for the function value and the prediction uncertainty (see Fig. 2). It aims to find points with large prediction uncertainty and small objective function value. Accordingly, LCB iden- tifies new training points by minimizing the acquisition function y(x) basis function (RBF) surrogate models, defined by a sto- chastic tuning parameter, z ~ unif[1, 3]:

descriptionView Paper arrow_downwardDownload

Coarse-Grid Computational Fluid Dynamic (CG-CFD) Error Prediction using Machine Learning

by Nam Đinh

2022

Despite the progress in high performance computing, Computational Fluid Dynamics (CFD) simulations are still computationally expensive for many practical engineering applications such as simulating large computational domains and highly... more

descriptionView Paper arrow_downwardDownload

Coarse-Grid Computational Fluid Dynamics (CG-CFD) Error Prediction using Machine Learning

by Nam Đinh

2022, arXiv: Fluid Dynamics

descriptionView Paper arrow_downwardDownload

An Adaptive N Fidelity Metamodel for Design and Operational Uncertainty Space Exploration of Complex Industrial Problems

by Michel Visonneau

2022, CIMNE

An adaptive N-fidelity (NF) metamodel is presented for the solution of simulationbased design optimization and uncertainty quantification problems. A multi-fidelity approximation is built by an additive correction of a low-fidelity... more

descriptionView Paper arrow_downwardDownload

A Multi-Fidelity Active Learning Method for Global Design Optimization Problems with Noisy Evaluations

by Riccardo Pellegrini

2022

descriptionView Paper arrow_downwardDownload

An Investigation into the Use of Ducktail at Transom Stern to Reduce Total Ship Resistance

by I Ketut Aria Pria Utama

2022, IPTEK Journal of Proceedings Series

Abstract In this study it is aimed to investigate the application of ducktail at transom stern to reduce total resistance using Computational Fluid Dynamics (CFD).

descriptionView Paper arrow_downwardDownload

Resource Aware Multifidelity Active Learning for Efficient Optimization

by Michele Garraffa

2022

Traditional methods for black box optimization require a considerable number of evaluations which can be time consuming, unpractical, and often unfeasible for many engineering applications that rely on accurate representations and... more

descriptionView Paper arrow_downwardDownload

A Multi-Fidelity Active Learning Method for Global Design Optimization Problems with Noisy Evaluations

by Riccardo Pellegrini

2022

descriptionView Paper arrow_downwardDownload

Unsteady numerical simulations of downwind sails

by Frédéric Hauville

2021

Modelling the wind, sail and rig interactions on a sailing yacht is a complex subject, because the quality of simulation depends on the accuracy of both structural and fluid simulations which strongly interact. Moreover, the sails are... more

descriptionView Paper arrow_downwardDownload

AN ADAPTIVE N -FIDELITY METAMODEL FOR DESIGN AND OPERATIONAL-UNCERTAINTY SPACE EXPLORATION OF COMPLEX INDUSTRIAL PROBLEMS

by Andrea Serani and

2019, VIII International Conference on Computer Methods in Marine Engineering

An adaptive N-fidelity (NF) metamodel is presented for the solution of simulation-based design optimization and uncertainty quantification problems. A multi-fidelity approximation is built by an additive correction of a low-fidelity... more

Figure 1: N-fidelity adaptive sampling procedure.

Figure 2: Analytical test problem with different number of fidelities N.

where € is the position along the chord, c the chord length, ye the mean camber line, p the location of the maximum camber, m the maximum camber value, and y; the half thickness Figure 3: NACA 4-digit hydrofoil.

Figure 4: NACA hydrofoil computational grids.

The hydrodynamics performance of the RoPax is assessed by the unsteady RANSE code yxnavis developed at CNR-INM. It is based on finite volume scheme, with variable co-located at cell centers. Turbulent stresses are taken into account by the Boussinesq hypothesis, with Spallart-Almaras turbulence model. Free-surface effects are taken into account by a single-phase level-set algorithm. Wall-functions are not adopted, therefore y* = 1 is ensured on the wall. On solid walls, the velocity is set equal to zero and zero normal gradient is enforced on the pressure field; at the (fictitious) inflow boundary, velocity is set to the undisturbed flow value and the pressure is extrapolated from the inside; the dynamic pressure is set to zero at the outflow, whereas the velocity is extrapolated from inner points. On the top boundary, which remains always in the air region, fluid dynamic quantities are extrapolated from inside. Chimera overlapping grid capabilities are used, the numerical solutions are computed by means of a full multi grid-full approximation scheme (FMG-FAS), with four grid levels (from coarser to finer: G4, G3, G2, and G1), each obtained from the next finer grid with a refinement ratio equal to 2, resulting in 6; = 0.125 and 6g = 0.0625. In the FMG—FAS approximation procedure, the

Figure 6: Analytical test problem: convergences of (a) NRMSE, (b) objective function minimum, and (c) the number of the highest-fidelity evaluations versus the sampling procedure iterations. The performance of the adaptive NF metamodel is assessed in terms of convergence of the normalized root mean square error (NRMSBE), the objective function minimum, and the number of highest-fidelity evaluations, as shown in Fig.6.

Figure 7: NACA hydrofoil: N-fidelity metamodel prediction and associated uncertainty, with N = 1, 2, and 3 from left to right. Black squares, red circles, and green stars are the 2 = 1, 2, and 3 fidelity training sets. Yellow triangles is the minimum position.

Figure 8: NACA hydrofoil: verified optimum convergence versus the normalized computational cost evaluations are clustered in three corners. Furthermore, in the latter case the uncertainty of the prediction is significantly higher than for the N = 1 case, suggesting the presence of numerica noise. Finally, for N = 3 the contour plot of the drag coefficient and the uncertainty lool smoother than for N = 2. This suggests a regularization effect stemming from the use of a mid. evel fidelity. At each iteration the predicted minimum is verified through an highest-fidelity simulation. Fig. 8 shows the convergence of the verified objective function. It is worth noting that the NF metamodel converges faster for both N = 2 and 3. Table 2 summarizes, the training sets size, the normalized cost, the maximum uncertainty of the prediction, the coordinates o! the predicted minimum of the Cp, the predicted minimum, its verification, the prediction error and the improvement with respect to the original configuration. It is worth noting that fo1

Figure 9: RoPax ferry: model-scale total resistance versus operational uncertainty (Froude number). N =1, 2, and 3 fidelity metamodels. The NF metamodel for UQ is assessed through statistical estimation of the expected value (EV) and standard deviation (SD) of the total resistance, Rr. The training of the NF metamodel is performed considering at most 4 high-fidelity evaluations. The results are compared to the available highest-fidelity CFD data. Figure 9 shows the MF prediction of the total resistance versus the Froude number, with N =1, 2, and 3. It is worth noting that the increase of N improves the MF prediction. Table 3 summarizes the training sets size, the expected value, standard deviation, and associate errors ( E) for N = 1, 2, and 3. It is worth noting that the MF metamodel with N = 3 achieves better results than using N = 1 and 2. Furthermore, for N =3 only three evaluations of the highest-fidelity are performed.

Table 1: Analytical test problem. 4 NACA HYDROFOIL SHAPE OPTIMIZATION PROBLEM This problem addresses the drag minimization of a NACA four-digit airfoil. The following minimization problem is solved

Table 2: Summary of the adaptive NF metamodel performance on the NACA hydrofoil SBDO problem N = 3 the number of highest-fidelity evaluations decreases compared to N = 1 and 2. Similar improvements are achieved using N = 1, 2, and 3.

Table 3: Summary of the adaptive NF metamodel performance on the RoPax UQ problem.

descriptionView Paper arrow_downwardDownload