Dihedral Groups

Cubic power graph of dihedral group D n having order 2n and identity element e, Γ cpg (D n) is a finite, simple, undirected graph for which two different vertices d 1 , d 2 ∈ D n are adjacent if and only if d 1 d 2 = d 3 or d 2 d 1 = d 3 for some d ∈ D n with d 3 ̸ = e. In this research, conditions on n under which Γ cpg (D n) is planar, are calculated. Also conditions on n under which Γ cpg (D n) is Hamiltonian, are calculated. It is also shown that Γ cpg (D n) is not an Eulerian graph. A polynomial that counts how many different ways there are to color a graph with a specific number of colors is called a chromatic polynomial. We have calculated the chromatic polynomial of Γ cpg (D n) when gcd(n, 3) = 1. Also chromatic polynomial of almost complete graph obtained by deleting k number of non-adjacent edges is obtained. Spectral graph theory is a branch of mathematics that examines a graph's characteristics in relation to its characteristic polynomial, eigenvalues, and eigenvectors of related matrices, such as its adjacency matrix, Laplacian matrix or degree based matrices. Characteristic polynomials of degree based matrices such as Laplacian matrix, Signless Laplacian matrix, Maximum matrix, Minimum matrix and Greatest common divisor degree matrix of Γ cpg (D n) when gcd(n, 3) = 1.

The study of graphs associated with algebraic structures has become an influential approach in understanding both the combinatorial and algebraic properties of groups. In this paper, we focus on a special class of graphs known as prime coprime graphs constructed from the dihedral groups D 2n , a family of non-abelian finite groups of order 2n. The prime coprime graph, denoted Ω D2n , is defined with the vertex set consisting of the non-identity elements of D 2n , where two distinct vertices are adjacent whenever the greatest common divisor of their orders is a prime number. The primary aim of this research is to examine the spectral properties of Ω D2n , with a focus on the graph energy, defined as the sum of the absolute values of the eigenvalues of its adjacency matrix. We construct the adjacency matrix of Ω D2n for cases where n is either a power of a prime or a product of two distinct primes. Through direct computation and spectral analysis, we determine the eigenvalues and calculate the energy of the graph. Additionally, we explore the relationship between the energy and the spectral radius. Our findings provide new insights into the spectral behavior of non-commutative algebraic graphs and contribute to the broader theory of graph energies. While the study is restricted to specific cases of n, it opens pathways for generalizations to other classes of groups. These results may have further implications in algebraic combinatorics, coding theory, and the spectral classification of finite groups.

This paper aims at treating a study on Sylow theorem of different algebraic structures as groups, order of a group, subgroups, along with the associated notions of automorphisms group of the dihedral groups, split extensions of groups and vector spaces arises from the varying properties of real and complex numbers. We must have used the Sylow theorems of this work when it's generalized. Here we discuss possible subgroups of a group in different types of order which will give us a practical knowledge to see the applications of the Sylow theorems. In algebraic structures, we deal with operations of addition and multiplication and in order structures, those of greater than, less than and so on. It is through the study of Sylow theorems that we realize the importance of some definitions as like as the exact sequences and split extensions of groups, Sylow p-subgroup and semi-direct product. Thus it has been found necessary and convenient to study these structures in detail. In situations, where it was found that a given situation satisfies the basic axioms of structure and having already known the properties of that structure. Finally, we find out possible subgroups of a group in different types of order for abelian and non-abelian cases.

In this paper, we provide a group-theoretic computer-free construction of some 10-arcs in PG(2; q) which have the dihedral group of order 6 as stabiliser and which have similar geometrical properties to some complete 10-arcs of minimum size in PG(2; q); for q = 17; 23: Having at one's disposal such 10-arcs in PG(2; q); for almost all q; we analyse, by means of a computer search, some possibilities of completing them and we prove that such 10-arcs give a way of determining several examples of very small complete arcs in PG(2; q):

In this paper we investigate the total negation of rigidity namely anti-rigidity. A topological space X is anti-rigid if there is no rigid subspace of X with more than one point. In particular, we establish the relationships of anti-rigidity with metric spaces, scattered spaces and ordered sets with order topology etc.

Scholars have recently become interested in the importance of the reflexive and Birkhoff polytopes in a variety of applications in our daily lives. Unanswered queries and educated guesses abound in reflexive polytopes. We use the free sum and product for reflexives polytopes, as well as the product for two Birkhoff polytopes, and the proven theorem to get specific unimodality results. The computations are acquired via algorithms.

The probability that the commutator of two group elements is equal to a given element has been introduced in literature few years ago. Several authors have investigated this notion with methods of the representation theory and with combinatorial techniques. Here we illustrate that a wider context may be considered and show some structural restrictions on the group.

The present paper is a note on the relative tensor degree of finite groups. This notion generalizes the tensor degree, introduced recently in literature, and allows us to adapt the concept of relative commutativity degree through the notion of nonabelian tensor square. We show two inequalities, which correlate the relative tensor degree with the relative commutativity degree of finite groups.

We call a real multi-dimensional array a tensor for short. In enumerating vertices of the polytopes of stochastic tensors, different approaches have been used: (1) Combinatorial method via Latin squares; (2) Analytic (topological) approach by using hyperplanes; (3) Computational geometry (polytope theory) approach; and (4) Optimization (linear programming) approach. As all these approaches are worthy of consideration and investigation in the enumeration problem, various bounds have been obtained. This note is to compare the existing upper bounds arose from different approaches.

Let G = (V,E) be a (p, q)-graph. A bijection f : E → {1, 2, 3, . . . , q} is called an edge-prime labeling if for each edge uv in E, we have GCD(f+(u), f+(v)) = 1 where f+(u) = ∑ uw∈E f(uw). Moreover, a bijection f : E → {1, 2, 3, . . . , q} is called a semi-edge-prime labeling if for each edge uv in E, we have GCD(f+(u), f+(v)) = 1 or f+(u) = f+(v). A graph that admits an edge-prime (or a semi-edgeprime) labeling is called an edge-prime (or a semi-edge-prime) graph. In this paper we determine the necessary and/or sufficient condition for the existence of (semi-) edge-primality of bipartite and tripartite graphs.

We describe a class of facets of the polytope of convex combinations of the collection of even n × n permutation matrices. As a consequence, we prove the conjecture of Brualdi and Liu [4] that the number of facets of the polytope is not bounded by a polynomial in n.

We described and studied the concept of maximum degree based vertex graceful labeling graph with odd labeling on edges in this approach. It is a particular type of labeling vertex of a graph G with p vertices and q edges if there exists a bijection f from the edge set to the set {1, 3, 5,. .. , (2q − 1)} so that the induced mapping f * : V → {0, 1, 2,. .. , (2q − 1)} which is given by f * (u) = f (uv) /uv ∈ E(G) , where is maximum degree of G, [ ] denotes the integral part. Keywords Crown graph • Degree • Edge • Maximum • Odd • Vertex 1 Introduction Graph labeling [1-3] is an assignment of integers to the vertices or edges or both subject to certain conditions. Graph labeling is extremely useful in various areas such as coding theory, mobile, optimal circuits' layout, graph decomposition problems, communication networks, and designing. Nowadays, graph labeling is fascinated by researchers to work on it.

An edge magic total labeling of graph with p vertices and q edges is a bijection from the set of vertices and edges to 1, 2, 3,…,p+qsuch that for every edge the sum of the label of the edges and the label of its two end vertices are constant. And if the sum is distinct it is said to be an edge antimagic total labeling. In this paper, we exhibit edge antimagic total labeling on graph structure for various arithmetic progression.

We present some examples and remarks which may be helpful to those who are dealing with an abstract algebra or a first semester group theory course. Alternating groups, dihedral groups, and symmetric groups of small orders are treasure troves of elementary examples and counter examples concerning groups.

The concept of subgroup commutativity degree of a finite group G is arising interest in several areas of group theory in the last years, since it gives a measure of the probability that a randomly picked pair (H, K) of subgroups of G satisfies the condition HK = KH. In this paper, a stronger notion is studied and relations with the commutativity degree are found.

A digraph D with p vertices and q arcs is labeled by assigning a distinct integer value g(v) from f0, 1, :::, qg to each vertex v. The vertex values, in turn, induce a value g(u, v) on each arc (u, v) where g(u, v) ¼ (g(v) À g(u)) (mod q þ 1) If the arc values are all distinct then the labeling is called a graceful labeling of digraph. In this survey article, we have collected results that we could find interesting on graceful labeling of digraphs.

We calculate the local groups of germs associated with the higher dimensional R. Thompson groups nV . For a given n ∈ N ∪ {ω}, these groups of germs are free abelian groups of rank r , for r ≤ n (there are some groups of germs associated with nV with rank precisely k for each index 1 ≤ k ≤ n). By Rubin’s theorem, any conjectured isomorphism between higher dimensional R. Thompson groups induces an isomorphism between associated groups of germs. Thus, if m = n the groups mV and nV cannot be isomorphic. This answers a question of Brin.

We initiate the study of analogues of symmetric spaces for the family of finite dihedral groups. In particular, we investigate the structure of the automorphism group, characterize the involutions of the automorphism group, and determine the fixed-group and symmetric space of each automorphism.

This paper aims at treating a study on Sylow theorem of different algebraic structures as groups, order of a group, subgroups, along with the associated notions of automorphisms group of the dihedral groups, split extensions of groups and vector spaces arises from the varying properties of real and complex numbers. We must have used the Sylow theorems of this work when it's generalized. Here we discuss possible subgroups of a group in different types of order which will give us a practical knowledge to see the applications of the Sylow theorems. In algebraic structures, we deal with operations of addition and multiplication and in order structures, those of greater than, less than and so on. It is through the study of Sylow theorems that we realize the importance of some definitions as like as the exact sequences and split extensions of groups, Sylow p-subgroup and semi-direct product. Thus it has been found necessary and convenient to study these structures in detail. In situations, where it was found that a given situation satisfies the basic axioms of structure and having already known the properties of that structure. Finally, we find out possible subgroups of a group in different types of order for abelian and non-abelian cases.

Representation theory is a study of real realizations of the axiomatic systems of abstract algebra. It originated in the study of permutation groups, and algebras of matrices. Representation theory has important applications in physics and chemistry. This research focuses on finite metacyclic groups. The classification of finite metacyclic groups is divided into three types which are denoted as Type I, Type II and Type III. For any group, the number of possible representative sets of matrices is infinite, but they can all be reduced to a single fundamental set, called the irreducible representations of the group. Irreducible representation is actually the nucleus of a character table and is of great importance in chemistry. In this research, the irreducible representation of finite metacyclic groups of class two of order 16 are found using two methods, namely the Great Orthogonality Theorem Method and Burnside Method.

A graph G of order p and size q is called (a,d)-edge-antimagic total if there exists a one-to-one and onto mapping f from ∪ , , … , such that the edge weights , ∈ form an AP progression with first term 'a' and common difference 'd'. The graph G is said to be Super (a,d)-edge-antimagic total labeling if the , , … , . In this paper we obtain Super (a,d)-edge-antimagic properties of certain classes of graphs, including Fans graph, Single fan graph, Half Kite graph and Ambrela graph.

We describe various classes of infinitely presented groups that are condensation points in the space of marked groups. A well-known class of such groups consists of finitely generated groups admitting an infinite minimal presentation. We introduce here a larger class of condensation groups, called infinitely independently presentable groups, and establish criteria which allow one to infer that a group is infinitely independently presentable. In addition, we construct examples of finitely generated groups with no minimal presentation, among them infinitely presented groups with Cantor–Bendixson rank 1, and we prove that every infinitely presented metabelian group is a condensation group.

In [Baumeister, H., Nill, Paffenholz, On permutation polytopes, Adv. Math. 222 (2009), 431-452 / arXiv:0709.1615] we conjectured a characterization of subgroups H of a permutation group G so that, on the level of permutation polytopes, P(H) is a face of P(G). Here we present the embarrassingly simple proof of this conjecture.

In this paper we give a combinatorial view on the adjunction theory of toric varieties. Inspired by classical adjunction theory of polarized algebraic varieties we define two convex-geometric notions: the Q-codegree and the nef value of a rational polytope P. We define the adjoint polytope P^(s) as the set of those points in P, whose lattice distance to every facet of P is at least s. We prove a structure theorem for lattice polytopes P with high Q-codegree. If P^(s) is empty for some s < 2/(dim(P)+2), then the lattice polytope P has lattice width one. This has consequences in Ehrhart theory and on polarized toric varieties with dual defect. Moreover, we illustrate how classification results in adjunction theory can be translated into new classification results for lattice polytopes.

In this work the basic concept of reflexive polytope and Gorenstein polytope and Fano with some theorems about them are given. Three standard binary operations on polytopes which are: the cartesian product (×), the direct sum (⊕) and the free join(⋈) are examined. Finally techniques are used to prove the conjecture |V(P)| ≤ 6 of the maximal number of vertices for a simplicial reflexive polytopes of even dimension. ‫ﻟﻤﺘ‬ ‫اﻟﺮؤوس‬ ‫ﻣﻦ‬ ‫ﻋﺪد‬ ‫اﻛﺒﺮ‬ ‫اﻻﻧﻌﻜﺎﺳﻲ‬ ‫اﻟﺴﻄﻮح‬ ‫ﻌﺪد‬ ‫اﻟﺨﻼﺻﺔ‬ ‫اﻻﻧﻌﻜﺎﺳﻲ‬ ‫اﻟﺴﻄﻮح‬ ‫ﻟﻤﺘﻌﺪد‬ ‫اﻻﺳﺎﺳﯿﺔ‬ ‫اﻟﻤﻔﺎھﯿﻢ‬ ‫ﺑﻌﺾ‬ ‫ﻋﺮﻓﻨﺎ‬ ‫اﻟﺒﺤﺚ‬ ‫ھﺬا‬ ‫ﻓﻲ‬ ‫اﻟﺴﻄﻮح‬ ‫ﻣﺘﻌﺪد‬ ‫و‬ ‫ﺟﻮرﻧﺴﺘﯿﻦ‬ ‫ﻣﺘﻌﺪد‬ ‫ﻋﻠﻰ‬ ‫اﻻﺑﺘﺪاﺋﯿﺔ‬ ‫اﻟﻌﻤﻠﯿﺎت‬ ‫ﻣﻦ‬ ‫وﺛﻼث‬ ,‫ﻓﺎﻧﻮ‬ ‫اﻟﺴﻄﻮح‬ ‫وﻣﺘﻌﺪد‬ ‫اﻟﺴﻄﻮح‬ ‫ات‬ ‫اﻟﺪﯾﻜﺎرﺗﻲ‬ ‫اﻟﻀﺮب‬ ‫وھﻲ‬) (× ‫و‬ , free sum) ⨁ ‫و‬ , (free join) (⋈ ‫اﺳﺘﺨﺪﻣﻨﺎ‬ ‫واﺧﯿﺮا‬ .‫اﺧﺘﺒﺎرھﺎ‬ ‫ﺗﻢ‬ ‫ﺗﻜﻨﯿﻚ‬ ‫ﻷﺛﺒﺎت‬ ‫اﻟﻤﻔﺘﻮﺣﺔ‬ ‫اﻟﻤﺴﺄﻟﺔ‬ |V(P)| ≤ 6 ‫ﻷﻛﺒﺮ‬ .‫اﻻﻧﻌﻜﺎﺳﻲ‬ ‫اﻟﺴﻄﻮح‬ ‫ﻟﻤﺘﻌﺪد‬ ‫اﻟﺮؤوس‬ ‫ﻣﻦ‬ ‫ﻋﺪد‬ INTRODUCTION he reflexive polytopes P ⊆ R were introduced by Victor Batyrev in the context of a ...

Motivated by the model theory of higher order logics, a certain kind of topological spaces had been introduced on ultraproducts. These spaces are called ultratopologies. Ultratopologies provide a natural extra topological structure for ultraproducts and using this extra structure some preservation and characterization theorems had been obtained for higher order logics. The purely topological properties of ultratopologies seem interesting on their own right. Here we present the solutions of two problems of Gerlits and Sagi. More concretely we show that (1) there are sequences of finite sets of pairwise different cardinality such that in their certain ultraproducts there are homeomorphic ultratopologies and (2) one can always find a dense set in an ultratopology whose cardinality is strictly smaller than the cardinality of the ultraproduct, provided that the factors of the corresponding ultraproduct are finite.

Some new results on metric ultraproducts of finite simple groups are presented. Suppose that G is such a group, defined in terms of a non-principal ultrafilter ω on N and a sequence (G i ) i∈N of finite simple groups, and that G is neither finite nor a Chevalley group over an infinite field. Then G is isomorphic to an ultraproduct of alternating groups or to an ultraproduct of finite simple classical groups. The isomorphism type of G determines which of these two cases arises, and, in the latter case, the ω-limit of the characteristics of the groups G i . Moreover G is a complete path-connected group with respect to the natural metric on G. Résumé. Nous présentons de nouveaux résultats relatifs aux ultraproduits des groupes finis simples. Soit G un tel groupe, associé à un ultrafiltre ω sur N et une suite (G i ) i∈N de groupes finis simples, et supposons que G n'est ni fini ni un groupe de Chevalley sur un corps infini. Un tel groupe G est alors isomorphe soit à un ultraproduit de groups alternés, soit à un ultraproduit de groupes finis simples classiques. La classe d'isomorphisme de G nous permet de distinguer ces deux cas, et dans le second cas, de déterminer le ω-limite des charactéristiques des groupes G i . Le groupe G est de plus complet et connexe par arcs pour la métrique naturelle sur G.

Let G = (V (G), E(G), F (G)) be a simple, finite, connected, plane graph with the vertex set V (G), the edge set E(G) and the face set F (G). A labeling of type (1, 1, 1) assigns labels from the set {1, 2,. .. , |V (G)| + |E(G)| + |F (G)|} to the vertices, edges and faces of a plane graph G, such that each vertex, edge and face receives exactly one label and each number is used exactly once as a label. Moreover, the labeling is called super if the vertices are lebaled with the smallest numbers. The weight of a face under the labeling of type (1, 1, 1) is sum of labels of the face itself and vertices and edges surrounding that face. A labeling of a plane graph is called d-antimagic if for every positive integer s the set of weights of all s-sided faces is W s ={a s , a s + d,. .. , a s + (ν s − 1)d} for some integers a s and d ≥ 0, where ν s is the number of the s-sided faces. In this paper we study (super) d-antimagic labeling of type (1, 1, 1) for some strong face plane graphs.

This paper deals with certain edge labelings of graphs. After having introduced the concepts of a weak antimagic graph and an Egyptian magic graph, the authors showed that every connected graph of order 23 is weakly antimagic and proved some interesting relations between the different edge labelings.

A super edge-magic labeling of a graph G=(V,E) of order p and size q is a bijection f:V ∪E→{i}p+qi=1 such that: (1) f(u)+f(uv)+f(v)=k for all uv∈E; and (2) f(V )={i}pi=1. Furthermore, when G is a linear forest, the super edge-magic labeling of G is called strong if it has the extra property that if uv∈E(G) , u′,v′ ∈V (G) and dG (u,u′ )=dG (v,v′ )<+∞, then f(u)+f(v)=f(u′ )+f(v′ ). In this paper we introduce the concept of strong super edge-magic labeling of a graph G with respect to a linear forest F, and we study the super edge-magicness of an odd union of nonnecessarily isomorphic acyclic graphs. Furthermore, we find exponential lower bounds for the number of super edge-magic labelings of these unions. The case when G is not acyclic will be also considered.

We describe various classes of infinitely presented groups that are condensation points in the space of marked groups. A well-known class of such groups consists of finitely generated groups admitting an infinite minimal presentation. We introduce here a larger class of condensation groups, called infinitely independently presentable groups, and establish criteria which allow one to infer that a group is infinitely independently presentable. In addition, we construct examples of finitely generated groups with no minimal presentation, among them infinitely presented groups with Cantor-Bendixson rank 1, and we prove that every infinitely presented metabelian group is a condensation group.

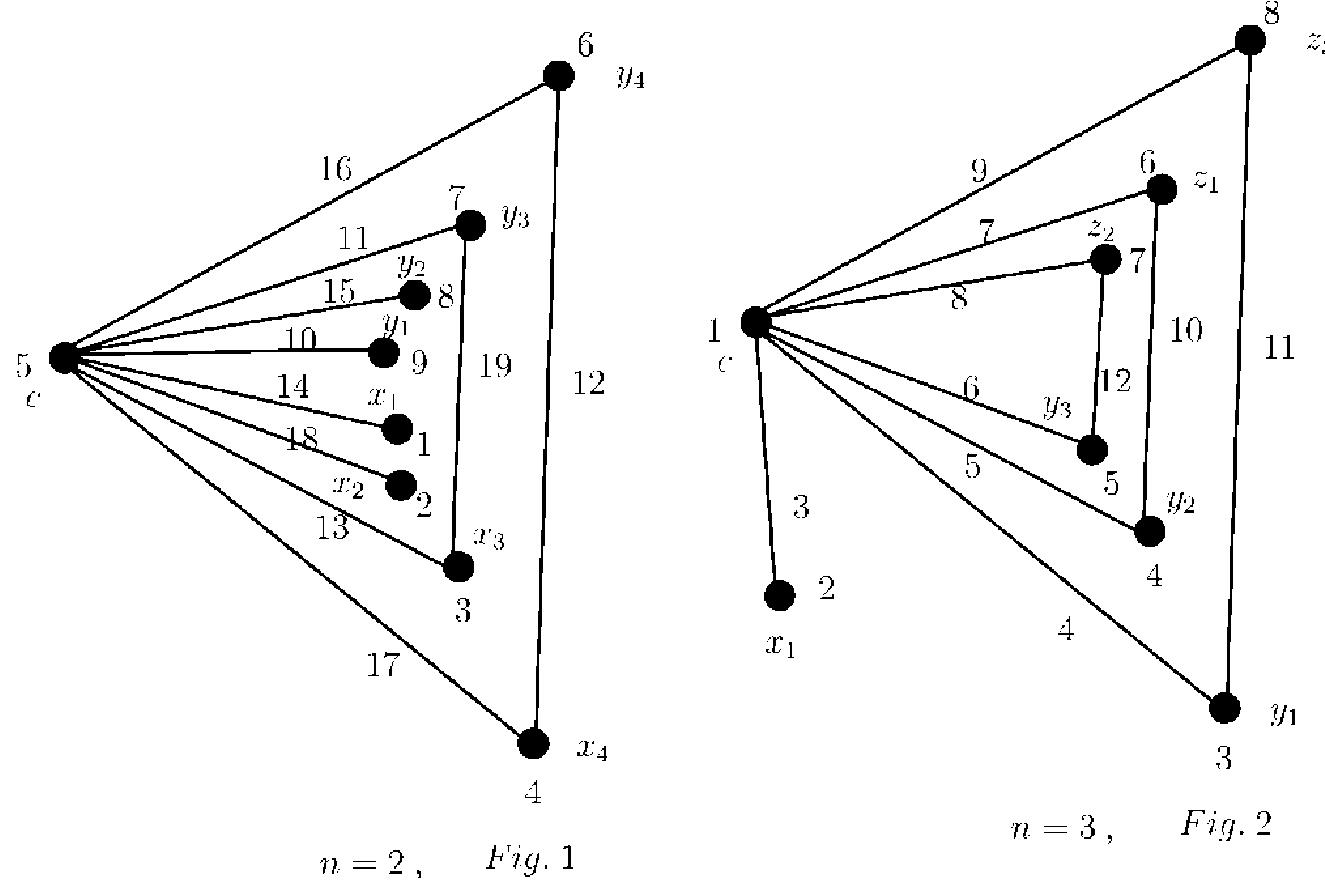
A Cayley digraph is a digraph constructed from a group Γ and a generating subset S of Γ. It is denoted by Cay D (Γ, S). In this paper, we prove for any finite group Γ and a generating subset S of Γ, that Cay D (Γ, S) admits a super vertex (a, d)-antimagic labeling depending on d and |S|. We provide algorithms for constructing the labelings.

We initiate the study of analogues of symmetric spaces for the family of finite dihedral groups. In particular, we investigate the structure of the automorphism group, characterize the involutions of the automorphism group, and determine the fixed-group and symmetric space of each automorphism.

Let G = (V,E) be a (p, q)-graph. A bijection f : E → {1, 2, 3, . . . , q} is called an edge-prime labeling if for each edge uv in E, we have GCD(f+(u), f+(v)) = 1 where f+(u) = ∑ uw∈E f(uw). Moreover, a bijection f : E → {1, 2, 3, . . . , q} is called a semi-edge-prime labeling if for each edge uv in E, we have GCD(f+(u), f+(v)) = 1 or f+(u) = f+(v). A graph that admits an edge-prime (or a semi-edgeprime) labeling is called an edge-prime (or a semi-edge-prime) graph. In this paper we determine the necessary and/or sufficient condition for the existence of (semi-) edge-primality of bipartite and tripartite graphs.

When adjustment costs are present, cyclical preference and technology heterogeneities in a product’s markets induce cycles in production. We exploit cyclic and dihedral group invariances in an industry’s cost technology to describe these patterns. We show when equilibrium cyclical pricing and production patterns are ordered according to demand patterns. Our approach allows us to identify periods when prices may fall below unit costs, net of adjustment costs. Social welfare preferences over cyclical demand and supply heterogeneities are identified. We study the particulars of cycle dynamics when demand is linear and adjustment costs are quadratic. The analysis is developed for when external trade is impossible and when it is possible.

Let G = (V,E) be a (p, q)-graph. A bijection f : E → {1, 2, 3, . . . , q} is called an edge-prime labeling if for each edge uv in E, we have GCD(f+(u), f+(v)) = 1 where f+(u) = ∑ uw∈E f(uw). Moreover, a bijection f : E → {1, 2, 3, . . . , q} is called a semi-edge-prime labeling if for each edge uv in E, we have GCD(f+(u), f+(v)) = 1 or f+(u) = f+(v). A graph that admits an edge-prime (or a semi-edgeprime) labeling is called an edge-prime (or a semi-edge-prime) graph. In this paper we determine the necessary and/or sufficient condition for the existence of (semi-) edge-primality of bipartite and tripartite graphs.

A Cayley digraph is a digraph constructed from a group Γ and a generating subset S of Γ. It is denoted by CayD(Γ, S). In this paper, we prove for any finite group Γ and a generating subset S of Γ, that CayD(Γ, S) admits a super vertex (a, d)-antimagic labeling depending on d and |S|. We provide algorithms for constructing the labelings.

A Cayley digraph is a digraph constructed from a group Γ and a generating subset S of Γ. It is denoted by CayD(Γ, S). In this paper, we prove for any finite group Γ and a generating subset S of Γ, that CayD(Γ, S) admits a super vertex (a, d)-antimagic labeling depending on d and |S|. We provide algorithms for constructing the labelings.

This collection was compiled by Christian Haase and Bruce Reznick from problems presented at the problem sessions, and submissions solicited from the participants of the AMS/IMS/SIAM summer Research Conference on Integer points in polyhedra.

In this note we investigate the convex hull of n×n-permutation matrices corresponding to the symmetry group of a regular n-gon. We give their complete facet description. As an application, we show that they are Gorenstein polytopes, and determine their h *-vectors.

A permutation polytope is the convex hull of a group of permutation matrices. In this paper we investigate the combinatorics of permutation polytopes and their faces. As applications we completely classify permutation polytopes in dimensions 2,3,4, and the corresponding permutation groups up to a suitable notion of equivalence. We also provide a list of combinatorial types of possibly occuring faces

In this note we investigate the convex hull of those $n \times n$-permutation matrices that correspond to symmetries of a regular $n$-gon. We give the complete facet description. As an application, we show that this yields a Gorenstein polytope, and we determine the Ehrhart $h^*$-vector.

In [Baumeister, H., Nill, Paffenholz, On permutation polytopes, Adv. Math. 222 (2009), 431-452 / arXiv:0709.1615] we conjectured a characterization of subgroups H of a permutation group G so that, on the level of permutation polytopes, P(H) is a face of P(G). Here we present the embarrassingly simple proof of this conjecture.

Unimodular triangulations of lattice polytopes and their relatives arise in algebraic geometry, commutative algebra, integer programming and, of course, combinatorics. Presumably, "most" lattice polytopes do not admit a unimodular triangulation. In this article, we survey which classes of polytopes are known to have unimodular triangulations; among them some new classes, and some not so new which have not been published elsewhere. We include a new proof of the classical result by Knudsen-Munford-Waterman stating that every lattice polytope has a dilation that admits a unimodular triangulation. Our proof yields an explicit (although doubly exponential) bound for the dilation factor.

It is known that the underlying spaces of all abelian quotient singularities which are embeddable as complete intersections of hypersurfaces in an affine space can be overall resolved by means of projective torus-equivariant crepant birational morphisms in all dimensions. In the present paper we extend this result to the entire class of toric l.c.i.-singularities. Our proof makes use of Nakajima's classification theorem and of some special techniques from toric and discrete geometry.

A permutation polytope is the convex hull of a group of permutation matrices. In this paper we investigate the combinatorics of permutation polytopes and their faces. As applications we completely classify ≤ 4-dimensional permutation polytopes and the corresponding permutation groups up to a suitable notion of equivalence. We also provide a list of combinatorial types of possibly occuring ≤ 4-faces of permutation polytopes.

An antimagic labeling of a graph with q edges is a bijection from the set of edges to the set of positive integers {1, 2,. .. , q} such that all vertex weights are pairwise distinct, where the vertex weight of a vertex is the sum of the labels of all edges incident with that vertex. A graph is antimagic if it has an antimagic labeling. In this paper, we provide antimagic labelings for a family of generalized pyramid graphs.