On Numerical Radius Inequalities for Operator Matrices
2019, Numerical Functional Analysis and Optimization
https://doi.org/10.1080/01630563.2018.1549073Abstract
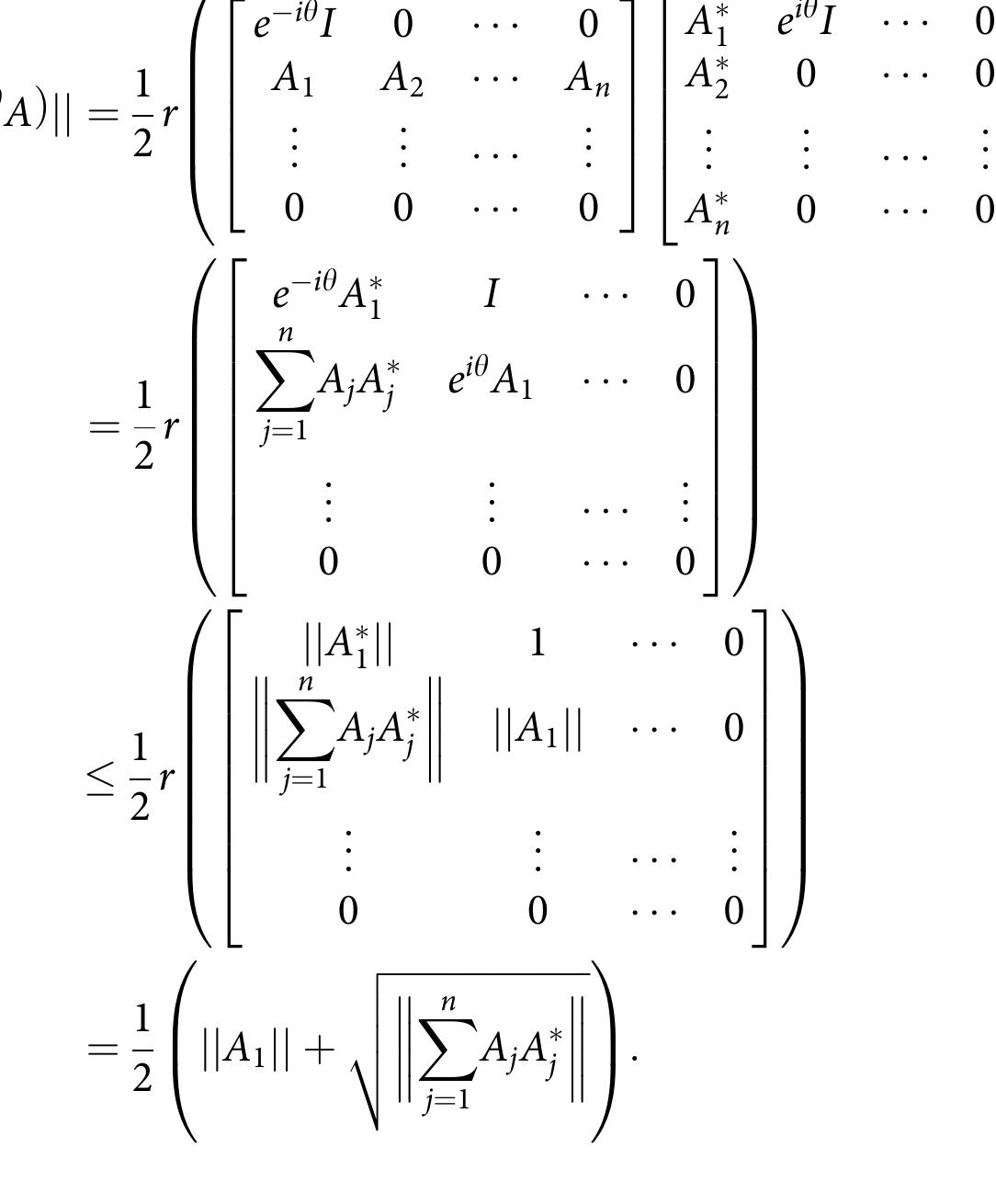
The aim of this article is to prove several new numerical radius inequalities for n  n operator matrices on a Hilbert space. Let H 1 ; H 2 ;. .. ; H n be complex Hilbert spaces, and let T ¼ ½T ij be an n  n operator matrix with T ij 2 BðH j ; H i Þ. Among other inequalities, it shown that ARTICLE HISTORY
References (12)
- Abu-Omar, A., Kittaneh, F. (2015). Numerical radius inequalities for n  n operator matrices. Linear Algebra Appl. 468:18-26. DOI: 10.1016/j.laa.2013.09.049.
- Gustafson, K. E., Rao, D. K. M. (1997). Numerical Range. New York: Springer.
- Halmos, P. R. (1982). A Hilbert Space Problem Book, 2nd ed. New York: Springer.
- Hirzallah, O., Kittaneh, F., Shebrawi, K. (2011). Numerical radius inequalities for certain 2 Â 2 operator matrices. Integr. Equ. Oper. Theory 71(1):129-147. DOI: 10.1007/s00020-011-1893-0.
- Hirzallah, O., Kittaneh, F., Shebrawi, K. (2012). Numerical radius inequalities for 2 Â 2 operator matrices. Studia Math. 210(2):99-115. DOI: 10.4064/sm210-2-1.
- Horn, R. A., Johnson, C. R. (1991). Topics in Matrix Analysis. Cambridge: Cambridge University Press.
- Hou, J. C., Du, H. K. (1995). Norm inequalities of positive operator matrices. Integr. Equ. Oper. Theory. 22(3):281-294. DOI: 10.1007/BF01378777.
- Kittaneh, F. (2003). A numerical radius inequality and an estimate for the numerical radius of the Frobenius companion matrix. Studia Math. Math. 158(1):11-17. DOI: 10.4064/sm158-1-2.
- Ostrovski, S. (2016). Sup and max properties of the numerical radius of operators in Banach spaces, numer. Funct. Anal. Optim. 37:492-498. DOI: 10.1080/ 01630563.2015.1115771
- Shebrawi, K. (2017). Numerical radius inequalities for certain operator matrices II. Linear Algebra Appl. 523:1-12. DOI: 10.1016/j.laa.2017.02.019.
- Uhlig, F. (2009). Geometric computation of the numerical radius of a matrix. Numer. Algor. 52(3):335-353. DOI: 10.1007/s11075-009-9276-1.
- Yamazki, T. (2007). On upper and lower bounds of the numerical radius and an equality condition. Studia Math. 178:83-89. DOI: 10.4064/sm178-1-5
 hanane guelfen
hanane guelfen