Academia.eduAcademia.edu

Outline

Title
Abstract
FAQs
Figures
Objectives
Multi-Objective Analysis
Performance Criteria and Objective Function
Final Objective Function
Application and Results
Fuzzy Objective Functions
Stochastic Analysis (1) Markov Chain
Conclusion
References
All Topics
Engineering
Petroleum Engineering

Multi-objective storage reservoir operation under uncertainty

Profile image of Paulo Sergio Dias ChavesPaulo Sergio Dias Chaves

2003, 京都大学防災研究所年報. B= Disaster Prevention …

Abstract

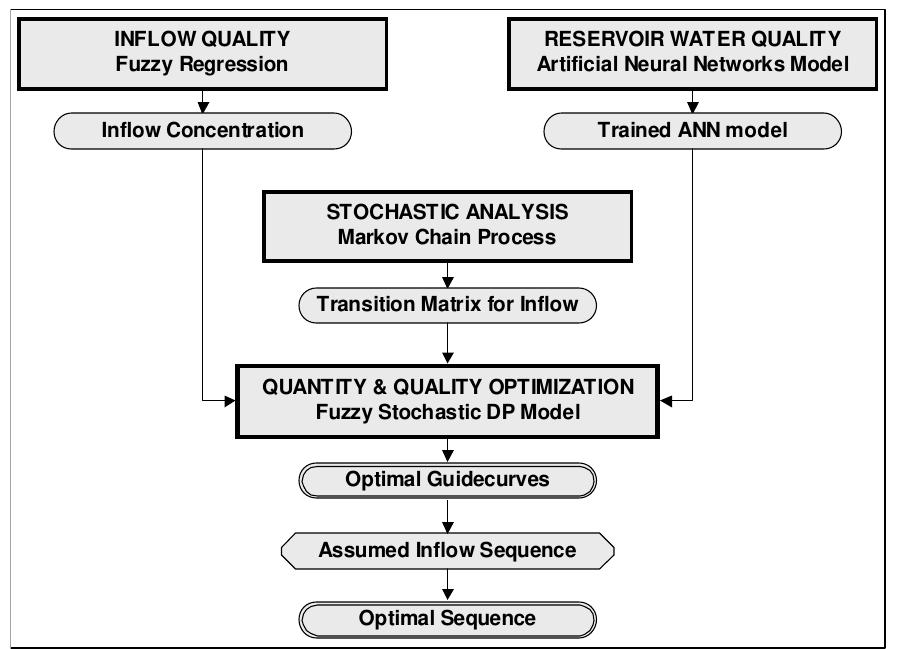
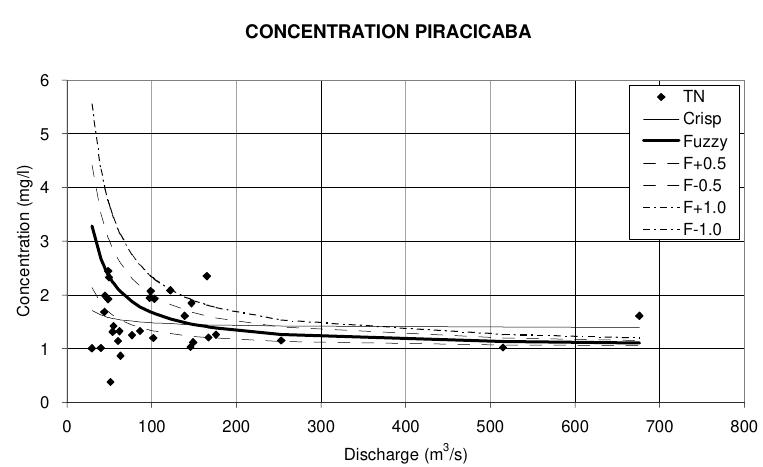
Water quantity and quality are considered to be the main driving forces the reservoir operation. Barra Bonita reservoir, located in the southeast region of Brazil, is chosen as the case study for the application of the proposed methodology. Herein, optimization and artificial intelligence (AI) techniques are applied in the simulation and operation of the reservoir. A fuzzy stochastic dynamic programming model (FSDP) is developed for calculating the optimal operation procedures. Optimization is applied to achieve multiple fuzzy objectives. Markov chain technique is applied to handle the stochastic characteristics of river flow. Water quality analysis is carried out using an artificial neural network model. Organic matter and nutrient loads are modeled as a function of river discharge through the application of a fuzzy regression model based on fuzzy performance functions. The obtained results show that the proposed methodology provides an effective and useful tool for reservoir operation.

FAQs

sparkles

AI

What novel methods are used for reservoir operation under uncertainty?add

The study employs fuzzy set theory and dynamic programming to optimize multi-objective reservoir operations, improving management under uncertainty. Traditional techniques like goal programming are compared to fuzzy methods for greater flexibility in handling imprecise objectives.

How does water quality impact reservoir management decisions?add

The paper highlights that water quality variables significantly affect decisions on water allocation for multiple uses, such as irrigation and recreation. Poor water quality can lead to eutrophication, posing further challenges in resource optimization.

What challenges are associated with water quality data in reservoir studies?add

Limited and infrequent observational data restrict the ability to model complex water quality phenomena effectively, resulting in potential inaccuracies. For example, only 24 observations collected over several years were available for analyzing the Barra Bonita reservoir.

How does the application of artificial neural networks enhance water quality modeling?add

The ANN model, preferred over physical models, simplifies the prediction of water quality by reducing computational demands associated with complex parameter estimation. It utilizes genetic algorithms for training, allowing for a more robust simulation despite limited data availability.

What are the implications of multi-objective optimization in reservoir operations?add

Integrating multiple objectives, such as environmental quality and economic efficiency, complicates reservoir management but leads to more sustainable outcomes. The proposed fuzzy multi-objective fuzzy regression approach provides a structured means to evaluate conflicting objectives in real-time decision-making.

Figures (31)
Fig. 1.1 Storage and water quality single outlet, and quality within the reservoir.
Fig. 1.1 Storage and water quality single outlet, and quality within the reservoir.
research are given in the following sections. Fig. 2.1 Proposed methodology for the water quantity
research are given in the following sections. Fig. 2.1 Proposed methodology for the water quantity
Fig. 1.2 Basic components of the Barra Bonita inflow and release act as key factors on the system behavior.
Fig. 1.2 Basic components of the Barra Bonita inflow and release act as key factors on the system behavior.
Fig. 2.2 Modeling the Barra Bonita system
Fig. 2.2 Modeling the Barra Bonita system
Fig. 3.2: Location of Barra Bonita reservoir the Tieté River can be seen in Fig. 3.2.
Fig. 3.2: Location of Barra Bonita reservoir the Tieté River can be seen in Fig. 3.2.
Fig. 3.1 Schematic profile of the Barra Bonita dam storage levels and elevations is presented in Fig 3.1.
Fig. 3.1 Schematic profile of the Barra Bonita dam storage levels and elevations is presented in Fig 3.1.
Fig. 4.1 Basic structure of the ANN water quality
Fig. 4.1 Basic structure of the ANN water quality
ANN model with GA training is shown in Fig. 4.2. Fig. 4.2 Flowchart for the overall model construction
ANN model with GA training is shown in Fig. 4.2. Fig. 4.2 Flowchart for the overall model construction
Fig. 4.3c Results for DO after training Fig. 4.3b Results for chlorophyll after training
Fig. 4.3c Results for DO after training Fig. 4.3b Results for chlorophyll after training
Fig. 4.3a Results for phosphorous after training
Fig. 4.3a Results for phosphorous after training
used in the training process.
used in the training process.
Fig. 5.2 Membership for the fuzzy number A(a, b, c)
Fig. 5.2 Membership for the fuzzy number A(a, b, c)
Fig. 5.5a BOD load into Tiete River Fig. 5.4b TN concentration of Piracicaba River
Fig. 5.5a BOD load into Tiete River Fig. 5.4b TN concentration of Piracicaba River
Fig. 5.3a BOD load into Piracicaba river
Fig. 5.3a BOD load into Piracicaba river
Fig. 5.3b TN loads into Piracicaba river
Fig. 5.3b TN loads into Piracicaba river
Fig. 5.4a BOD concentration of Piracicaba River
Fig. 5.4a BOD concentration of Piracicaba River
Fig. 5.6a BOD concentrations of Tiete River Fig. 5.5b TN load into Tiete River
Fig. 5.6a BOD concentrations of Tiete River Fig. 5.5b TN load into Tiete River
Fig. 5.6b TN concentrations of Tiete River
Fig. 5.6b TN concentrations of Tiete River
Fig. 6.1 Fuzzy membership functions for flow of release and produced energy, respectively It is very important, particularly in the case of
Fig. 6.1 Fuzzy membership functions for flow of release and produced energy, respectively It is very important, particularly in the case of
Fig. 6.2 Fuzzy membership functions for water can be found in Bollman and Marques (2000). quality evaluation within the reservoir
Fig. 6.2 Fuzzy membership functions for water can be found in Bollman and Marques (2000). quality evaluation within the reservoir
Fig. 6.4 Guidecurves for the month of November for the month of November is showed in Fig. 6.4.
Fig. 6.4 Guidecurves for the month of November for the month of November is showed in Fig. 6.4.
Fig. 7.5a Optimized storage for low load situation large variation of release values.
Fig. 7.5a Optimized storage for low load situation large variation of release values.
Fig. 7.5b Optimized storage for high load situation
Fig. 7.5b Optimized storage for high load situation
Fig. 7.7a Results of flow stabilization fuzzy data collection process. hydropower generation, respectively.
Fig. 7.7a Results of flow stabilization fuzzy data collection process. hydropower generation, respectively.
Fig. 7.6a Results of TP for high load situation
Fig. 7.6a Results of TP for high load situation
Fig. 7.6b Results of TP for high load situation
Fig. 7.6b Results of TP for high load situation
Fig. 7.7b Results for the hydropower fuzzy evaluation
Fig. 7.7b Results for the hydropower fuzzy evaluation

Related papers

1 Development of Fuzzy Reservoir Operation Policies Using Genetic Algorithm
Banafsheh Zahraie

2014

Abstract: This study is focused on developing an integrated optimization-simulation model to develop the operation policies for a multi-purpose reservoir. Objective function of the optimization model is considered to be a linear function of reliability, resiliency, and vulnerability of river-reservoir systems. Genetic Algorithm (GA) is used to solve the optimization model in which the coefficients of the reservoir operation policy equations are considered as the decision variables. These coefficients are formulated in the form of fuzzy numbers to better capture the variations in releases and water demands. Due to significant variations of agricultural water demands in different months and years, a water demand time series is considered as one of the inputs of the optimization model. Zayandeh-rud River-reservoir system in central part of Iran is considered as the case study. Results of this study have shown that the developed algorithm can significantly reduce the time and costs of m...

View PDFchevron_right
Optimal operation of a multi-purpose reservoir using neuro-fuzzy technique
mayank mukund

Water Resources Management, 2009

Present paper is aimed to develop operation policy for a multi-purpose reservoir using Neuro-Fuzzy technique in an efficient way. Ramganga reservoir behind Ramganga dam, Kalagarh, India has been considered as a study reservoir. The developed policy minimizes the damage due to floods and droughts and determines optimum releases against demands for domestic supply, irrigation and hydropower generation for monsoon and non-monsoon periods. Three Fuzzy Rule Based (FRB) models for monsoon period and three for non monsoon period have been developed and tested. Actual releases have been used to formulate the general operation fuzzy rules. Releases computed from all developed models using Fuzzy Mamdani (FM) and ANFIS (Adaptive Neuro-Fuzzy Interactive System) -Grid and Cluster have been compared and it was found that ANFIS-cluster gives the best results but FM is more users friendly. For any expected inflow, reservoir level and demand, release can be calculated using developed GUI windows of the models.

View PDFchevron_right
FUZZY DYNAMIC PROGRAMMING MODEL FOR OPTIMAL OPERATION OF A MULTIPURPOSE RESERVOIR
SRIDHARA REDDY Bandagunda

Optimal operation of reservoir has been an active area of research for many years. Various techniques have been developed and adopted for reservoir operation incorporating the uncertainty due to stochastic nature of inflows and demands. However there is not much literature reported on models incorporating uncertainty caused due to imprecise goals and objectives. In the present paper a fuzzy optimization model is presented for optimal operation of a multipurpose reservoir. Fuzzy optimization model has the capability to incorporate the uncertainty involved in the objectives and variable demands, and fuzzy rules are relatively easy to explain and understand. In the present study fuzzy dynamic programming model is employed for developing ten daily operating rules for optimal operation of a reservoir, namely Hirakud reservoir on River Mahanadi in the State of Orissa in India.

View PDFchevron_right
Automated fuzzy decision and control system for reservoir management
Alberto Cavallo

Journal of Water Supply: Research and Technology—AQUA, 2013

Traditional approaches to the management of an artificial reservoir involve the use of linear, dynamic, nonlinear or stochastic programming. Hence a purely model-based approach would be extremely difficult and thus, recently, a large number of papers devoted to the solution of reservoir management problems based on fuzzy logic approaches have appeared. In this work, two management problems of a reservoir are addressed with fuzzy logic: the definition of the water flow to supply to the user, a typical decision problem; and the regulation of the dam gate, which is a typical control problem. Both problems have been integrated in an Automated Fuzzy Decision and Control System (AFDCS) that is able to identify the ordinary and drought operating conditions. Fuzzy rules are developed from a database derived from the traditional experience of operators and they have been optimized with a genetic algorithm. Two cost functionals are used, able to weight user's desiderata (water demand) with water waste (water spills and evaporation). Three strategies are developed for a case study and are validated in different scenarios, using Monte Carlo simulations and worst case situations. Results show a good performance of AFDCS to alleviate the consequences of drought and to control of the dam gate.

View PDFchevron_right
Optimal Reservoir Operation Considering the Water Quality Issues: Application of Adaptive Neuro-Fuzzy Inference Systems (ANFIS)
Reza Kerachian

World Environmental and Water Resource Congress 2006, 2006

In this study, an algorithm combining a water quality simulation model and a deterministic/stochastic conflict resolution technique is developed for determining optimal reservoir operating rules. As different decision makers and stakeholders are involved in reservoir operation, the Nash ...

View PDFchevron_right
Optimal reservoir operation using fuzzy approach
D Nagesh Kumar

Proce. of Int. Conf. on Civil Engrg., …, 2001

View PDFchevron_right
Development of Fuzzy Reservoir Operation Policies Using Genetic Algorithm
Banafsheh Zahraie

2007

This study is focused on developing an integrated optimization-simulation model to develop the operation policies for a multi-purpose reservoir. Objective function of the optimization model is considered to be a linear function of reliability, resiliency, and vulnerability of river-reservoir systems. Genetic Algorithm (GA) is used to solve the optimization model in which the coefficients of the reservoir operation policy equations

View PDFchevron_right
Reservoir Operation Using a Dynamic Programming Fuzzy Rule–Based Approach
K. Ponnambalam

Water Resources Management, 2005

A dynamic programming fuzzy rule-based (DPFRB) model for optimal operation of reservoirs system is presented in this paper. In the first step, a deterministic dynamic programming (DP) model is used to develop the optimal set of inflows, storage volumes, and reservoir releases. These optimal values are then used as inputs to a fuzzy rule-based (FRB) model to establish the general operating policies in the second step. Subsequently, the operating policies are evaluated in a simulation model. During the simulation step, the parameters of the FRB model are optimized after which the algorithm gets back to the second step in a feedback loop to establish the new set of operating rules using the optimized parameters. This iterative approach improves the value of the performance function of the simulation model and continues until the satisfaction of predetermined stopping criteria. This method results in deriving the operating policies, which are robust against the uncertainty of inflows. These policies are derived by using long-term synthetic inflows and an objective function that minimizes its variance. The DPFRB performance is tested and compared to a model, which uses the commonly used multiple regression-based operating rules. Results show that the DPFRB performs well in terms of satisfying the system target performances and computational requirements.

View PDFchevron_right
Development of Reservoir Operation Policies Using Integrated Optimization-Simulation Approach
Banafsheh Zahraie

Journal of Agricultural Science and Technology, 2010

This study is focused on developing an integrated optimization-simulation based genetic algorithm model (IOSGA) to develop the operational policies for a multipurpose reservoir system. The objective function of the optimization model is considered to be a linear function of Reliability (Rel), Resiliency (Res), and Vulnerability (Vul) of the riverreservoir system. Genetic Algorithm (GA) is employed to solve the optimization model in which the coefficients of reservoir operation policy equations are considered as decision variables. These coefficients are formulated in the form of fuzzy numbers to be able to capture the variations in releases and in water demands. Due to significant variations of agricultural water demands during different months and years, a water demand time series is considered as one of the inputs of the optimization model. Zayandeh-Rud Riverreservoir system, in central part of Iran, is considered the case study. The results of the proposed approach are compared with those of the classic three cyclic algorithm in which the reservoir releases are the decision variables of the optimization model and the IOSGA model in which the coefficients of reservoir operation policies are considered to be classic (non-fuzzy) numbers. The results of the study indicated that the developed algorithm can significantly reduce the time and costs of modeling efforts and the run-time of the GA model, while it has also improved the overall performance of the system in terms of Rel, Res, and maximum Vulnerability (Vul Max) and the coefficient of efficiency (CE) and standard error (SE).

View PDFchevron_right
Fuzzy Logic Model for Optimal Operation of Darbandikhan Reservoir, Iraq
Hekmat M. Ibrahim

International Journal of Design & Nature and Ecodynamics, 2021

The operating system of a reservoir is a significant contributor to its success in water resources management. For a multipurpose reservoir, an ideal operating system determines output characteristics that take account of all objectives. In this study, a new model to optimize Darbandikhan reservoir system operation in Iraq is proposed, based on a fuzzy logic controller. The aim of the new system is to maximize hydropower production while satisfying all downstream water demands. The proposal was tested on flow and other data in 324 monthly time steps, from January 1992 to December 2018, using a simulation model based on the Simulink technique of MATLAB software. Trial and error showed that membership functions of the Gaussian shape were most appropriate. For comparison purposes, Discrete Differential Dynamic Programming (DDDP), Nonlinear Programming (NLP) and Linear Programming (LP) optimization models were developed and applied to operate the reservoir. The results for turbine operation show that, relative to actual power produced, average monthly hydropower generation is increased by 32.2% (fuzzy logic), 51.4% (DDDP), 29.3% (NLP), 27.4% (LP). Although the dynamic programming method generated more hydropower, the fuzzy logic controller avoided complex optimization procedures, making it more flexible and more acceptable to operators. Moreover, the fuzzy approach provides an opportunity for reservoir operators to develop and apply more convenient operating rules, which in itself is a valuable alternative to conventional optimization techniques.

View PDFchevron_right

References (31)

  1. Bardossy, A, et al. (1990): Fuzzy Regression in Hydrology. Water Resource Research, 26 (7), pp. 1497-1508.
  2. Bellman, Richard (1959): Dynamic Programming, Princeton University Press. New Jersey. Bollmann and Marques (2000): Bases para a Estruturação de Indicadores de Qualidade de Águas. RBRH Vol 5 No.1 Jan/Mar, pp. 37-60. ABRH. Brazil.
  3. Chang, Y.H.O., B.M. Ayyub (2001): Fuzzy regression methods -a comparative assessment. Fuzzy Sets and Systems, 119, pp. 187-203.
  4. Changchit and Terrell (1989): CCGP model for multi-objective reservoir systems. Journal Water Resource Planning and Management, ASCE 115(5), pp. 658-670.
  5. Chaves, P. (2002): Planning Operation of Storage Reservoir for Water Quantity and Quality, Master Thesis, Graduate School of Engineering, Kyoto University, Japan.
  6. Diamond, P. (1988): Fuzzy least square. Information Science, 46, pp. 141-157.
  7. Dombi, J. (1990): Membership function as an evaluation. Fuzzy Sets and Systems, 35, pp. 1-21.
  8. Dubois, D. and Prade, H. (1980): Fuzzy Sets and Systems: Theory and Applications, pp. 393, Academic, California.
  9. El-Swaify and Yakowitz, editors (1998): Multiple Objective Decision Making for Land, Water, and Environment Management, Proceedings of the First International Conference on Multiple Objective Decision Support Systems (MODSS) for Land, Water and Environment Management. CRC Press LLC. Hawaii.
  10. Esogbue, Augustine O., et al. (1989): Dynamic Programming for Optimal Water Resources Systems Analysis. Prentice Hall Inc. USA.
  11. Fontane, D., et al. (1997): Planning Reservoir Operation with Imprecise Objectives, Journal of Water Resources Planning and Management, pp. 154-162, May/June.
  12. Galvao, C. O. and Valenca, M.S. editors (1999): Sistemas Inteligentes: Aplicacoes a Recursos Hidricos e Ciencias Ambientais, ABRH. Brazil.
  13. Hagan et al. (1995): Neural Network Design, PWS Publishing Company, Boston.
  14. Kacprzyk, Janusz (1997): Multistage Fuzzy Control, Wiley. England.
  15. Klir, G. and Yuan, B. (1995): Fuzzy sets and fuzzy logic: theory and applications, Prentice-Hall, Inc., Englewood Cliffs. USA.
  16. Kojiri, Toshiharu (1992): Planning of reservoir Construction through Fuzzy Optimization, DPRI, Japan.
  17. Labadie, J.W. (1993): Combining Simulation and Optimization in River Basin Management, Stochastic Hydrology and its Use in Water Resources Systems Simulation and Optimization, pp. 345-371. NATO ASI Series. Kluwer Academic Publishers. The Netherlands.
  18. Maier, H. and Dandy, G. (2000): Neural networks for the prediction and forecasting of water resources: a review of modeling issues and applications, Environment Modeling & Software, Vol. 15, pp. 101-124.
  19. Norwick, A. and Turksen, I. (1984): A model for the measurement of membership and consequences of its empirical implementation, Fuzzy Sets and Systems, 12(1), pp.1-25.
  20. Porto, Rubem, et al. (2000): Integration of Water Quantity and Quality in Strategic River Basin Planning, Journal of Water Resources Planning and Management, pp. 85-97, March/April. USA.
  21. Rea, L. and Parker, R. (1993): Designing and conducting survey research: a comprehensive guide, Jossey-Bass Pub., San Francisco, CA.
  22. Redden, D.T., Woodall, W.H. (1996): Further examination of fuzzy linear regression. Fuzzy Sets and Systems, 79, pp. 203-211.
  23. Russel, Samuel and Campbell, Paul (1996): Reservoir Operation Rules With Fuzzy Programming, Journal of Water Resources Planning and Management, pp. 165-170.
  24. Savic, D.A., Pedrycz, W. (1991): Evaluation of fuzzy linear regression models, Fuzzy Sets and Systems, 39, pp. 51-63.
  25. Shrestha, Bijaya (1996): Fuzzy Rule-Based Modeling of Reservoir Operation, Journal of Water Resources Planning and Management, pp. 262-269.
  26. Simonovic, S (1991): Coping with changing objectives in managing an existing multipurpose reservoir, Hydro. Of Natural and Manmade Lakes, Publ. No. 206, G. Schiller et al., eds., Int. Assn. of Hydro. Sci., Wallingford, UK, pp. 181-189.
  27. Torabi, M. and Mobasheri, F. (1973): A Stopchastic Dynamic Programming Model for the Optimum Operation of a Multi-purpose Reservoir, Water Resources Bulletin, American Water Resources Association, Vol. 9, No. 6.
  28. Tran, L., L. Duckstein (2002): Multi-objective fuzzy regression with central tendency and possibilistic properties, Fuzzy Sets and Systems, 130, pp. 21-31.
  29. Tundisi, J.G. and Tundisi, M. (1990): Limnology and eutrophication of Barra Bonita Reservoir, S. Paulo State, Southern Brazil. Arch. Hydrobiol. Beith. Ergebn. Limnology, pp. 661-676. Stuttgart.
  30. Yakowitz, Sidney (1982): Dynamic Programming Applications in Water Resource, Water Resources Research, Vol. 18, No. 4, pp. 673-696.
  31. Zalewski, M. et al. (1997): Ecohydrology: A New Paradigma for Sustainable Use of Aquatic Resources, UNESCO. Paris, France.

Related papers

Operation of storage reservoir for water quality by using optimization and artificial intelligence techniques
mayank mukund

Mathematics and Computers in Simulation, 2004

Water quantity and quality are considered to be the main driving forces of the reservoir operation. Barra Bonita reservoir, located in the southeast region of Brazil, is chosen as the case study for the application of the proposed methodology. Herein, optimization and artificial intelligence (AI) techniques are applied in the simulation and operation of the reservoir. A fuzzy stochastic dynamic programming model (FSDP) is developed for calculating the optimal operation procedures. Optimization is applied to achieve multiple fuzzy objectives. Markov chain technique is applied to handle the stochastic characteristics of river flow. Water quality analysis is carried out using an artificial neural network model. Organic matter and nutrient loads are modeled as a function of river discharge through the application of a fuzzy regression model based on fuzzy performance functions. The obtained results show that the proposed methodology provides an effective and useful tool for reservoir operation.

View PDFchevron_right
Deriving reservoir operational strategies considering water quantity and quality objectives by stochastic fuzzy neural networks
Paulo Chaves

Advances in Water Resources, 2007

By taking advantage of the close relationship between quality and quantity of water, we investigated the potential improvements of the in-reservoir water quality through the optimization of reservoir operational strategies. However, the few available techniques for optimization of reservoir operational strategies present some limitations, such as restrictions on the number of state/decision variables, the impossibility considering stochastic characteristics and difficulties for considering simulation/prediction models. One technique which presents great potential for overcoming some of these limitations is applied here and investigated for the first time in such complex system. The method, named stochastic fuzzy neural network (SFNN), can be defined as a fuzzy neural network (FNN) model stochastically trained by a genetic algorithm (GA) based model to yield a quasi optimal solution. The term “stochastically trained” refers to the introduction of a new loop within the training process which accounts for the stochastic variable of the system and its probabilities of occurrence. The SFNN was successfully applied to the optimization of the monthly operational strategies considering maximum water utilization and improvements on water quality simultaneous. Results showed the potential improvements on the water quality through means of hydraulic control.

View PDFchevron_right
An integrated fuzzy optimization and simulation method for optimal quality-quantity operation of reservoir-river system
Arash Azari

Water Supply

In this study, a novel optimization-simulation dynamic approach is developed for optimal water operation of reservoir-river systems to improve the water quality and supply the water demands along the river. To this purpose, the WEAP-QUAL2 K linked model is developed to simulate water quality and quantity, which is coupled to a fuzzy multi-objective imperialist competition algorithm (FMOICA) dynamically. The approach's applicability is demonstrated through the case study of the Dez reservoir river in Iran. The simulation and optimization period is six years (October 2019-September 2025). The stochastic models (SARIMA(1,0,1)(1,1,1)) are used to forecast inflow into the Dez dam reservoir for the simulation period. Given that in the verification stage of the QUAL2 K and WEAP models, it can be concluded that the model has high accuracy in simulating the parameters of water quality and quantity. Two scenarios are considered, the first scenario is used for dynamical coupling of the qua...

View PDFchevron_right
Comparison of stochastic and fuzzy dynamic programming models for the operation of a multipurpose reservoir
Umamahesh Nanduri

Water and Environment Journal

Reservoir management is a highly complex problem, which includes the uncertainty in the inflows as well as in the objectives. Stochastic dynamic programming (SDP) has been widely used to develop the optimal operating policies of multipurpose reservoirs. In the recent years, fuzzy optimization has been used to incorporate the uncertainty caused due to the imprecise nature of objectives. In the present study, a comparison is made between a conventional SDP model and fuzzy dynamic programming models for optimal operation of a multipurpose reservoir. The two models are developed for Hirakud Reservoir on River Mahanadi in the State of Orissa in India. The performance of the reservoir is evaluated under the operating policies derived from these models through simulation. The results indicate that the fuzzy dynamic programming model performs better in achieving the flood control objective and thus in the overall performan1ce of reservoir.

View PDFchevron_right
OPTIMIZATION OF RESERVOIR OPERATION USING NEURO-FUZZY TECHNIQUES
iaeme iaeme

Water resource engineering is mainly concerned with planning, designing and operation of water resources system. This paper explores the use of soft computing tools for water availability and operation studies, deciding suitable advanced optimization techniques for understanding a real life study related to water resources engineering and extension of these techniques to reservoir operation studies

View PDFchevron_right

Related topics

  • Computer Science
  • Petroleum Engineering
    • 580 California St., Suite 400
    San Francisco, CA, 94104
    © 2025 Academia. All rights reserved