CN112526458B - Broadband NLFM (non-line-of-sight) emission beam forming method based on parameter fraction time delay extraction - Google Patents

Abstract

The invention discloses a broadband NLFM (non line frequency modulation) transmitting beam forming method based on extraction parameter fractional time delay, belonging to the technical field of array signal processing. Due to the problem of aperture transit, beam forming of broadband signals requires time delay processing, and a traditional time delay method uses a filter in a time domain and performs DFT in a frequency domain. Most studies on the generation of wideband transmit beams are directed to LFM signals, while few studies are directed to NLFM signals with more complex signal characteristics and excellent pulse pressure performance. The invention provides a broadband NLFM fractional beam forming method, which emphasizes the generation of a digital fractional time delay waveform: dividing the time delay into integer time delay and fractional time delay, obtaining a time domain expression of the broadband NLFM signal by utilizing exponential polynomial fitting processing, directly generating a fractional time delay waveform in a DDS (direct digital synthesizer) by a parameter extraction method, and finally forming a broadband NLFM transmitting beam through the integer time delay.

Description

A Broadband NLFM Transmit Beamforming Method Based on Fractional Delay Extraction Parameters

technical field

The invention belongs to the technical field of array signal processing, and in particular relates to a broadband NLFM transmit beamforming method based on fractional time delay extraction parameters.

Background technique

The commonly used broadband radar signal is LFM signal at present. In pulse compression system radar, LFM signal pulse compression results in higher sidelobes. In order to reduce the side lobe, window function weighting is usually used, which will cause the loss of signal-to-noise ratio and the broadening of the main lobe. However, the NLFM signal has lower range sidelobe after pulse compression, and no weighting is needed, which avoids the loss of signal-to-noise ratio caused by mismatch. Wideband radar systems using NLFM signals have the advantages of both wideband and NLFM signals: low intercept and low pulse compression sidelobes. In wideband array signals, TTD waveform generation is a basic requirement for transmit beamforming. The TTD line can divide the time delay into integer time delay and fractional time delay. In order to realize the fractional time delay of broadband waveform, two digital methods can be used. One is the time-domain approach, where digital variable fractional delay (VFD) filters (such as Farrow structure filters) and others using Newton or spline interpolation have been extensively studied. Another method is the frequency-domain method based on the time-shift characteristics of the Fourier transform, which first transfers the original reference waveform to the frequency domain through the discrete Fourier transform (DFT), and then performs a linear phase shift on each frequency-domain component , and finally the frequency domain components are transferred back to the time domain sequence using inverse DFT (IDFT). However, in the time-domain method, the VFD filter needs hundreds of taps, and the filter is required to have the characteristics of wide bandwidth, high amplitude flatness, and high delay accuracy. For the frequency domain method, in order to meet the delay accuracy, for large time-bandwidth product waveforms, the number of DFT points should not be less than the number of sampling points, and the number of sampling points can exceed 10,000. Although these two methods can effectively achieve arbitrary delay, the hardware and software for implementation are very complex and will consume a lot of resources.

The TTD line can divide the delay into integer delay and fractional delay, and the fractional delay is essentially changing the signal phase and envelope movement. The literature proposes a method of compensating the signal phase in DDS by changing the signal parameters. By analyzing the signal time domain expression, the phase compensation is realized by using the control parameters of the direct digital synthesizer (DDS). But this method needs to obtain the time domain phase expression of the signal. The commonly used NLFM signal is designed through the window function, and its phase expression in the time domain needs to be obtained by inverting and integrating the group delay function, which is implicit. The traditional method of NLFM signal generation is to use the window function and design the waveform through the phase-stationary principle. The current research on NLFM signals is usually to improve the signal generation method, especially the fitting method, in the narrowband background, using polynomials to fit the time domain expression of the NLFM signal or using Fourier series expansion to obtain the signal phase expression . However, trigonometric functions will appear in the expression after Fourier series fitting. If a digital signal processing structure is used to generate a fractional time-delay signal, a large amount of precious multiplier resources will be consumed, while polynomial fitting can use the phase accumulator as much as possible. , less resource consumption.

Contents of the invention

The technical problem to be solved by the present invention is: the system complexity is high in broadband beam forming, and the resource consumption is large. The present invention aims to perform broadband beam forming in a way that consumes less resources.

The present invention adopts the following technical solutions for solving the above-mentioned technical problems: the present invention uses the least squares method to carry out fitting and approximation to the implicit formula, obtains the exponential polynomial expression of the approximate S-type NLFM signal time-domain phase, and then adopts the method of extracting parameters The method directly generates digital fractional delay waveforms. Theoretical derivation results show that using this method can make the fractional delay waveforms emitted by each array element consistent, and the fractional delay waveforms of all array elements can be directly generated only by changing the polynomial parameters. A broadband NLFM transmit beamforming method based on extracting parameter fractional time delays, comprising the following steps:

和波形函数s(t)；Step 1. Select the Hamming window as the signal power spectrum to generate the nonlinear FM signal waveform, and obtain the group delay function and frequency spectrum of the signal according to the phase stationary principle, and the phase function of the signal

and the waveform function s(t);

Step 2. In the TTD-based general uniform linear array transmit beamforming structure, M identical omnidirectional antenna elements radiate delayed waves to divide transmit beam time delay into integer time delay and fractional time delay;

Step 3. Delay the reference array element waveform s ₀ (t) by a corresponding integer multiple of the sampling period, and then generate a fractional time delay waveform according to the fractional time delay F _m of the m array element, so as to realize the signal delay of different array elements;

Step 3-1, obtain the phase of the reference array element signal through the phase polynomial function of the signal;

Step 3-2. Obtain the delay waveform of the m+1th array element according to the waveform of the reference array element, 0<m<M-1;

Step 3-3, calculating the envelope delay and phase shift;

Step 3-4, obtaining the fractional delay waveform of the m+1th array element according to the envelope delay and phase shift;

Step 4. Calculate the input parameters of the general digital signal processing structure based on the phase accumulator and the CORDIC RM module; generate the fractional delay waveform of the broadband NLFM signal according to the input parameters, and then carry out integer delay to form a complete broadband NLFM transmission beam.

Further, the signal amplitude spectrum |S(f)| of the Hamming window in the step 1 satisfies:

Where f is the signal frequency, B is the FM bandwidth; the group delay function T(f) and frequency spectrum f(t) of the signal are:

f(t)=T ^-1 (f)

和波形函数s(t)为：where K ₁ is a constant coefficient; the phase function of the signal

and the waveform function s(t) is:

0≤t≤T

Among them, T is the pulse width of the modulation waveform, and a(t) is the envelope.

Further, in the step 2, the time delay division of the transmit beam under the uniform linear array model is carried out, and the specific process is as follows:

Let the first array element be the reference array element, and the propagation path difference between the m array element and the reference array element results in a time difference τ _tm :

Where θ _t is the angle of arrival, c is the speed of light, d is the distance between array elements, and M is the number of array elements;

In the far field, the instantaneous linear combination of the transmitted signals s _m (t-τ _tm ) delayed by M array elements is the composite signal x(t):

Where s _m (t) is the transmitted signal before the delay of the m+1th array element, 0<m<M-1; δ(t-τ _tm ) is the impulse function of the s _m (t-τ _tm ) function ; δδ(t-τ _m -τ _tm ) is the convolution function of δ(t-τ _m ) and δ(t-τ _tm ), and τ _m is the relative value of the m+1th array element to the reference array when the signal is transmitting The real delay of the element;

According to the sampling period T _s , the real time delay τ _m is divided into integer time delay T _m and fractional time delay F _m as follows:

Wherein Int _m is the number of integer delays, and Round(·) means rounding to the nearest integer.

Further, in the step 3, the generation of the digital fractional delay waveform of the extracted parameters, the specific process is:

The waveform s ₀ (t) of the reference array element is:

为参考阵元信号的相位；设拟合为指数多项式，拟合阶数为n，得参考阵元信号的相位

为：where a ₀ (t) is the envelope of the reference element signal,

is the phase of the reference array element signal; if the fitting is an exponential polynomial, the fitting order is n, and the phase of the reference array element signal is obtained

for:

Among them, P _{i, 0} is obtained according to f(t) discrete value numerical integration and curve fitting, i=0, 1, 2, ..., n-1, n, subscript i represents the parameter corresponding to index i; then the mth The delay waveform s _m (t) of +1 array element is:

为相移，δ(t-T_m)为冲激函数；where a ₀ (tF _m ) is the envelope delay,

is the phase shift, δ(tT _m ) is the impulse function;

Among them, the phase parameter P _i,m of the fractional delay waveform emitted by the m+1th array element is:

为排列组合；第m+1阵元的分数时延波形为：in

It is permutation and combination; the fractional delay waveform of the m+1th array element is:

where A is the constant envelope.

Further, the step 4 calculates the input parameters of the general digital signal processing structure based on the phase accumulator and the CORDIC RM module, and the specific process is:

The G-phase digital signal processing structure is adopted, and the digital sampling clock at this time is:

Where T _CLK is the clock pulse, G is the phase number of the digital signal processing structure; the sampling sequence number under the clock T _s is n _t :

n _t =G i _t +g

i _t = 0, 1, 2, ..., N _G -1, N _G = it /G, g = 0, 1, 2, ..., G- ₁

Where it is the single-phase sampling sequence in the _polyphase structure, N _G is the length of the single-phase sampling sequence, and g is the number of each phase;

Then for the reference array element, the output phase expression of the g+1th phase accumulator structure is:

为第g+1相经过n个相位累加器的结果；

is the result of the g+1th phase passing through n phase accumulators;

Among them, R _{i, 0, g} are the coefficients of each item of the formula, i=1, 2, 3, ..., n-1, n, the subscript i represents the number of accumulators passed, and 0 represents the current corresponding 0 array element , is the reference array element, and g represents the g+1th item in the multiphase structure;

The expression of the discrete phase function of the m+1th array element is:

In the formula, the coefficients are R _{i, m, g} , i=1, 2, 3, ..., n-1, n, the subscript i represents the number of accumulators passed, and m represents the number of the current array element; multi-phase In the digital signal processing structure, the input parameters of the g+1th phase are:

Among them, RW _{m, g} , FW _{i, m, g} , and PW _{m, g} are input parameters of the digital signal processing structure.

Beneficial effects: Compared with the prior art, the technical solution of the present invention has the following beneficial technical effects:

The broadband NLFM transmission beamforming method based on the extraction parameter fractional time delay described in the present invention has a reliable design principle and a simple structure. Compared with the waveform generation of the broadband LFM signal, the method only needs to add a phase accumulator to form a broadband NLFM transmission waveform , while avoiding consumption of multiplier resources, the performance of transmitting signals is improved.

Description of drawings

Fig. 1 is method flowchart of the present invention;

Fig. 2 is a digital signal processing polyphase structure diagram using phase accumulation;

Figure 3 is a diagram of pulse pressure results under different fitting orders;

Figure 4(a) is the four-phase output waveform diagram of the reference array element for FPGA simulation test;

Figure 4(b) is the four-phase output waveform diagram of the reference array element tested by MATLAB simulation;

Fig. 5 (a) is the four-phase output waveform diagram of the second array element of the FPGA simulation test;

Figure 5(b) is the four-phase output waveform diagram of the second array element tested by MATLAB simulation;

FIG. 6 is a beamforming diagram after combining discrete time points in the time domain;

Figure 7 is a comparison chart of pulse pressure of LFM and NLFM echo signals under the same parameters.

Detailed ways

The technical solution of the present invention will be further described in detail below in conjunction with the accompanying drawings.

A kind of broadband NLFM transmission beamforming method based on extraction parameter fractional time delay that the present invention proposes, as shown in Figure 1, specific implementation steps are as follows:

和波形函数s(t)。汉明窗的信号幅度谱|S(f)|满足：Step 1. In order to suppress the distance sidelobe of the output waveform, the Hamming window is selected as the signal power spectrum to generate a nonlinear FM signal waveform, and the group delay function and spectrum of the signal are obtained according to the phase stationary principle, and the phase function of the signal

and the waveform function s(t). The signal magnitude spectrum |S(f)| of the Hamming window satisfies:

Where f is the signal frequency, B is the FM bandwidth; the group delay function T(f) and frequency spectrum f(t) of the signal are:

f(t)=T ^-1 (f)

和波形函数s(t)为：where K ₁ is a constant coefficient; the phase function of the signal

and the waveform function s(t) is:

0≤t≤T

Among them, T is the pulse width of the modulation waveform, and a(t) is the envelope.

Step 2. In the TTD-based general uniform linear array transmit beamforming structure, M identical omnidirectional antenna elements radiate delayed waves to divide transmit beam time delay into integer time delay and fractional time delay;

Carry out the transmit beam delay division under the uniform linear array model, the specific process is as follows:

The propagation path difference between the m array element and the reference array element (the first array element is 0 array element) results in a time difference τ _tm :

Where θ _t is the angle of arrival, c is the speed of light, d is the distance between array elements, and M is the number of array elements;

In the far field, the instantaneous linear combination of the transmitted signals s _m (t-τ _tm ) delayed by M array elements is the composite signal x(t):

Where s _m (t) is the transmitted signal before the delay of the m+1th array element, 0<m<M-1; δ(t-τ _tm ) is the impulse function of the s _m (t-τ _tm ) function ; δ(t-τ _m -τ _tm ) is the convolution function of δ(t-τ _m ) and δ(t-τ _tm ), and τ _m is the ratio of the m+1th array element to the reference array when the signal is transmitting The real time delay of the element; if the maximum power of signal transmission points to the target angle θ _t , then τ _m =-τ _tm ;

According to the sampling period T _s , the real time delay τ _m is divided into integer time delay T _m and fractional time delay F _m as follows:

Wherein Int _m is the number of integer delays, and Round(·) means rounding to the nearest integer.

Step 3. Delay the reference array element waveform s ₀ (t) by a corresponding integer multiple of the sampling period, and then generate a fractional time delay waveform according to the fractional time delay F _m of the m array element, so as to realize the signal delay of different array elements;

Step 3-1, obtain the phase of the reference array element signal through the phase polynomial function of the signal;

Step 3-2. Obtain the delay waveform of the m+1th array element according to the waveform of the reference array element, 0<m<M-1;

Step 3-3, calculating the envelope delay and phase shift;

Step 3-4: Obtain the fractional delay waveform of the m+1th array element according to the envelope delay and phase shift.

The generation of the digital fractional delay waveform of the extracted parameters, the specific process is:

The waveform s ₀ (t) of the reference array element is:

为参考阵元信号的相位；设拟合为指数多项式，拟合阶数为n，得参考阵元信号的相位

为：where a ₀ (t) is the envelope of the reference element signal,

is the phase of the reference array element signal; if the fitting is an exponential polynomial, the fitting order is n, and the phase of the reference array element signal is obtained

for:

Among them, P _{i, 0} is obtained according to f(t) discrete value numerical integration and curve fitting, i=0, 1, 2, ..., n-1, n, subscript i represents the parameter corresponding to index i; then the mth The delay waveform s _m (t) of +1 array element is:

为相移，δ(t-T_m)为冲激函数；where a ₀ (tF _m ) is the envelope delay,

is the phase shift, δ(tT _m ) is the impulse function;

本实施例为S型NLFM信号的包络a(t)＝A，为恒模函数。To realize the signal time delay of different array elements, the reference array element waveform s ₀ (t) can be delayed by the corresponding integer multiple of the sampling period, and then the fractional time delay waveform can be generated according to the fractional time delay F _m . Achieving fractional delay requires calculation of envelope delay a ₀ (tF _m ) and phase shift

In this embodiment, the envelope a(t)=A of the S-type NLFM signal is a constant modulus function.

If different array element signals are synthesized in the same phase in the θ _t direction, the phase parameter of the fractional delay waveform transmitted by the m+1th array element should be P _{i, m} (i=0, 1, 2, ..., n -1, n, the subscript i represents the index corresponding to the parameter i, and m represents the array element number). According to the properties of polynomials, the value of P _{i, m} is known as:

为排列组合，若设定参考阵元的相位拟合多项式参数，则其他M-1个阵元的相位拟合多项式参数P_i，m便全部计算出，得到所有阵元的相位。in

For permutation and combination, if the phase fitting polynomial parameters of the reference array element are set, then the phase fitting polynomial parameters P _{i, m} of the other M-1 array elements are all calculated, and the phases of all array elements are obtained.

The fractional delay waveform of the m+1th array element is:

where A is the constant envelope.

Step 4. Calculate the input parameters of the general digital signal processing structure based on the phase accumulator and the CORDIC RM module; generate the fractional delay waveform of the broadband NLFM signal according to the input parameters, and then carry out integer delay to form a complete broadband NLFM transmission beam. The specific process of calculating the input parameters is as follows:

The G-phase digital signal processing structure is adopted, and the digital sampling clock at this time is:

Where T _CLK is the clock pulse, G is the phase number of the digital signal processing structure; the sampling sequence number under the clock T _s is n _t :

n _t =G i _t +g

i _t = 0, 1, 2, ..., N _G -1, N _G = it /G, g = 0, 1, 2, ..., G- ₁

Where it is the single-phase sampling sequence in the _polyphase structure, N _G is the length of the single-phase sampling sequence, and g is the number of each phase;

Then for the reference array element, the output phase expression of the g+1th phase accumulator structure is:

为第g+1相经过n个相位累加器的结果；

is the result of the g+1th phase passing through n phase accumulators;

Among them, R _{i, 0, g} are the coefficients of each item of the formula, i=1, 2, 3, ..., n-1, n, the subscript i represents the number of accumulators passed, and 0 represents the current corresponding 0 array element , is the reference array element, and g represents the g+1th item in the multiphase structure;

The expression of the discrete phase function of the m+1th array element is:

In the formula, the coefficients are R _{i, m, g} , i=1, 2, 3, ..., n-1, n, the subscript i represents the number of accumulators passed, and m represents the number of the current array element; multi-phase In the digital signal processing structure, the input parameters of the g+1th phase are:

Among them, RW _{m, g} , FW _{i, m, g} , and PW _{m, g} are input parameters of the digital signal processing structure, as shown in Fig. 2 .

Algorithm and processing method of the present invention have passed verification, obtained satisfactory application effect:

1. Experimental conditions

Taking the NLFM signal with bandwidth B=400MHz, pulse width T=10us, center frequency f _c =200MHz as the input signal, sampling frequency f _s =1600MHz, expected emission direction θ _t is 30°, the number of array elements M is 64, the array The element distance d is λ _c /2, λ _c =c/f _c .

2. Simulation content

Simulation 1: Using the 5th order, 16th order, and 50th order fitting, the signal pulse compression curve is obtained. It can be found that when the 16th order is used for fitting, the sidelobe has reached below -40dB after pulse compression, and as the order increases, the improvement of fitting accuracy is not obvious. Figure 3 shows the pulse pressure results under different fitting orders.

Simulation 2: Using a 4-phase digital signal processing system (G=4), input the calculation parameters into the system to obtain the digital wideband fractional time-delay transmission waveforms of each array element. Taking the 0 and 1 array elements as an example, Fig. 4 and Fig. 5 respectively The four-phase output waveforms of the reference array element and the second array element, a is the FPGA simulation test result, and b is the MATLAB simulation result.

Simulation 3: Using the integer time delay proposed by the present invention to extract parameters to form a fractional time delay waveform method, Fig. 6 is a beamforming diagram after combining discrete time points in the time domain.

Simulation 4: Under the same parameter conditions, the comparison of wideband NLFM signal and LFM signal after echo pulse compression. For comparison, the observation time does not cover the entire duration. Figure 7 shows the pulse pressure comparison of LFM and NLFM echo signals under the same parameters.

3. Simulation result analysis

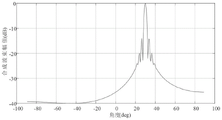
It can be seen from Figure 3 that when the 16-order fitting is used, the sidelobe has reached below -40dB after pulse compression, and the improvement of the fitting accuracy is not obvious as the order increases. It can be seen from Figure 4 and Figure 5 that the FPGA simulation results are consistent with the MATLAB software simulation results, and this method produces accurate fractional delay waveforms. It can be seen from Figure 6 that the beam is accurately pointed to the preset 30°, the combined direction of the transmitted beam is good, and there is no obvious offset distortion. It can be seen from Figure 7 that compared with the LFM signal, the NLFM signal will slightly broaden the main lobe, but the side lobe is significantly reduced, and the reduction is more than 20dB, which is an obvious improvement.

Claims (5)

1. A broadband NLFM transmit beamforming method based on extracting parameter fraction time delay, it is characterized in that, the method comprises the following concrete steps: Step 1. Select the Hamming window as the signal power spectrum to generate the nonlinear FM signal waveform, and obtain the group delay function and frequency spectrum of the signal according to the phase stationary principle, and the phase function of the signal

and the waveform function s(t); Step 2. In the TTD-based general uniform linear array transmit beamforming structure, M identical omnidirectional antenna elements radiate delayed waves to divide transmit beam time delay into integer time delay and fractional time delay; Step 3. Delay the reference array element waveform s ₀ (t) by a corresponding integer multiple of the sampling period, and then generate a fractional time delay waveform according to the fractional time delay F _m of the m array element, so as to realize the signal delay of different array elements; Step 3-1, obtain the phase of the reference array element signal through the phase polynomial function of the signal; Step 3-2. Obtain the delay waveform of the m+1th array element according to the waveform of the reference array element, 0<m<M-1; Step 3-3, calculating the envelope delay and phase shift; Step 3-4, obtaining the fractional delay waveform of the m+1th array element according to the envelope delay and phase shift; Step 4. Calculate the input parameters of the general digital signal processing structure based on the phase accumulator and the CORDIC RM module; generate the fractional delay waveform of the broadband NLFM signal according to the input parameters, and then carry out integer delay to form a complete broadband NLFM transmission beam. 2. the wideband NLFM transmission beamforming method based on extracting parameter fraction time delay according to claim 1, is characterized in that, the signal amplitude spectrum | S (f) | of Hamming window in the described step 1 satisfies:

Where f is the signal frequency, B is the FM bandwidth; the group delay function T(f) and frequency spectrum f(t) of the signal are:

f(t)=T ^-1 (f) where K ₁ is a constant coefficient; the phase function of the signal

and the waveform function s(t) is:

0≤t≤T Among them, T is the pulse width of the modulation waveform, and a(t) is the envelope. 3. the broadband NLFM transmission beamforming method based on extraction parameter fraction time delay according to claim 2, it is characterized in that, described step 2 carries out the transmission beam time delay division under the uniform linear array model, and concrete process is: Let the first array element be the reference array element, and the propagation path difference between the m array element and the reference array element results in a time difference τ _tm :

Where θ _t is the angle of arrival, c is the speed of light, d is the distance between array elements, and M is the number of array elements; In the far field, the instantaneous linear combination of the transmitted signals s _m (t-τ _tm ) delayed by M array elements is the composite signal x(t):

Where s _m (t) is the transmitted signal before the delay of the m+1th array element, 0<m<M-1; δ(t-τ _tm ) is the impulse function of the s _m (t-τ _tm ) function ; v(t-τ _m -τ _tm ) is the convolution function of δ(t-τ _m ) and δ(t-τ _tm ), and τ _m is the relative value of the m+1th array element to the reference array when the signal is transmitting The real delay of the element; According to the sampling period T _s , the real time delay τ _m is divided into integer time delay T _m and fractional time delay F _m as follows:

Wherein Int _m is the number of integer delays, and Round(·) means rounding to the nearest integer. 4. the broadband NLFM transmission beamforming method based on extracting parameter fractional time delay according to claim 3, is characterized in that, in described step 3, the generation of the digital fractional time delay waveform of extracting parameter, concrete process is: The waveform s ₀ (t) of the reference array element is:

where a ₀ (t) is the envelope of the reference element signal,

is the phase of the reference array element signal; if the fitting is an exponential polynomial, the fitting order is n, and the phase of the reference array element signal is obtained

for:

Among them, P _{i, 0} is obtained according to f(t) discrete value numerical integration and curve fitting, i=0, 1, 2, ..., n-1, n, subscript i represents the parameter corresponding to index i; then the mth The delay waveform s _m (t) of +1 array element is:

where a ₀ (tF _m ) is the envelope delay,

is the phase shift, δ(tT _m ) is the impulse function;

Among them, the phase parameter P _i,m of the fractional delay waveform emitted by the m+1th array element is:

in

It is permutation and combination; the fractional delay waveform of the m+1th array element is:

where A is the constant envelope. 5. the broadband NLFM transmission beamforming method based on extracting parameter fraction time delay according to claim 4, is characterized in that, described step 4, calculates the input based on the general digital signal processing structure of phase accumulator and CORDIC RM module parameters, the specific process is: The G-phase digital signal processing structure is adopted, and the digital sampling clock at this time is:

Where T _CLK is the clock pulse, G is the phase number of the digital signal processing structure; the sampling sequence number under the clock T _s is n _t : n _t =G i _t +g i _t = 0, 1, 2, ..., N _G -1, N _G = it /G, g = 0, 1, 2, ..., G- ₁ Where it is the single-phase sampling sequence in the _polyphase structure, N _G is the length of the single-phase sampling sequence, and g is the number of each phase; Then for the reference array element, the output phase expression of the g+1th phase accumulator structure is:

is the result of the g+1th phase passing through n phase accumulators; Among them, R _{i, 0, g} are the coefficients of each item of the formula, i=1, 2, 3, ..., n-1, n, the subscript i represents the number of accumulators passed, and 0 represents the current corresponding 0 array element , is the reference array element, and g represents the g+1th item in the multiphase structure; The expression of the discrete phase function of the m+1th array element is:

In the formula, the coefficients are R _{i, m, g} , i=1, 2, 3, ..., n-1, n, the subscript i represents the number of accumulators passed, and m represents the number of the current array element; multi-phase In the digital signal processing structure, the input parameters of the g+1th phase are:

Among them, RW _{m, g} , FW _{i, m, g} , and PW _{m, g} are input parameters of the digital signal processing structure.

Images