Figure 6 – uploaded by Ghada Afifi
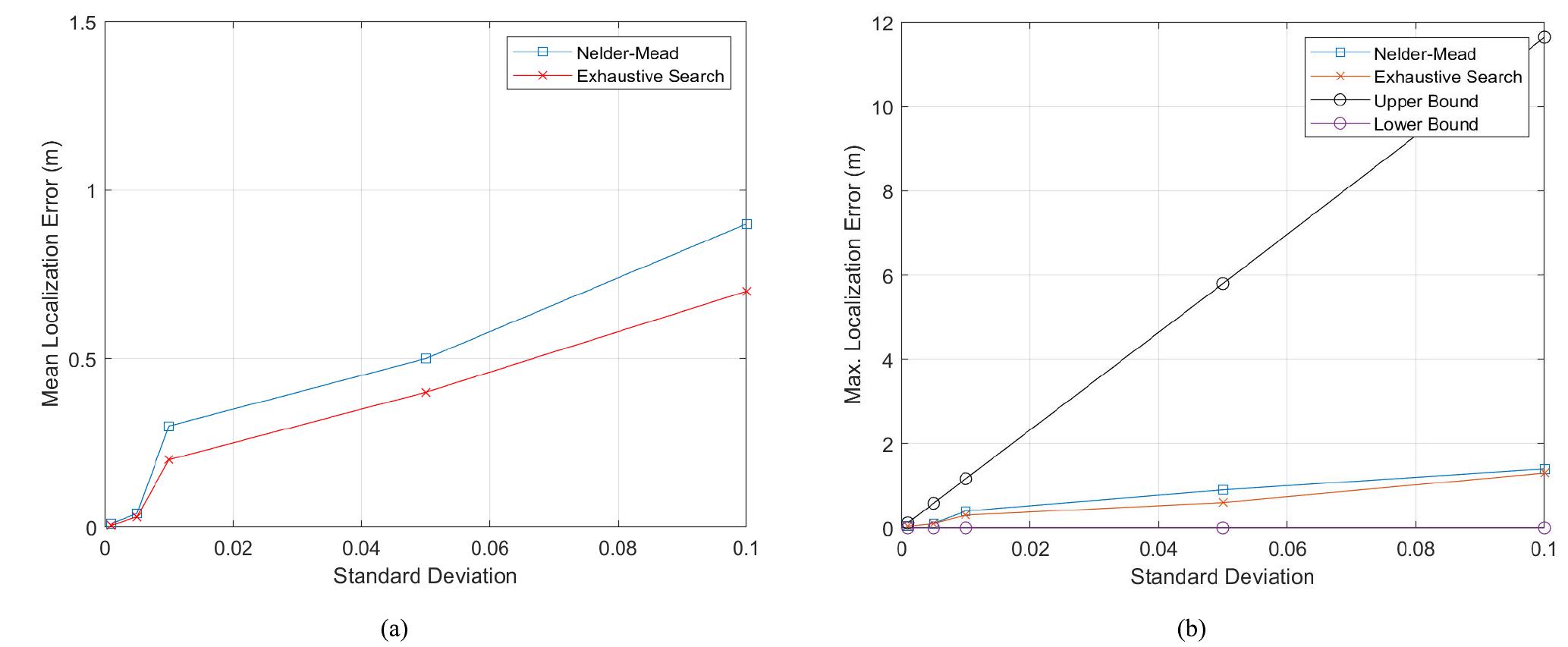
Figure 5 Optimization-based localization results (a) Mean localization error for exhaustive search vs. Nelder-Mead; (b) Maximum localization error as compared to theoretical bounds for exhaustive search vs. Nelder-Mead. and v;(k) is the zero mean gaussian measurement noise. The carrier phase observable can be re-parametrized in terms of UAV and BS positions as follows The above estimation ignores the initial measurement noise. However, the authors propose to average several mea- surements for the total duration in which the GPS is initially available. To estimate the common bias term cét (k), the authors propose to lump the N BS; clocks into clusters, each of size Nj where N = iy N_ and L is the total number of clusters. Extending this approach to our application scenario to localize the UAV through measurements from four base stations, we let N = 4 and L < 2. Note that, given the 2-D position of the UAV is being estimated with L clock clus- ters, the number of clusters, L, cannot exceed N-2. Next, the authors utilize a weighted non-linear least squares (WNLS) estimator to estimate the UAV location given by









