580 California St., Suite 400
San Francisco, CA, 94104
Figure 8 – uploaded by Reinhard Koenig
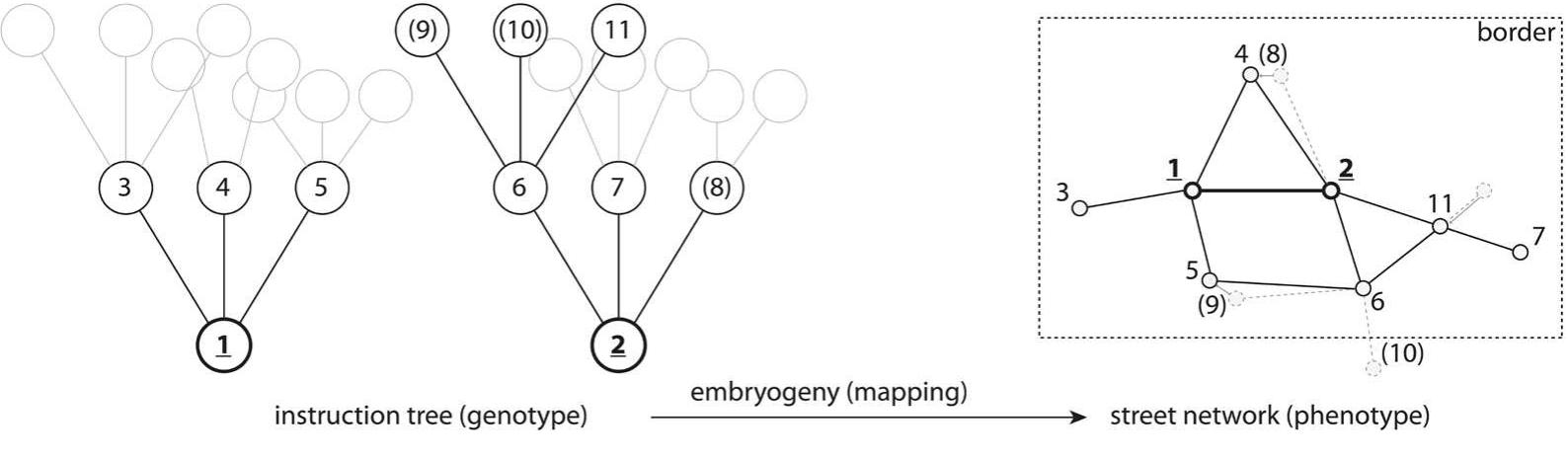
Figure 6 left-hand network in Figure 6 we find that there is no single bottleneck, and at least one other populated route. As a result this network has the worst fitness of the three. the diagrams in the bottom row in Figure 7 is similar to that of the corresponding diagrams in Figure 6. This indicates that both fitness functions direct the search process in a similarly efficient way. Our third example is based on the initial sce- nario with two defined sub-areas as shown in the right-hand image of Figure 5. In Figure 8 the central sub-area is shown as a dotted ellipse and the quiet sub-area as a dotted rectangle. To include the spatial aspect in the fitness function, we have to define how to represent the graphical objects that represent the sub-areas with the corresponding specified proper- ties. The fact that the three best networks have differ- ent maximal fitness values (diagrams in the bottom row of Figures 6 and 7), indicates that the evolution- ary optimization process explores different parts of the search space each time it is run. But despite the small differences in the maximum fitness values of the variants, they all fulfill the requirements relative- ly well. When we consider the random points (repre- senting randomly generated variants) we can clearly see the advantage of using the evolutionary search process compared to randomly generated solutions. The best variants are improved continuously over the 50 generations and reach a level, which cannot be achieved by a random generation process.
Related Figures (8)
