Academia.eduAcademia.edu

Figure 7 – uploaded by ANTONIO MUÑOZ SUDUPE

See full PDFdownloadDownload figure
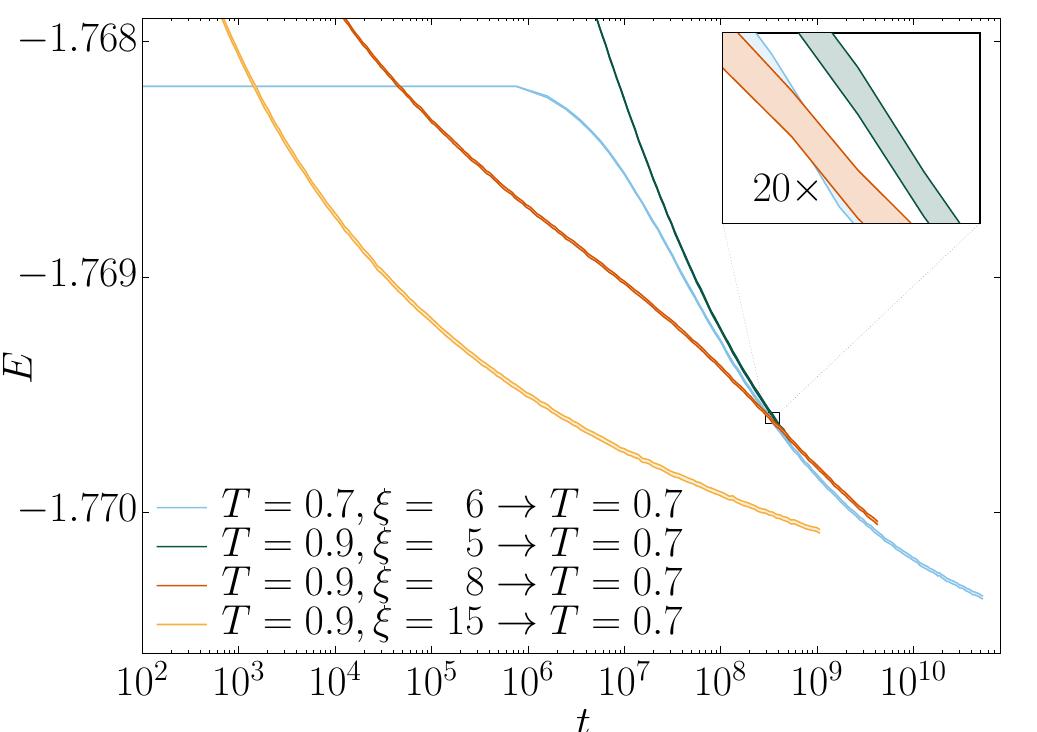
Fig. 7. Improving the accuracy with control variates. The figure shows the ratio of statistical errors, as a function of €(t), for the naive [ Eq. (6)] ane improved [ Eq. (8)] estimates of the energy density. The data shown correspond to three different relaxations. Two of them are isothermal relaxations starting from € = Oatt = O. The third relaxation corresponds to the preparation starting at (T = 0.9, € = 5) which is quenched to T = 0.7 at t = 0 (i.e. the green curves ir Figs. 3 and 4). The error reduction is largest for the isothermal relaxation at T = 0.7 and 219 < t < 2?!) of course (after all, this is the temperature and time region defining the control variate), but the error reduction is also very significant at other times and temperatures.

Figure 7 Improving the accuracy with control variates. The figure shows the ratio of statistical errors, as a function of €(t), for the naive [ Eq. (6)] ane improved [ Eq. (8)] estimates of the energy density. The data shown correspond to three different relaxations. Two of them are isothermal relaxations starting from € = Oatt = O. The third relaxation corresponds to the preparation starting at (T = 0.9, € = 5) which is quenched to T = 0.7 at t = 0 (i.e. the green curves ir Figs. 3 and 4). The error reduction is largest for the isothermal relaxation at T = 0.7 and 219 < t < 2?!) of course (after all, this is the temperature and time region defining the control variate), but the error reduction is also very significant at other times and temperatures.

Related Figures (6)

Fig. 1. Spin-glass coherence length. Top left: A snapshot of a configuration {s& }, which has evolved for t = 28° Monte Carlo steps at T = 0.7 © 0.64Ts. We show the average magnetization on the xy plane, averaging over z. Bottom left: Another configuration {5} of the same sample, prepared in the same way as {8 }. No visible ordering is present in either configuration because the preferred pattern of the magnetic domains cannot be seen by eye (s = 1 is plotted in yellow, and —1in blue). Right: If one measures the overlap between the two configurations, see Eq. (5) in Materials and Methods, and with the same color code used for the spins, the preferred pattern of the magnetic domains, of size €, becomes visible. A reliable method to extract € from the overlap fields has been known for some time (24), but only in 2018 has it been possible to reach accuracies better than 1% in € (25), thanks to the Janus II computer (19) and the use of many clones for the same sample (this strategy works only if the system size, which here is L = 160, turns out to be much larger than &).
Fig. 1. Spin-glass coherence length. Top left: A snapshot of a configuration {s& }, which has evolved for t = 28° Monte Carlo steps at T = 0.7 © 0.64Ts. We show the average magnetization on the xy plane, averaging over z. Bottom left: Another configuration {5} of the same sample, prepared in the same way as {8 }. No visible ordering is present in either configuration because the preferred pattern of the magnetic domains cannot be seen by eye (s = 1 is plotted in yellow, and —1in blue). Right: If one measures the overlap between the two configurations, see Eq. (5) in Materials and Methods, and with the same color code used for the spins, the preferred pattern of the magnetic domains, of size €, becomes visible. A reliable method to extract € from the overlap fields has been known for some time (24), but only in 2018 has it been possible to reach accuracies better than 1% in € (25), thanks to the Janus II computer (19) and the use of many clones for the same sample (this strategy works only if the system size, which here is L = 160, turns out to be much larger than &).
Fig. 2. Classical Mpemba protocol. We show the time evolution of the energy of spin glass systems initially prepared at a higher temperature (T’ = 1.3, red line) or at a lower temperature (T’ = 1.2, blue lines), but always in the paramagnetic (high-temperature) phase (T; ~ 1.10). In all three cases the systems are initially left to evolve out of equilibrium until they reach the internal energies shown in the figure key. At t = O all preparations are quenched, that is, put in contact with a thermal reservoir at temperature T = 0.7 & 0.647%. As discussed in the text, the instantaneous internal energy is a measure of the (off-equilibrium) sample temperature. In agreement with the original Mpemba experiment (1), the system originally at the higher energy cools faster. Bottom left inset: Closeup of the first crossing between energy curves, showing the very small error bars, equal to the thickness of the lines (here and in all other figures, error bars represent one standard deviation; control variates, see (30) and Materials and Methods, are used to improve accuracy). Top right inset: Closeup of the second crossing between energy curves.
Fig. 2. Classical Mpemba protocol. We show the time evolution of the energy of spin glass systems initially prepared at a higher temperature (T’ = 1.3, red line) or at a lower temperature (T’ = 1.2, blue lines), but always in the paramagnetic (high-temperature) phase (T; ~ 1.10). In all three cases the systems are initially left to evolve out of equilibrium until they reach the internal energies shown in the figure key. At t = O all preparations are quenched, that is, put in contact with a thermal reservoir at temperature T = 0.7 & 0.647%. As discussed in the text, the instantaneous internal energy is a measure of the (off-equilibrium) sample temperature. In agreement with the original Mpemba experiment (1), the system originally at the higher energy cools faster. Bottom left inset: Closeup of the first crossing between energy curves, showing the very small error bars, equal to the thickness of the lines (here and in all other figures, error bars represent one standard deviation; control variates, see (30) and Materials and Methods, are used to improve accuracy). Top right inset: Closeup of the second crossing between energy curves.
Fig. 3. Mpemba effect in the spin-glass phase. As in Fig. 2, but all four initial preparations (see text for details) are now carried out in the spin-glass phase (T. < T,). The preparation that cools faster is not the initially coldest one (blue curve), but the one with the largest initial coherence length (yellow curve). The last point in the isothermal relaxation at T’ = 0.7 corresponds with the same time as the configurations shown in Fig. 1. Inset: A zoom of the second crossing point between the curves for preparations (T’ = 0.9, € = 8; red curve) and (T' = 0.7, € = 6; blue curve). This second crossing is not the ME. Rather, the ME arises at the first crossing at t © 5 x 10*. The second crossing disappears if one plots parametrically E(t) as a function of €(t). In other words, the description afforded by Eq. (2) is very accurate, but not exact.
Fig. 3. Mpemba effect in the spin-glass phase. As in Fig. 2, but all four initial preparations (see text for details) are now carried out in the spin-glass phase (T. < T,). The preparation that cools faster is not the initially coldest one (blue curve), but the one with the largest initial coherence length (yellow curve). The last point in the isothermal relaxation at T’ = 0.7 corresponds with the same time as the configurations shown in Fig. 1. Inset: A zoom of the second crossing point between the curves for preparations (T’ = 0.9, € = 8; red curve) and (T' = 0.7, € = 6; blue curve). This second crossing is not the ME. Rather, the ME arises at the first crossing at t © 5 x 10*. The second crossing disappears if one plots parametrically E(t) as a function of €(t). In other words, the description afforded by Eq. (2) is very accurate, but not exact.
Fig. 4. Relationship between the energy density E and the coher- ence length €. As suggested by Eq. (2), for isothermal relaxations (in the plot T = 0.7 and 0.9, depicted with continuous lines) E is an essentially linear function of 1/e?® (at least for the plotted range of € > 4.8). Furthermore, the dependence of the slope on temperature is marginal. Temperature-varying protocols are seen to be essentially vertical moves between the straight lines corresponding to isothermal relaxations at the initial and final temperatures. These vertical moves are very quick initial transients, in which (in moves to higher temperatures only), € slightly decreases and then increases again.
Fig. 4. Relationship between the energy density E and the coher- ence length €. As suggested by Eq. (2), for isothermal relaxations (in the plot T = 0.7 and 0.9, depicted with continuous lines) E is an essentially linear function of 1/e?® (at least for the plotted range of € > 4.8). Furthermore, the dependence of the slope on temperature is marginal. Temperature-varying protocols are seen to be essentially vertical moves between the straight lines corresponding to isothermal relaxations at the initial and final temperatures. These vertical moves are very quick initial transients, in which (in moves to higher temperatures only), € slightly decreases and then increases again.
Fig. 5. A tiny inverse Mpemba effect. Time evolution of the energy, for the three different preparations described in the main text, compared with a quench from T = otoT = 1.4 (top curve). In the three cases, the initial temperature is in the spin glass phase, and the final temperature is T = 1.4 > T.. Avery small ME is found at the time pointed by the arrow, only when warming up samples with similar starting energy.
Fig. 5. A tiny inverse Mpemba effect. Time evolution of the energy, for the three different preparations described in the main text, compared with a quench from T = otoT = 1.4 (top curve). In the three cases, the initial temperature is in the spin glass phase, and the final temperature is T = 1.4 > T.. Avery small ME is found at the time pointed by the arrow, only when warming up samples with similar starting energy.
Fig. 6. Coherence length: Undershooting and convergence to a master curve. Coherence lengths € of the experiments described in Fig. 5. The time evolution of & tends to converge towards the curve corresponding to a quench from T’ = oo to T = 1.4 (bottom curve), giving rise to an undershoot of € when its initial value is higher than the equilibrium € at T = 1.4.
Fig. 6. Coherence length: Undershooting and convergence to a master curve. Coherence lengths € of the experiments described in Fig. 5. The time evolution of & tends to converge towards the curve corresponding to a quench from T’ = oo to T = 1.4 (bottom curve), giving rise to an undershoot of € when its initial value is higher than the equilibrium € at T = 1.4.
Related topics:
MathematicsPhysicsCondensed Matter PhysicsMaterials ScienceMedicineSpin GlassesMemory EffectsSpin GlassMpemba Effect
580 California St., Suite 400
San Francisco, CA, 94104
© 2025 Academia. All rights reserved