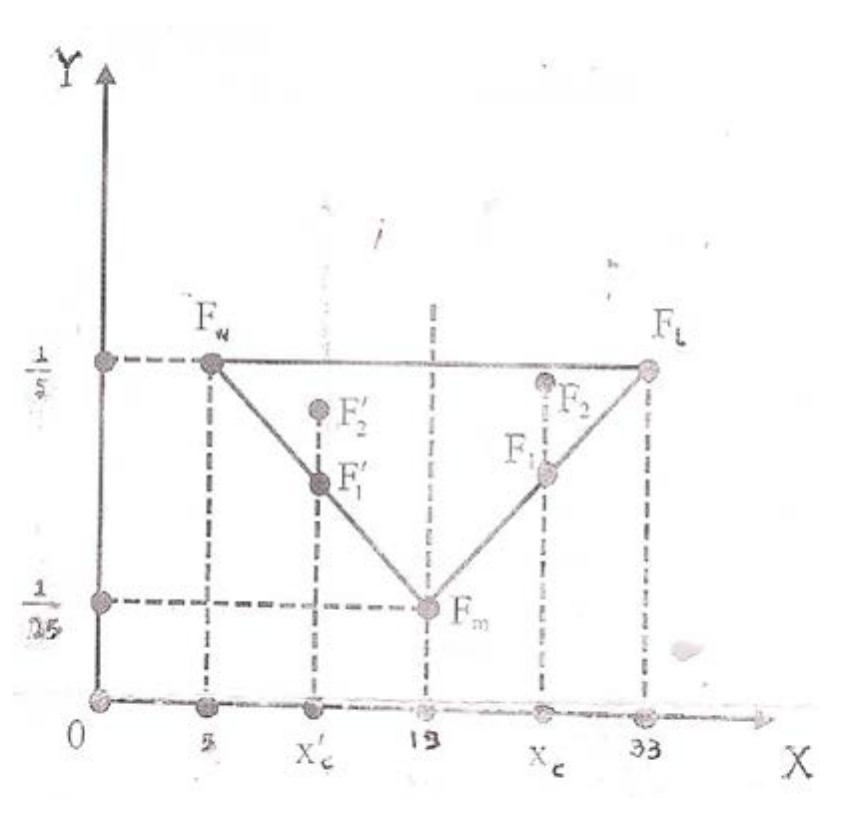
Figure 1 – uploaded by Michael Voskoglou

Figure 1 However, when applying the TFAM, the use of the analytic form of y = m(x) is not needed (in contrast to the case of the classical COG technique) for the calculation of the COG of the resulting level’s area. In fact, since the marginal cases of students’ grades should be considered as common parts for any pair of the adjacent triangles, it is logical to don’t subtract the areas of the intersections from t t t t t he area of the corresponding level’s section, although in his way we count them twice; e.g. placing the ambiguous cases B+ and A- in both regions B and A. In other words, he classical COG technique, which calculates the coordinates of the COG of the area between the graph of he membership function (line OA;B,;A,B.A; B3A, B4As5Cy) and the OX axis (see Figure 1), thus considering he areas of the “common” triangles C,B,C:, C3B2C4, Cs5B3C, and C7B,4Cs only once, is not the proper one to be applied in the above situation. Figure 1. The membership function’s graph of TFAM