580 California St., Suite 400
San Francisco, CA, 94104
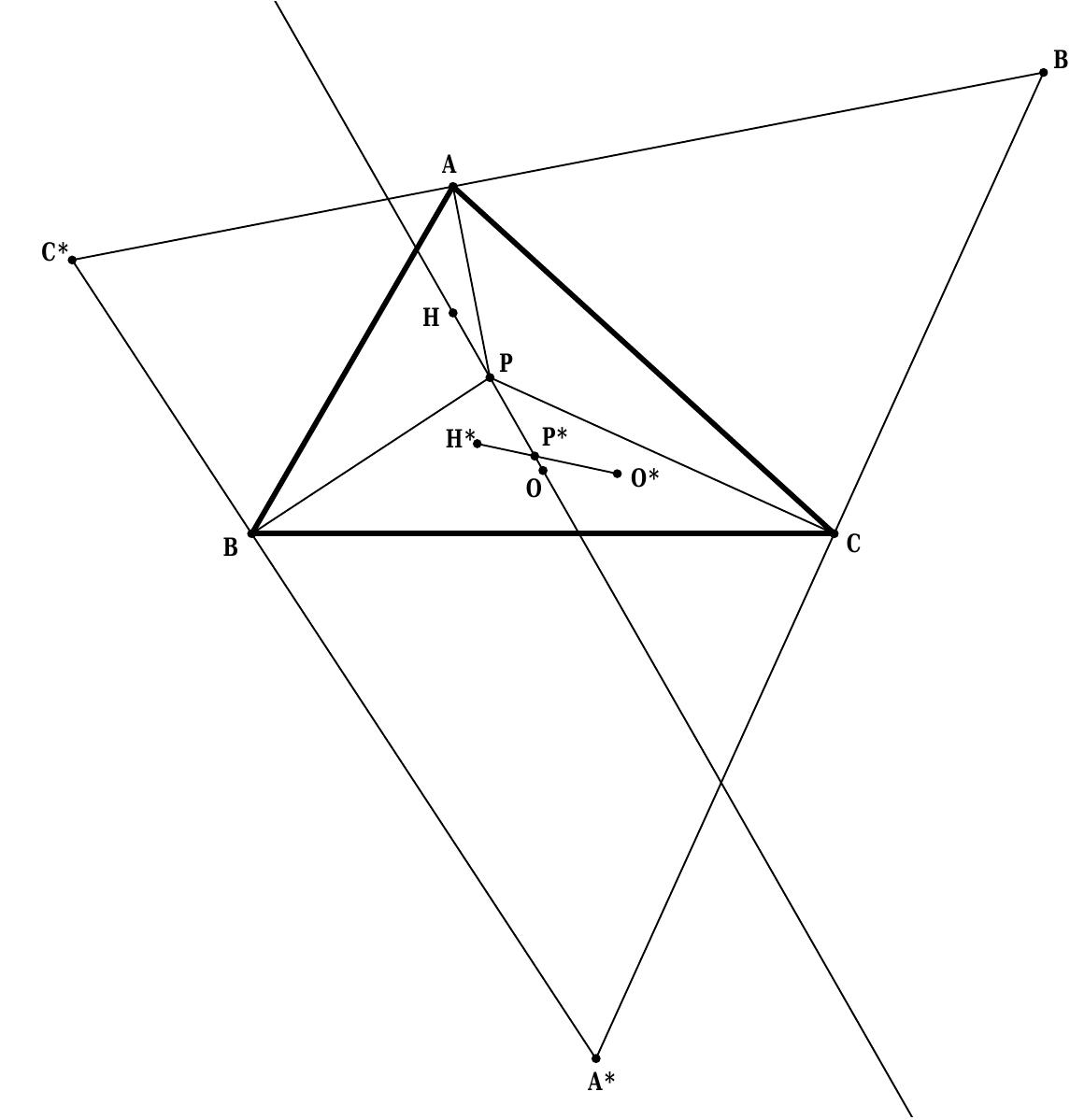
Figure 10 A beautiful sub-case of the Liang-Zelich Theorem. Theorem 3.1. Let P be a point on the Euler line of a triangle ABC. Suppose iy = t (this ratio is directed), where O, H denote the circumcenter and orthocenter of ABC. Let the antipedal triangle of P wrt ABC be A*B*C* and let P* be a point on the Euler line of A* B*C* such that io = t, where O*, H*™ are defined analogously. Then P* is also on the Euler line of ABC.