Heuristic Approaches for Solving N-Queens Problem
2011, Journal of Applied and Emerging Sciences
Sign up for access to the world's latest research
Abstract
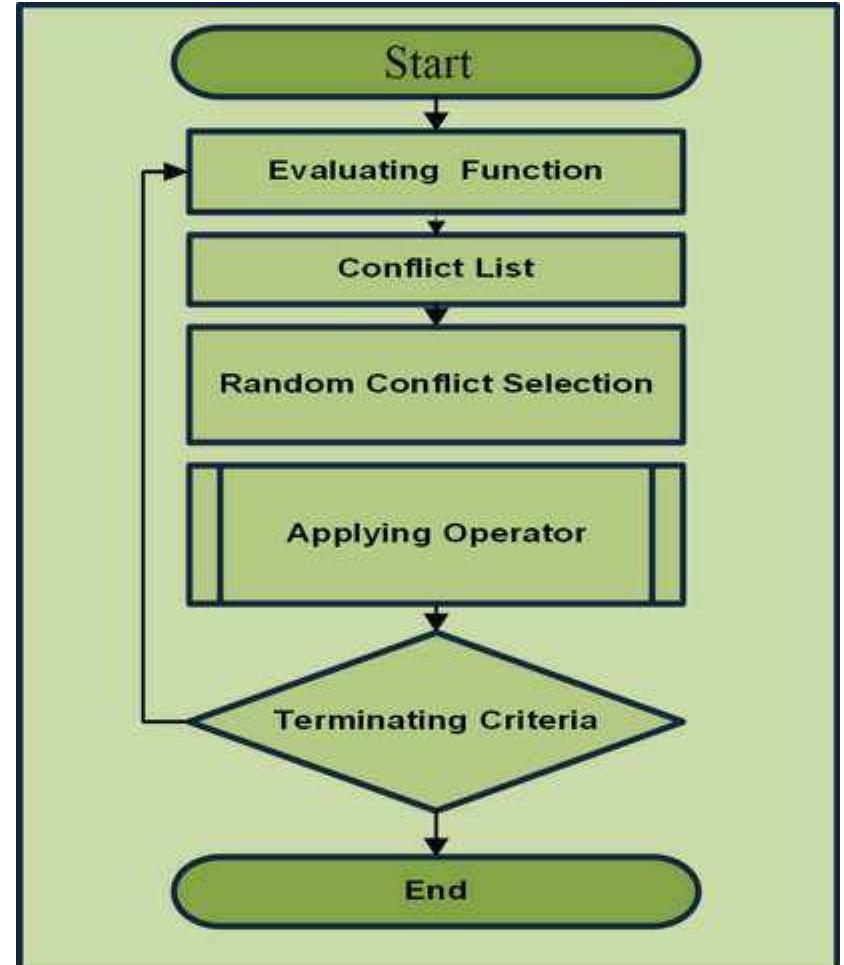
The research article examines the three distinguished heuristics approaches for solving the N-Queens problem. The problem is widely recognized as constraint satisfaction problems (CSP) in the domain of Artificial Intelligence. The N-Queens problem demands the non-attacking placements of finite number of queens over chessboard. So that, two or more queens cannot share the horizontal, vertical and diagonal positions in a straight line. In this research work, improved version of Backtracking Recursive Algorithm, modified Min-Conflicts Algorithm and classic Genetic Algorithm are applied to address the problem. The comparative results validate the efficiency of research direction.
Key takeaways
AI
AI
- The study evaluates three heuristics for the N-Queens problem: Backtracking, Min-Conflicts, and Genetic Algorithms.
- Constraints Logic Programming (CLP) demonstrated high effectiveness in solving the N-Queens problem.
- N-Queens is classified as a Non-deterministic Polynomial-time Hard (NP-hard) problem.
- The research utilized a Lenovo® Intel CORE ™ i3, 2.27 GHz, 2.00 GB RAM for empirical testing.
- Future work aims to compare CLP against Genetic Algorithms, Particle Swarm Optimization, and Simulated Annealing.







Related papers
International Journal in Foundations of Computer Science & Technology
ABSTRACT This Paper provides a brief description of the Genetic Algorithm (GA), the Simulated Annealing (SA) Algorithm, the Backtracking (BT) Algorithm and the Brute Force (BF) Search Algorithm and attempts to explain the way as how our Proposed Genetic Algorithm (GA), Proposed Simulated Annealing (SA) Algorithm using GA, Classical Backtracking (BT) Algorithm and Classical Brute Force (BF) Search Algorithm can be employed in finding the best solution of N Queens Problem and also, makes a comparison between these four algorithms. It is entirely a review based work. The four algorithms were written as well as implemented. From the Results, it was found that, the Proposed Genetic Algorithm (GA) performed better than the Proposed Simulated Annealing (SA) Algorithm using GA, the Backtracking (BT) Algorithm and the Brute Force (BF) Search Algorithm and it also provided better fitness value (solution) than the Proposed Simulated Annealing Algorithm (SA) using GA, the Backtracking (BT) Algorithm and the Brute Force (BF) Search Algorithm, for different N values. Also, it was noticed that, the Proposed GA took more time to provide result than the Proposed SA using GA.
Genetic algorithms are stochastic search techniques that guide a population of solutions towards an optimum using the principles of evolution and natural genetics. This paper shows the way that genetic algorithms can be used to solve 4-Queen problem. The NQP is a classical artificial intelligence problem. The N-Queens problem can be defined as follows: place N queens on an N x N chessboard, each queen on a square, so that no queen could capture any of the others, that is, a configuration in which there exists at most one queen on a given row, column or diagonal. Experimentally results shows that the genetic algorithm have the ability to find optimal solution or find solutions nearby optimal solutions. And The Genetic Algorithm is well suited to has been extensively applied to solve complex design optimization problems because it can handle both discrete and continuous variables, and nonlinear objective and constrain functions without requiring gradient information.
Journal of Optimization
In the field of computing, combinatorics, and related areas, researchers have formulated several techniques for the Minimum Dominating Set of Queens Problem (MDSQP) pertaining to the typical chessboard based puzzles. However, literature shows that limited research has been carried out to solve the MDSQP using bioinspired algorithms. To fill this gap, this paper proposes a simple and effective solution based on genetic algorithms to solve this classical problem. We report results which demonstrate that near optimal solutions have been determined by the GA for different board sizes ranging from 8 × 8 to 11 × 11.
2012
The n-queens problem is a classical combinatorial optimization problem which has been proved to be NPhard. The goal is to place n non-attacking queens on an n×n chessboard. In this paper, the Imperialist Competitive Algorithm (ICA), which is a recent evolutionary metaheuristic method, has been applied for solving the n-queens problem. As another variation, the ICA was combined with a local search method, resulting the Hybrid ICA (HICA). Extensive experimental results showed that the proposed HICA outperformed the basic ICA in terms of average runtimes and average number of fitness function evaluations. The developed algorithms were also compared to the Cooperative PSO (CPSO) algorithm, which is currently the best algorithm in the literature for finding the first valid solution to the n-queens problem, and the results showed that the HICA dominates the CPSO by evaluating the fitness function fewer times.
2015 Science and Information Conference (SAI), 2015
This research proposes the swapping algorithm a new algorithm for solving the n-queens problem, and provides data from experimental performance results of this new algorithm. A summary is also provided of various meta-heuristic approaches which have been used to solve the n-queens problem including neural networks, evolutionary algorithms, genetic programming, and recently Imperialist Competitive Algorithm (ICA). Currently the Cooperative PSO algorithm is the best algorithm in the literature for finding the first valid solution. Also the research looks into the effect of the number of hidden nodes and layers within neural networks and the effect on the time taken to find a solution. This paper proposes a new swapping algorithm which swaps the position of queens.
The N-queens problem is a popular classic puzzle where numbers of queen were to be placed on an n x n matrix such that no queen can attack any other queen. The Branching Factor grows in a roughly linear way, which is an important consideration for the researchers. However, many researchers have cited the issues with help of artificial intelligence search patterns say DFS, BFS and backtracking algorithms. The proposed algorithm is able to compute one unique solution in polynomial time when chess board size is greater than 7. This algorithm is based on 8 different series. For each series a different approach is taken to place the queen on a given chess board.
Rivin, I. and R. Zabih, A dynamic programming solution to the n-queens problem, Information Processing Letters 41 (1992) 253-256.
Proceedings of the 2014 conference companion on Genetic and evolutionary computation companion, 2014
In this paper the influence of using heuristic functions to initialize the population of a classic genetic algorithm (GA) applied to the N-Queens Problem (NQP) is analyzed. The aim of this work is to evaluate the impact of the heuristic initialization phase on the results of the classic GA. In order to probe this, several experiments using two different initialization functions have been carried out. In this paper, the well-known NQP has been used as benchmark problem, but the objective of the authors is to contrast the findings of this study with other combinatorial optimization problems.
Iraqi Journal of Science, 2021
The swarm intelligence and evolutionary methods are commonly utilized by researchers in solving the difficult combinatorial and Non-Deterministic Polynomial (NP) problems. The N-Queen problem can be defined as a combinatorial problem that became intractable for the large ‘n’ values and, thereby, it is placed in the NP class of problems. In the present study, a solution is suggested for the N-Queen problem, on the basis of the Meerkat Clan Algorithm (MCA). The problem of n-Queen can be mainly defined as one of the generalized 8-Queen problem forms, for which the aim is placing 8 queens in a way that none of the queens has the ability of killing the others with the use of the standard moves of the chess queen. The Meerkat Clan environment is a directed graph, called the search space, produced for the efficient search of valid n-queens’ placement, in a way that they do not cause harm to one another. This paper also presents the development of an intelligent heuristic function which is ...
Abstract: Most of the optimization methods do not inherit convergence proofs. One of the measures to rank them is their potential to solve challenging problems specially formulated for this purpose. In this paper the problem involves two main issues. Firstly we present new formulations of the N queens’ configuration problem as optimization problems and secondly we modify a derivative free method so that it may be able to find the optimal configuration of the chessboard.

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
 Mazhar Ali
Mazhar Ali