Academia.eduAcademia.edu

Outline

Title
Abstract
Key Takeaways
Figures
Introduction
Conclusion
References
All Topics
Computer Science
Theoretical Computer Science

HODLR2D: A new class of Hierarchical matrices

Profile image of Vaishnavi GujjulaVaishnavi Gujjula

2022, ArXiv

https://doi.org/10.48550/ARXIV.2204.05536
visibility

…

description

26 pages

link

1 file

Abstract

This article introduces HODLR2D, a new hierarchical low-rank representation for a class of dense matrices arising out of N body problems in two dimensions. Using this new hierarchical framework, we propose a new fast matrix-vector product that scales almost linearly. We apply this fast matrix-vector product to accelerate the iterative solution of large dense linear systems arising out of radial basis function interpolation and discretized integral equation. The space and computational complexity of HODLR2D matrix-vector products scales as O(pN log(N)), where p is the maximum rank of the compressed matrix subblocks. We prove that p ∈ O (log (N) log (log (N))), which ensures that the storage and computational complexity of HODLR2D matrix-vector products remain tractable for large N. Additionally, we also present the parallel scalability of HODLR2D as part of this article.

Key takeaways
sparkles

AI

  1. HODLR2D offers a new hierarchical low-rank representation for dense matrices from 2D N-body problems.
  2. Matrix-vector products in HODLR2D scale as O(pN log(N)) with p ∈ O(log(N) log(log(N))).
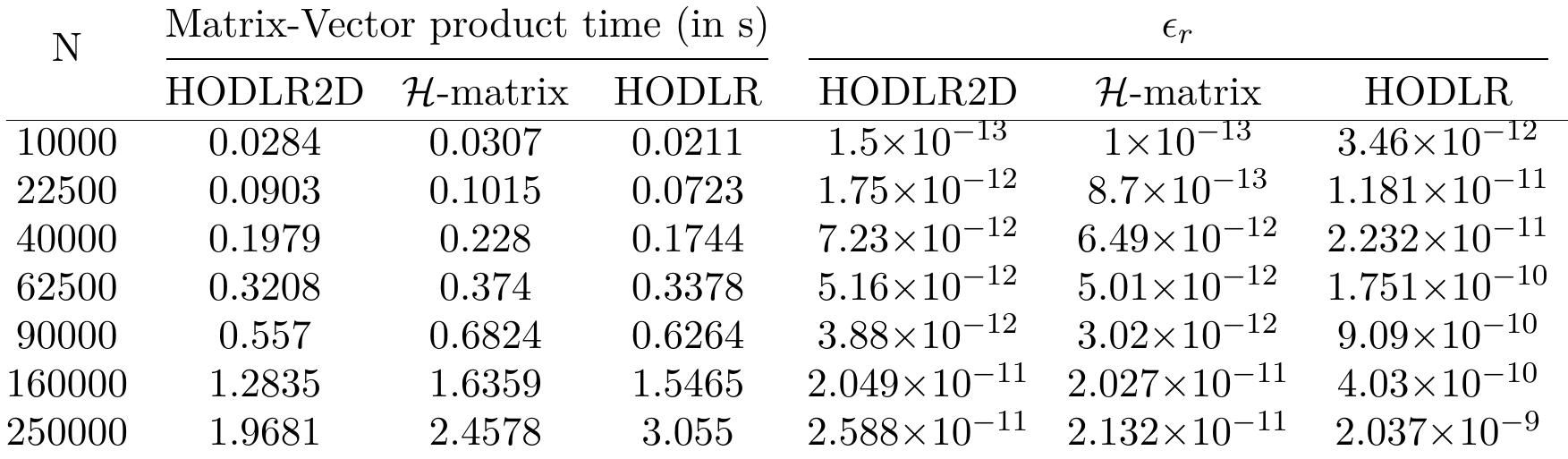
  3. HODLR2D improves computational efficiency, outperforming HODLR and H-matrix formats in both speed and storage.
  4. The algorithm demonstrates significant parallel scalability, enhancing performance on distributed systems.
  5. The study provides theorems supporting the growth of ranks for different interactions in 2D.
Figures (33)
3. Rank growth of different interactions in 2D Let’s now represent K as a 1 level HOLDR matrix. As mentioned before, HODLR uses a K- D tree, and hence at each level in the hierarchical tree, the box is subdivided into two smaller 2.3. HODLR matrix. We now describe the HODLR [5] matrix. The HODLR matrix approxi- mates the submatrix of interactions between any two disjoint clusters as a low-rank matrix. Typi- cally, the HODLR matrix subdivides the domain using a K-D tree. Following the conventions in [16], the 1-level HODLR representation of the dense matrix A € R‘** is given in Equation (2.2).
3. Rank growth of different interactions in 2D Let’s now represent K as a 1 level HOLDR matrix. As mentioned before, HODLR uses a K- D tree, and hence at each level in the hierarchical tree, the box is subdivided into two smaller 2.3. HODLR matrix. We now describe the HODLR [5] matrix. The HODLR matrix approxi- mates the submatrix of interactions between any two disjoint clusters as a low-rank matrix. Typi- cally, the HODLR matrix subdivides the domain using a K-D tree. Following the conventions in [16], the 1-level HODLR representation of the dense matrix A € R‘** is given in Equation (2.2).
0) ; boxes each containing n particles as shown in Figure 2. Hence, Bi is subdivided into two boxes BY = [-1,0) x [-1,1] and BY = (0, 1] x [—1,1] at level 1. Let the boxes BO BM each contain n =m? particles located at m x m Chebyshev grid, where m € Zt. Let Kz € R"*” represent the interaction of particles in Bw with the particles in Bo. FIGURE 3. Scaling of the rank of the off-diagonal block with the entries defined by log(r) to its size n
0) ; boxes each containing n particles as shown in Figure 2. Hence, Bi is subdivided into two boxes BY = [-1,0) x [-1,1] and BY = (0, 1] x [—1,1] at level 1. Let the boxes BO BM each contain n =m? particles located at m x m Chebyshev grid, where m € Zt. Let Kz € R"*” represent the interaction of particles in Bw with the particles in Bo. FIGURE 3. Scaling of the rank of the off-diagonal block with the entries defined by log(r) to its size n
FIGURE 2. Subdivision of box By” into BY and BY
FIGURE 2. Subdivision of box By” into BY and BY
FIGURE 6. Rank of Far field boxes The proof for this lemma can be found in [13, 27].
FIGURE 6. Rank of Far field boxes The proof for this lemma can be found in [13, 27].
FIGURE 8. Hierarchical subdivision of box B, FIGURE 7. Rank of vertex sharing boxes
FIGURE 8. Hierarchical subdivision of box B, FIGURE 7. Rank of vertex sharing boxes
FIGURE 11. Hierarchical subdivision of box By lying inside B,; are the respective columns of the matrix A and the columns corresponding to the charges lying outside B;,; are zeroes.
FIGURE 11. Hierarchical subdivision of box By lying inside B,; are the respective columns of the matrix A and the columns corresponding to the charges lying outside B;,; are zeroes.
FIGURE 12. Numerical Rank with « = 10~" of different interactions vs size of the off-diagonal block (n)
FIGURE 12. Numerical Rank with « = 10~" of different interactions vs size of the off-diagonal block (n)
FIGURE 13. Subdivision of the box B € R? at different levels and the numbering convention used We subdivide the domain using a quadtree. We begin by subdividing the square box B (the entire domain) into 4 smaller square boxes and number them as in Figure 13 and continue this till « levels. For each smaller box, the following definitions are intended to help us describe algorithms for HODLR2D matrices. Let C denote the cluster corresponding to the node i at level 1, NO as defined in Section 2.
FIGURE 13. Subdivision of the box B € R? at different levels and the numbering convention used We subdivide the domain using a quadtree. We begin by subdividing the square box B (the entire domain) into 4 smaller square boxes and number them as in Figure 13 and continue this till « levels. For each smaller box, the following definitions are intended to help us describe algorithms for HODLR2D matrices. Let C denote the cluster corresponding to the node i at level 1, NO as defined in Section 2.
FIGURE 14. Types of clusters at level 2 for a cluster considered Figure 14 illustrates different clusters for a cluster (coloured red) at level 2.
FIGURE 14. Types of clusters at level 2 for a cluster considered Figure 14 illustrates different clusters for a cluster (coloured red) at level 2.
FIGURE 15. Interaction relation of a cluster with other clusters for different levels. 4.1. HODLR2D Algorithm. Algorithm 1 provides the initialization routine of the HODLR2D based on quadtree. We start with the subdivision of the box corresponding to each the cluster into four geometrically disjoint boxes and number the resulting smaller boxes as in Figure 13. The Box B C R? is subdivided using a « level balanced quadtree such that all boxes at the leaf level have at most Nmax particles. Then for all the nodes in the Hierarchical tree, we form the set of Edge sharers (Ec) and the Interaction list (Ic). At all levels, we compress and represent the matrices corresponding to the elements in the Jc using ACA. The resulting low-rank approximation of the matrix at different levels using HODLR2D is as in Figure 16.
FIGURE 15. Interaction relation of a cluster with other clusters for different levels. 4.1. HODLR2D Algorithm. Algorithm 1 provides the initialization routine of the HODLR2D based on quadtree. We start with the subdivision of the box corresponding to each the cluster into four geometrically disjoint boxes and number the resulting smaller boxes as in Figure 13. The Box B C R? is subdivided using a « level balanced quadtree such that all boxes at the leaf level have at most Nmax particles. Then for all the nodes in the Hierarchical tree, we form the set of Edge sharers (Ec) and the Interaction list (Ic). At all levels, we compress and represent the matrices corresponding to the elements in the Jc using ACA. The resulting low-rank approximation of the matrix at different levels using HODLR2D is as in Figure 16.
TABLE 1. Space complexity of HODLR2D, H-matrix and HODLR for matrix K whose elements are defined by Equation (5.1) To demonstrate the computational performance of HODLR2D, H-matrix and HODLR, we use ten different input vectors ~) € R‘*!. We obtain the right-hand side vector b € R“*! using explicit matrix-vector product Ky = b. Let K represent the hierarchical low-rank representation of K and let the computed right hand side using the algorithm be b= Ky. Table 2 compares the computational performance of HODLR2D, H-matrix and HODLR using the average time taken for matrix-vector product on the ten different pair ~ € R‘*! and the error is the maximum relative error €,, 1.€., €- = max . The error reported in Table 2 is the maximum error over the ten u el |b, ‘ right hand sides. All the computations in this section were performed using only a single core of Intel Xeon Gold 6248. 20-ceore. 2.5 GHz processor with memorv of 1929GB.
TABLE 1. Space complexity of HODLR2D, H-matrix and HODLR for matrix K whose elements are defined by Equation (5.1) To demonstrate the computational performance of HODLR2D, H-matrix and HODLR, we use ten different input vectors ~) € R‘*!. We obtain the right-hand side vector b € R“*! using explicit matrix-vector product Ky = b. Let K represent the hierarchical low-rank representation of K and let the computed right hand side using the algorithm be b= Ky. Table 2 compares the computational performance of HODLR2D, H-matrix and HODLR using the average time taken for matrix-vector product on the ten different pair ~ € R‘*! and the error is the maximum relative error €,, 1.€., €- = max . The error reported in Table 2 is the maximum error over the ten u el |b, ‘ right hand sides. All the computations in this section were performed using only a single core of Intel Xeon Gold 6248. 20-ceore. 2.5 GHz processor with memorv of 1929GB.
TABLE 2. Computational performance of HODLR2D, H-matrix and HODLR for matrix K whose elements are defined by Equation (5.1)
TABLE 2. Computational performance of HODLR2D, H-matrix and HODLR for matrix K whose elements are defined by Equation (5.1)
5.2. HODLR2D accelerated iterative solver for radial basis function interpolation. All the numerical experiments in this and the next subsection are performed without parallelization on a laptop with a 2.5GHz Intel Core i5 processor and 16GB RAM. a _ -_ = es
5.2. HODLR2D accelerated iterative solver for radial basis function interpolation. All the numerical experiments in this and the next subsection are performed without parallelization on a laptop with a 2.5GHz Intel Core i5 processor and 16GB RAM. a _ -_ = es
TABLE 4. Time taken for the iterative solver Tg to solve Equation (5.2) for ¢1(r)
TABLE 4. Time taken for the iterative solver Tg to solve Equation (5.2) for ¢1(r)
TABLE 5. Space complexity of HODLR2D, H-matrix and HODLR for ¢2(r)
TABLE 5. Space complexity of HODLR2D, H-matrix and HODLR for ¢2(r)
FIGURE 18. rm for HODLR2D, H-matrix and HODLR for both radial basis func- tions
FIGURE 18. rm for HODLR2D, H-matrix and HODLR for both radial basis func- tions
FIGURE 19. Storage for HODLR2D, H-matrix and HODLR for both radial basis functions
FIGURE 19. Storage for HODLR2D, H-matrix and HODLR for both radial basis functions
where wo is a vector of values of w(x) at the grid points located in the leaf boxes of the quadtree as done in [28, 29]. As done in [28, 29], we hierarchically subdivide the domain into smaller domains using a level restricted quadtree and represent the unknown function w(x) as polynomials on each of the leaf boxes of the level restricted quadtree. For our numerical experiments, we varied the number of levels in the level restricted quadtree and the number of points in the leaf level of the level restricted quadtree. It is to be noted that the level restricted quadtree mentioned here is in the context of discretizing the domain. The HODLR2D hierarchical low-rank structure still rests on the balanced quadtree as discussed in the previous section.
where wo is a vector of values of w(x) at the grid points located in the leaf boxes of the quadtree as done in [28, 29]. As done in [28, 29], we hierarchically subdivide the domain into smaller domains using a level restricted quadtree and represent the unknown function w(x) as polynomials on each of the leaf boxes of the level restricted quadtree. For our numerical experiments, we varied the number of levels in the level restricted quadtree and the number of points in the leaf level of the level restricted quadtree. It is to be noted that the level restricted quadtree mentioned here is in the context of discretizing the domain. The HODLR2D hierarchical low-rank structure still rests on the balanced quadtree as discussed in the previous section.
Since the right-hand side vector is well defined for this example, we use GMRES with stopping criteria as residual being 10~!° to get an approximate solution vector. The approximate solution vector is again used to generate the right-hand side by explicitly constructing the dense matrix and performing a matrix-vector product. The error reported in Table 8 is the relative forward error in the solution vector w. 5.4. Inferences. The key observation from the Tables 3 through 8 is that the maximum rank reported remains almost constant in the case of H#-matrix and HODLR2D, whereas for HODLR, it increases as a function of the system size. From Figures 17 through 21, it is clear that HODLR2D scales almost linearly in terms of both storage and computational complexity. In all examples considered, HODLR2D performs significantly better in space and computational complexity than HODLR and provides an attractive alternative to H-matrix.
Since the right-hand side vector is well defined for this example, we use GMRES with stopping criteria as residual being 10~!° to get an approximate solution vector. The approximate solution vector is again used to generate the right-hand side by explicitly constructing the dense matrix and performing a matrix-vector product. The error reported in Table 8 is the relative forward error in the solution vector w. 5.4. Inferences. The key observation from the Tables 3 through 8 is that the maximum rank reported remains almost constant in the case of H#-matrix and HODLR2D, whereas for HODLR, it increases as a function of the system size. From Figures 17 through 21, it is clear that HODLR2D scales almost linearly in terms of both storage and computational complexity. In all examples considered, HODLR2D performs significantly better in space and computational complexity than HODLR and provides an attractive alternative to H-matrix.
where n denotes the number of points in the cluster and m; denotes number of points in 7” cluster in I¢ and finally k; denotes number of points in j*” cluster in Ec. Upon estimating the load for each node, we schedule the nodes across the processors by prioritizing the node with largest load first and by maintaining the load per processor almost constant. It is important to note that the scheduling is done apriori and not dynamically, the reason being it suits well for hybrid (multi-core + distributed) architectures. The initialization for HODLR2D does not require communication between the MPI processes. This section will examine the parallel scalability of HODLR2D initialization (Algorithm 1) and the matrix-vector product (Algorithm 2) on distributed memory systems. The existing literature on the parallel scalability of the rank structured matrices (both flat and hierarchical formats) is extensive, and we direct our readers to some seminal work[30, 31, 32, 33]. An important factor in the parallel scalability of an algorithm is how efficiently we can divide the load across the processes. In our case, we perform this by estimating the load of each node in the quadtree using Equation (6.1).
where n denotes the number of points in the cluster and m; denotes number of points in 7” cluster in I¢ and finally k; denotes number of points in j*” cluster in Ec. Upon estimating the load for each node, we schedule the nodes across the processors by prioritizing the node with largest load first and by maintaining the load per processor almost constant. It is important to note that the scheduling is done apriori and not dynamically, the reason being it suits well for hybrid (multi-core + distributed) architectures. The initialization for HODLR2D does not require communication between the MPI processes. This section will examine the parallel scalability of HODLR2D initialization (Algorithm 1) and the matrix-vector product (Algorithm 2) on distributed memory systems. The existing literature on the parallel scalability of the rank structured matrices (both flat and hierarchical formats) is extensive, and we direct our readers to some seminal work[30, 31, 32, 33]. An important factor in the parallel scalability of an algorithm is how efficiently we can divide the load across the processes. In our case, we perform this by estimating the load of each node in the quadtree using Equation (6.1).
TABLE 9. HODLR2D Initialization time (in seconds) for different system sizes (N’ by varying number of processors
TABLE 9. HODLR2D Initialization time (in seconds) for different system sizes (N’ by varying number of processors
FIGURE 22. Speedup of parallel HODLR2D vs number of MPI processor TABLE 10. HODLR2D Mat-Vec time (in seconds) for different system sizes (N) by varying number of processors
FIGURE 22. Speedup of parallel HODLR2D vs number of MPI processor TABLE 10. HODLR2D Mat-Vec time (in seconds) for different system sizes (N) by varying number of processors

Related papers

A Fast Direct Solver for Structured Linear Systems by Recursive Skeletonization
Leslie Greengard

SIAM Journal on Scientific Computing, 2012

We present a fast direct solver for structured linear systems based on multilevel matrix compression. Using the recently developed interpolative decomposition of a low-rank matrix in a recursive manner, we embed an approximation of the original matrix into a larger, but highly structured sparse one that allows fast factorization and application of the inverse. The algorithm extends the Martinsson/Rokhlin method developed for 2D boundary integral equations and proceeds in two phases: a precomputation phase, consisting of matrix compression and factorization, followed by a solution phase to apply the matrix inverse. For boundary integral equations which are not too oscillatory, e.g., based on the Green's functions for the Laplace or low-frequency Helmholtz equations, both phases typically have complexity O(N) in two dimensions, where N is the number of discretization points. In our current implementation, the corresponding costs in three dimensions are O(N 3/2) and O(N log N) for precomputation and solution, respectively. Extensive numerical experiments show a speedup of ∼ 100 for the solution phase over modern fast multipole methods; however, the cost of precomputation remains high. Thus, the solver is particularly suited to problems where large numbers of iterations would be required. Such is the case with ill-conditioned linear systems or when the same system is to be solved with multiple right-hand sides. Our algorithm is implemented in Fortran and freely available.

View PDFchevron_right
Application of hierarchical matrices for solving multiscale problems
Alexander Litvinenko
View PDFchevron_right
Low-Complexity Direct and Iterative Volume Integral Equation Solvers With a Minimal-Rank ${\mathcal H}^2$-Representation for Large-Scale Three-Dimensional Electrodynamic Analysis
Saad Omar

IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2017

Low-complexity iterative and direct solvers are developed for the volume integral equation (VIE) based general large-scale electrodynamic analysis. The dense VIE system matrix is first represented by a new cluster-based multilevel lowrank representation. In this representation, all the admissible blocks associated with a single cluster are grouped together and represented by a single low-rank block, whose rank is minimized based on prescribed accuracy. From such an initial representation, an efficient algorithm is developed to generate a minimal-rank H 2-matrix representation. This representation facilitates faster computation, and ensures the same minimal rank's growth rate with electrical size as evaluated from singular value decomposition. For a minimal-rank representation whose rank grows with electrical size linearly for a prescribed accuracy, we develop linear-complexity H 2-matrix-based storage and matrix-vector multiplication, and thereby an O(N) iterative VIE solver. Moreover, we develop an O(NlogN) matrix inversion, and hence a fast O(NlogN) direct VIE solver for large-scale electrodynamic analysis. Both theoretical analysis and numerical simulations of large-scale 1-, 2and 3-D structures on a singlecore CPU, resulting in millions of unknowns, have demonstrated the low complexity and superior performance of the proposed VIE electrodynamic solvers.

View PDFchevron_right
Hierarchical Orthogonal Matrix Generation and Matrix-Vector Multiplications in Rigid Body Simulations
Gary Huber

2017

In this paper, we apply the hierarchical modeling technique and study some numerical linear algebra problems arising from the Brownian dynamics simulations of biomolecular systems where molecules are modeled as ensembles of rigid bodies. Given a rigid body p consisting of n beads, the 6 × 3n transformation matrix Z that maps the force on each bead to p's translational and rotational forces (a 6× 1 vector), and V the row space of Z, we show how to explicitly construct the (3n-6) × 3n matrix Q̃ consisting of (3n-6) orthonormal basis vectors of V^ (orthogonal complement of V) using only O(n n) operations and storage. For applications where only the matrix-vector multiplications Q̃ v and Q̃^T v are needed, we introduce asymptotically optimal O(n) hierarchical algorithms without explicitly forming Q̃. Preliminary numerical results are presented to demonstrate the performance and accuracy of the numerical algorithms.

View PDFchevron_right
A Fast Solver for HSS Representations via Sparse Matrices
Shivkumar Chandrasekaran

SIAM Journal on Matrix Analysis and Applications, 2007

In this paper we present a fast direct solver for certain classes of dense structured linear systems that works by first converting the given dense system to a larger system of block sparse equations and then uses standard sparse direct solvers. The kind of matrix structures that we consider are induced by numerical low rank in the off-diagonal blocks of the matrix and are related to the structures exploited by the fast multipole method (FMM) of Greengard and Rokhlin. The special structure that we exploit in this paper is captured by what we term the hierarchically semiseparable (HSS) representation of a matrix. Numerical experiments indicate that the method is probably backward stable.

View PDFchevron_right
A Tensor-Train accelerated solver for integral equations in complex geometries
Eduardo Corona

Journal of Computational Physics

We present a framework using the Quantized Tensor Train (QTT) decomposition to accurately and efficiently solve volume and boundary integral equations in three dimensions. We describe how the QTT decomposition can be used as a hierarchical compression and inversion scheme for matrices arising from the discretization of integral equations. For a broad range of problems, computational and storage costs of the inversion scheme are extremely modest O log N and once the inverse is computed, it can be applied in O N log N. We analyze the QTT ranks for hierarchically low rank matrices and discuss its relationship to commonly used hierarchical compression techniques such as FMM and HSS. We prove that the QTT ranks are bounded for translation-invariant systems and argue that this behavior extends to nontranslation invariant volume and boundary integrals. For volume integrals, the QTT decomposition provides an efficient direct solver requiring significantly less memory compared to other fast direct solvers. We present results demonstrating the remarkable performance of the QTT-based solver when applied to both translation and non-translation invariant volume integrals in 3D. For boundary integral equations, we demonstrate that using a QTT decomposition to construct preconditioners for a Krylov subspace method leads to an efficient and robust solver with a small memory footprint. We test the QTT preconditioners in the iterative solution of an exterior elliptic boundary value problem (Laplace) formulated as a boundary integral equation in complex, multiply connected geometries.

View PDFchevron_right
O(N) Iterative and O(NlogN) Fast Direct Volume
Saad Omar

2017

Linear complexity iterative and log-linear complexity direct solvers are developed for the volume integral equation (VIE) based general large-scale electrodynamic analysis. The dense VIE system matrix is first represented by a new clusterbased multilevel low-rank representation. In this representation, all the admissible blocks associated with a single cluster are grouped together and represented by a single low-rank block, whose rank is minimized based on prescribed accuracy. From such an initial representation, an efficient algorithm is developed to generate a minimal-rank H 2-matrix representation. This representation facilitates faster computation, and ensures the same minimal rank's growth rate with electrical size as evaluated from singular value decomposition. Taking into account the rank's growth with electrical size, we develop linear-complexity H 2-matrix-based storage and matrix-vector multiplication, and thereby an O(N) iterative VIE solver regardless of electrical size. Moreover, we develop an O(N logN) matrix inversion, and hence a fast O(N logN) direct VIE solver for large-scale electrodynamic analysis. Both theoretical analysis and numerical simulations of large-scale 1-, 2-and 3-D structures on a singlecore CPU, resulting in millions of unknowns, have demonstrated the low complexity and superior performance of the proposed VIE electrodynamic solvers.

View PDFchevron_right
Fast multilevel sparse Gaussian kernels for high-dimensional approximation and integration
Jeremy Levesley

A fast multilevel algorithm based on directionally scaled tensor-product Gaussian kernels on structured sparse grids is proposed for interpolation of high-dimensional functions and for the numerical integration of high-dimensional integrals. The algorithm is based on the recent Multilevel Sparse Kernel-based Interpolation (MLSKI) method (Georgoulis, Levesley & Subhan, SIAM J. Sci. Comput., 35(2), pp. A815-A831, 2013), with particular focus on the fast implementation of Gaussianbased MLSKI for interpolation and integration problems of high-dimensional functions f : [0, 1] d → R, with 5 ≤ d ≤ 10. The MLSKI interpolation procedure is shown to be interpolatory and a fast implementation is proposed. More specifically, exploiting the tensor-product nature of anisotropic Gaussian kernels, one-dimensional cardinal basis functions on a sequence of hierarchical equidistant nodes are precomputed to machine precision, rendering the interpolation problem into a fully parallelisable ensemble of linear combinations of function evaluations. A numerical integration algorithm is also proposed, based on interpolating the (highdimensional) integrand. A series of numerical experiments highlights the applicability of the proposed algorithm for interpolation and integration for up to 10-dimensional problems.

View PDFchevron_right
Iterative solution methods based on the hierarchically semi-separable representation
Nick van der Meijs

2006

In this paper, we study an important class of structured matrices: "Hierarchically Semi-Separable (HSS)" matrices, for which an efficient hierarchical state based representation called Hierarchically Semi-Separable (HSS) representation can be used to utilize the data sparsity of the HSS matrices. A novel algorithm with O(n) complexity is proposed to construct suboptimal HSS representations from sparse matrices. Subsequently, the limitation of the direct HSS solution method is discussed in this paper, and a general strategy to combine standard iterative solution methods with the HSS representation is presented. We also describe a number of preconditioner construction algorithms based on the HSS representation. Our numerical experiments indicate that these iterative solution methods have linear complexity in computation time.

View PDFchevron_right
A discrete adapted hierarchical basis solver for radial basis function interpolation
Victor Eijkhout

BIT Numerical Mathematics, 2013

In this paper we develop a discrete Hierarchical Basis (HB) to efficiently solve the Radial Basis Function (RBF) interpolation problem with variable polynomial order. The HB forms an orthogonal set and is adapted to the kernel seed function and the placement of the interpolation nodes. Moreover, this basis is orthogonal to a set of polynomials up to a given order defined on the interpolating nodes. We are thus able to decouple the RBF interpolation problem for any order of the polynomial interpolation and solve it in two steps: (1) The polynomial orthogonal RBF interpolation problem is efficiently solved in the transformed HB basis with a GMRES iteration and a diagonal, or block SSOR preconditioner. (2) The residual is then projected onto an orthonormal polynomial basis. We apply our approach on several test cases to study its effectiveness, including an application to the Best Linear Unbiased Estimator regression problem.

View PDFchevron_right

References (33)

  1. W. Hackbusch. Sparse matrix arithmetic based on H-matrices. part i: Introduction to H-matrices. Computing (Vienna/New York), 62(2):89-108, 1999.
  2. L. Grasedyck and W. Hackbusch. Construction and arithmetics of H-matrices. Computing (Vienna/New York), 70(4):295-334, 2003.
  3. Nail A Gumerov and Ramani Duraiswami. Fast radial basis function interpolation via preconditioned Krylov iteration. SIAM Journal on Scientific Computing, 29(5):1876-1899, 2007.
  4. V Rokhlin. Rapid solution of integral equations of scattering theory in two dimensions. Journal of Computational Physics, 86(2):414-439, 1990.
  5. Sivaram Ambikasaran, Judith Yue Li, Peter K Kitanidis, and Eric Darve. Large-scale stochastic linear inversion using hierarchical matrices. Computational Geosciences, 17(6):913-927, 2013.
  6. Alexander Gray and Andrew Moore. N-body problems in statistical learning. Advances in neural information processing systems, 13, 2000.
  7. Sivaram Ambikasaran, Michael O'Neil, and Karan Raj Singh. Fast symmetric factorization of hierarchical ma- trices with applications, 2016.
  8. Josh Barnes and Piet Hut. A hierarchical O (n log n) force-calculation algorithm. nature, 324(6096):446-449, 1986.
  9. L. Greengard and V. Rokhlin. A fast algorithm for particle simulations. Journal of Computational Physics, 73(2):325-348, 1987.
  10. Wolfgang Hackbusch and Z. Nowak. On the fast multiplication in the boundary element method by panel clustering. Numerische Mathematik, 54:463-491, 07 1989.
  11. Eric Darve. The fast multipole method: Numerical implementation. Journal of Computational Physics, 160(1):195-240, may 2000.
  12. William Fong and Eric Darve. The black-box fast multipole method. Journal of Computational Physics, 228(23):8712-8725, dec 2009.
  13. Rick Beatson and Leslie Greengard. A short course on fast multipole methods. In Wavelets, Multilevel Methods and Elliptic PDEs, pages 1-37. Oxford University Press, 1997.
  14. Rio Yokota, Huda Ibeid, and David Keyes. Fast multipole method as a matrix-free hierarchical low-rank approxi- mation. In International Workshop on Eigenvalue Problems: Algorithms, Software and Applications in Petascale Computing, pages 267-286. Springer, 2015.
  15. Per-Gunnar Martinsson and Vladimir Rokhlin. An accelerated kernel-independent fast multipole method in one dimension. SIAM Journal on Scientific Computing, 29(3):1160-1178, 2007.
  16. Sivaram Ambikasaran and Eric Darve. An O(n log n) -fast direct solver for partial hierarchically semi-separable matrices. Journal of Scientific Computing, 57(3):477-501, apr 2013.
  17. Sivaram Ambikasaran and Eric Darve. The inverse fast multipole method, 2014.
  18. Shiv Chandrasekaran, Patrick Dewilde, Ming Gu, T Pals, and Alle-Jan van der Veen. Fast stable solver for sequentially semi-separable linear systems of equations. In International Conference on High-Performance Com- puting, pages 545-554. Springer, 2002.
  19. Adrianna Gillman, Patrick M Young, and Per-Gunnar Martinsson. A direct solver with O(n) complexity for integral equations on one-dimensional domains. Frontiers of Mathematics in China, 7(2):217-247, 2012.
  20. S. Börm. Construction of data-sparse H 2 -matrices by hierarchical compression. SIAM Journal on Scientific Computing, 31(3):1820-1839, 2009. cited By 26.
  21. Mario Bebendorf and Raoul Venn. Constructing nested bases approximations from the entries of non-local operators. Numerische Mathematik, 121(4):609-635, 2012.
  22. Yu Zhao, Dan Jiao, and Junfa Mao. Fast nested cross approximation algorithm for solving large-scale electro- magnetic problems. IEEE Transactions on Microwave Theory and Techniques, 67(8):3271-3283, 2019.
  23. Vaishnavi Gujjula and Sivaram Ambikasaran. A new nested cross approximation. arXiv preprint arXiv:2203.14832, 2022.
  24. M. Bebendorf and S. Rjasanow. Adaptive low-rank approximation of collocation matrices. Computing, 70(1):1- 24, feb 2003.
  25. Kezhong Zhao, M.N. Vouvakis, and Jin-Fa Lee. The adaptive cross approximation algorithm for accelerated method of moments computations of emc problems. IEEE Transactions on Electromagnetic Compatibility, 47(4):763-773, 2005.
  26. Sivaram Ambikasaran, Karan Raj Singh, and Shyam Sundar Sankaran. Hodlrlib: A library for hierarchical matrices. Journal of Open Source Software, 4(34):1167, 2019.
  27. L Greengard and V Rokhlin. A fast algorithm for particle simulations. Journal of Computational Physics, 73(2):325-348, dec 1987.
  28. Sivaram Ambikasaran, Carlos Borges, Lise-Marie Imbert-Gerard, and Leslie Greengard. Fast, adaptive, high- order accurate discretization of the lippmann-schwinger equation in two dimensions. SIAM Journal on Scientific Computing, 38(3):A1770-A1787, jan 2016.
  29. Vaishnavi Gujjula and Sivaram Ambikasaran. A new directional algebraic fast multipole method based it- erative solver for the lippmann-schwinger equation accelerated with HODLR preconditioner. arXiv preprint arXiv:2204.00326, 2022.
  30. A. Ida, T. Iwashita, T. Mifune, and Y. Takahashi. Parallel hierarchical matrices with adaptive cross approxi- mation on symmetric multiprocessing clusters. Journal of Information Processing, 22(4):642-650, 2014. cited By 24.
  31. Patrick R Amestoy, Alfredo Buttari, Jean-Yves L'excellent, and Theo Mary. Performance and scalability of the block low-rank multifrontal factorization on multicore architectures. ACM Transactions on Mathematical Software (TOMS), 45(1):1-26, 2019.
  32. Kadir Akbudak, Hatem Ltaief, Aleksandr Mikhalev, and David Keyes. Tile low rank cholesky factorization for climate/weather modeling applications on manycore architectures. In International Supercomputing Conference, pages 22-40. Springer, 2017.
  33. Mohammad Izadi. Hierarchical matrix techniques on massively parallel computers. Ph.D. thesis, Max Planck Institute for Mathematics in the Sciences, 2012.

Related papers

Fast construction of hierarchical matrix representation from matrix–vector multiplication
lin lin

Journal of Computational Physics, 2011

We develop a hierarchical matrix construction algorithm using matrixvector multiplications, based on the randomized singular value decomposition of low-rank matrices. The algorithm uses O(log n) applications of the matrix on structured random test vectors and O(n log n) extra computational cost, where n is the dimension of the unknown matrix. Numerical examples on constructing Green's functions for elliptic operators in two dimensions show efficiency and accuracy of the proposed algorithm.

View PDFchevron_right
Parallel matrix-vector product using approximate hierarchical methods
Ahmed Sameh

Proceedings of the 1995 ACM/IEEE conference on Supercomputing (CDROM) - Supercomputing '95, 1995

Matrix-vector products (mat-vecs) form the core of iterative methods used for solving dense linear systems. Often, these systems arise in the solution of integral equations used in electromagnetics, heat transfer, and wave propagation. In this paper, we present a parallel approximate method for computing mat-vecs used in the solution of integral equations. We use this method to compute dense mat-vecs of hundreds of thousands of elements. The combined speedups obtained from the use of approximate methods and parallel processing represent an improvement of several orders of magnitude over exact mat-vecs on uniprocessors. We demonstrate that our parallel formulation incurs minimal parallel processing overhead and scales up to a large number of processors. We study the impact of varying the accuracy of the approximate mat-vec on overall time and on parallel efficiency.

View PDFchevron_right
Accelerating Matrix-Vector Multiplication on Hierarchical Matrices Using Graphical Processing Units
Alexander Litvinenko
View PDFchevron_right
A Low-Rank IE-QR Algorithm for Matrix Compression in Volume Integral Equations
Jin-Fa Lee

IEEE Transactions on Magnetics, 2004

View PDFchevron_right
Fast and efficient parallel solution of dense linear systems
John Reif

Computers & Mathematics with Applications, 1989

View PDFchevron_right

Related topics

  • Mathematics
  • Computer Science
  • Computational Complexity Theory
    • 580 California St., Suite 400
    San Francisco, CA, 94104
    © 2025 Academia. All rights reserved