Structural Optimization of Truss Using Finite Element Analysis
2018, IEEE
https://doi.org/10.1109/ICSCET.2018.8537295…
5 pages
1 file
Sign up for access to the world's latest research
Abstract
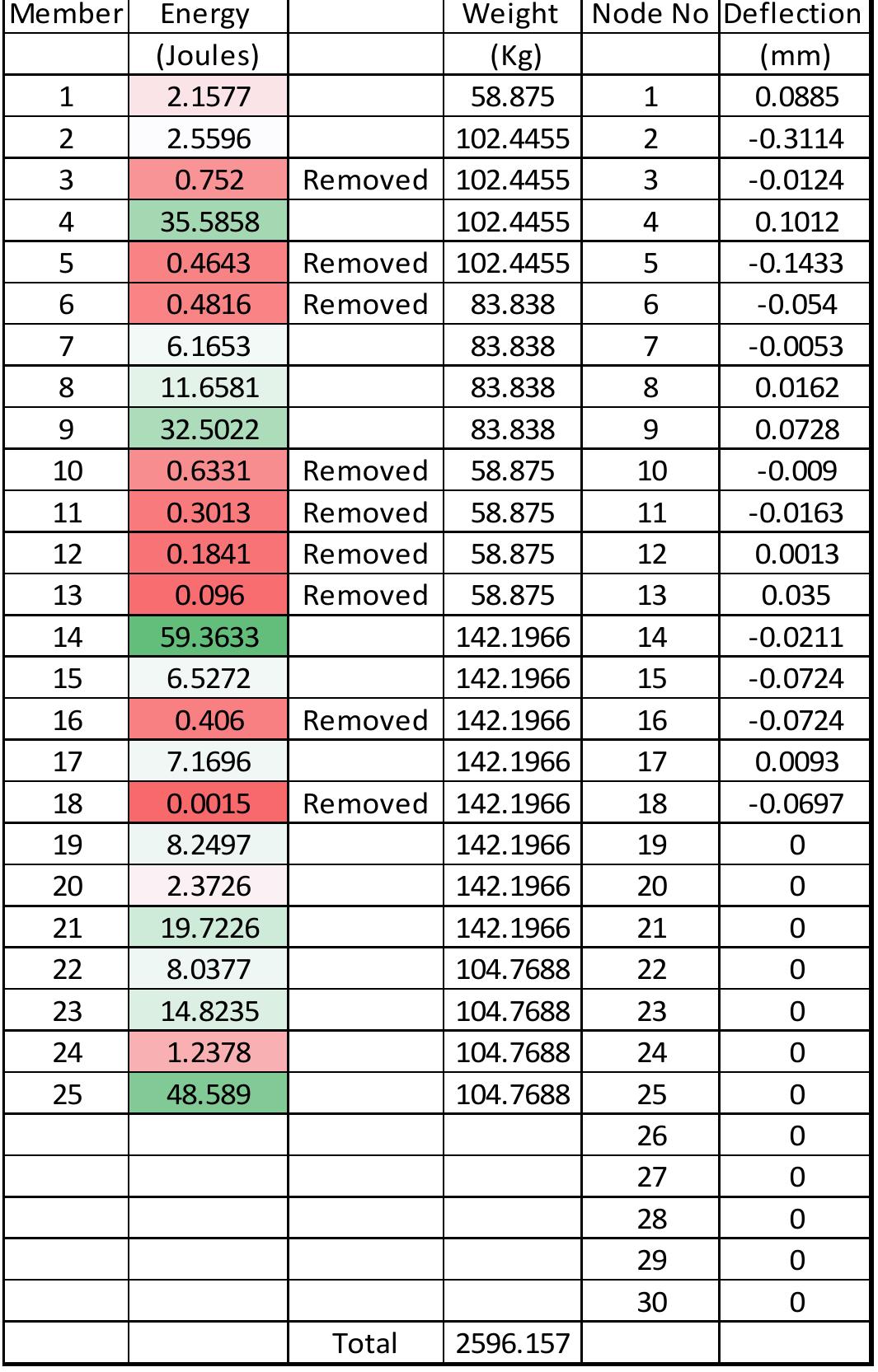
Trusses are most commonly used structure in industrial buildings, warehouses, bridges, transmission tower etc. There are different types of trusses available for construction. The analysis and design of an economical and stable truss system for utilization in industrial buildings., storage rooms., bridges., warehouses., transmission towers etc. is necessary. The present study is done on static analysis and optimization of truss system to get optimal and economical configuration of truss. Total cost of the structure depends upon mass of the structure and mass is directly relative to the material consumed by the skeleton of the structure. This paper presents the use of programming language MATLAB for static analysis of truss structure using “Finite Element Method” and the ‘Topology Optimization’ will be done based on the energy stored in the member. Static analysis of a 13 bar benchmark truss is done using MATLAB programming code and various results have been obtained. After interpret...













Related papers
IOP Conference Series: Materials Science and Engineering, 2018
The paper presents a new algorithm for size optimization of the trusses using finite element method. The objective function was established based on weight minimization of trusses. The constraint conditions were formulated based on the conditions that the structure satisfies the strength, stiffness and compatibility requirements, and equilibrium equations. Determination of internal forces, displacements and establishment of the equations are based on finite element method. In order to solve optimization problems using finite element method, the authors proposed a new method for seeking optimal solutions. For truss weight optimization, the authors proposed a coefficient and called this coefficient as "the correlation coefficient of internal forces among truss elements". This coefficient shows the relationship between the internal forces of truss elements, which was used as the basis for re-selecting the dimensions of cross section of truss elements in iterative process. The paper introduces the calculation procedure and analysis algorithm for weight optimization of planar and space trusses. The examples for weight optimization of planar and space trusses were implemented in a subroutine written in Matlab software. The calculation results using the method proposed by the authors matched with the calculation results using other methods such as Hybridized Genetic Algorithm, Harmony search method, HyperWork, etc. However, using the method proposed by the authors gives less iterative circles.
REM - International Engineering Journal
Seeking to define more robust and executable structures, this article presents a computational framework for the optimal design of steel truss frames, which integrates two software of great prominence in structural engineering, MATLAB and ANSYS. Computational interfaces were created to enable the automation of the iterative optimization process. The optimization algorithm and computational interfaces were developed on the MATLAB platform, while structural analyses were performed with the ANSYS Mechanical APDL platform. Some details of the computational implementation are presented herein. The objective is to minimize the cost of structures by determining the optimal positioning of nodal coordinates and the optimal choice of commercially available structural profiles-shape and size optimization, respectively. For shape optimization, a computational model was defined to automatically generate the geometry of the structure, maintaining some intrinsic relations of symmetry and collinearity between elements. The design constraints are critical nodal displacements, stresses, and slenderness of elements, following the requirements of ABNT NBR 8800:2008. To exemplify the application of the proposed methodology, this article presents the optimal design of trusses for roofs of industrial sheds, considering its non-linear geometric behavior, typical of this type of structure.
Minimizing Weight by Optimizing Different Truss Parts Using Finite Element Analysis, 2024
This paper presents a study of minimizing weight by optimizing different truss parts using finite element analysis and comparing Warren trusses with other trusses. The aim of the optimization is to find a light design. Existing structural steel trusses were initially optimized for minimum weight and constrained with allowable stresses and deflections. Applicable Eurocode 3 design conditions are presented, which provide the constraints for the problem. Steel truss is a preferred solution in large-span roof structures due to its good attributes, such as being lightweight and durable. Existing structural steel trusses were initially optimized for minimum weight and constrained with allowable stresses and deflections. Constant spans of the trusses have been considered, and each truss has been subjected to the same types of load cases. The top chord member load has been kept constant in each truss at 2 kN/m. Two sets of load conditions are taken as the self-weight of the truss and the snow load, but the structure is calculated by the load combination. The structural steel trusses were optimized using the design optimization tool as a first-order optimization method in RFEM, and it was extended to compare the most suitable truss geometry for the minimum weight. Finally, it is concluded that the Warren truss has a higher stiffness-to-weight ratio than other trusses after optimization. The goal of this study was to analyze all trusses and ensure that the structural stress is less than the allowable stress and that the deflection is less than the allowable deflection. The span and height are constant in all cases because they have no impact on the weight increase; only the position of the rods and cross-section size affect the building's ability to withstand loads and weight increases. In this paper, a finite element analysis (FEA)-based optimization technique is proposed for the optimization of a light design that is constrained by allowable stresses and deflections. For this purpose, there have been studies on sizing optimization to minimize the mass of different steel truss roof system types both in the past and today. For this purpose, weight design and analysis of the optimum weight are carried out on ten different
The optimal design of skeletal structure becomes imperative both from engineering and cost considerations in recent year. Total cost of the structure mainly depends on weight of the structure and weight of the structure is proportional to material distribution within the structure.
MATEC Web of Conferences
The article presents a comparison of results of optimized calculation of a truss beam which was chosen as a combined construction. The results of calculation of a beam are compared using the method based on the properties of spacer systems and the calculation of the construction designed in LIRA software complex. The article is dedicated to verification of adequacy of the results of theoretical calculations of construction optimization. Values of longitudinal forces and bending moments appearing in a truss beam are chosen as convergence criteria. Two variants of construction loading are considered: a truss beam exposed to constant load only and a truss beam exposed to constant and temporary load. In the case under consideration, the minimum value (weight) of construction is an optimality criteria, variable parameters include beam panel length and camber height of a trussing rod. As a result, the construction will be considered optimal, if bearing and maximal (between the pillars) be...
2016
In this paper the static analysis of the truss is investigated. The analytical and computational method of the roof structures are presented. At the beginning, the analytical method is used for determination of values of external supports, axial forces and principal stresses in truss. Then the computational method is used for the solution of the same problems. The roof structure is modeled by the finite element method, where the bar members are represented by the truss elements. The finite element model loaded by external forces, without and with self-weight of structure is computed. At the end, the analytical and computational buckling analysis for the trusses with maximal compressive axial force is performed. The comparison of results of analytical and computational method shows that all methods are accurate enough, but of course computational method is faster and more adaptive for any subsequent changes.
IRJET, 2022
There are numerous advantages to using steel trusses instead of traditional wood trusses but the main reasons are simplicity and strength. Using steel can help to create a stronger structure that is able to stand up to not only more weight but also higher winds providing more protection that other options. Steel trusses are merely outlined as triangulation of members to form the stable structure. Triangulation is that the stable configuration mathematically. Though there are several parts of a truss bridge the use of materials is very effective. Elements like iron, wood, steel as well as iron are all used to their highest potential and eadarch of the pieces plays an important role in it. The buildings of a bridge can be a useful option, while compared to other types of bridges. The main objective of this study is to determine the most economical and efficient type of steel truss bridge along with different type of steel. The analysis is carried out in the Staad-pro with reference to the Indian standard code of steel design.
Engineering structures is an important aspect of human civilization and manual analysis of structure often deviates from actual value, so there is a need to use Finite Element Method technique for analyzing those structures. Thus, this paper presents FEM based codes developed in MATLAB programming which targets the analysis of 2D linear, elastic-isotropic structure. This program lists the results of displacement, stress-strain, reaction forces and plots the deformed shaped due to applied forces. Since the software is solitary only on truss analysis, it computes faster compare to other market software like ANSYS, COMSOL etc. Keywords—linear structure, finite element method, MATLAB programming
Journal of Software Engineering & Intelligent Systems, 2017
An important aspect of any engineering design problem is to achieve efficiency and efficacy. This can be in terms of energy consumption, performance, time, total weight and costs. In many cases, there are multiple solutions to a problem and you should select the one which satisfies better the criteria. This engineering design process is known as optimization. Optimization plays an important role in various engineering applications. Engineers are in continuity, challenged to design structures that use the least amount of resources and satisfy the structural requirements. The optimal design of structures can be decomposed into three major categories: topology, shape and size optimization. These methods have evolved with time and they may be divided in two maxi-groups: deterministic and non-deterministic algorithms. Size optimization of non-deterministic methods with genetic algorithms (GA) are investigated in this article and applied to some steel trusses in MATLAB soft R2017a. This is done by building an algorithm consisting in scripts and sub-functions, which are applied to the trusses for different constraints on stresses, displacements and buckling, depending on the case analyzed. Different values for the GA parameters are analyzed in such way to achieve the best design. The results are put in comparison with previous studies.
International Journal of Scientific & Technology Research, 2020
Structural design optimization is a mathematical approach that concerns in finding the maxima and minima function subject to some constraints. This involves various optimization technique to find the best possible design in terms of weight, reliability and thus the overall cost. Various researchers have worked on different optimization techniques in finding out the efficient and light weight structures that are essential for the actual design of tall structures. This paper summarizes the various techniques of optimization of steel truss or towers that have been used till now. For this purpose, different optimization techniques have been studied which involves the various geometric constraints like changing the base width, bracing pattern, area of cross section. By reviewing the literature of the works done, the common objective emphasizes the need for finding the minimum weight of the structure. From studies we see optimization using metaheuristic algorithm are effective in order to solve truss problems. Metaheuristic algorithms are nature-inspired and most widely used due to its applicability and feasibility to various types of structures with many numbers of design variables. In this paper a 25-bar space benchmark truss has been considered for demonstrating the performance of various optimization algorithm. A comparative study is done based on the performance in lowering the weight of the total truss. Results shows that optimal weight of the truss structure can be obtained effectively using Whale optimization algorithm and it proved to be robust and efficient than other algorithms.

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
References (5)
- Kalyanmoy Deb and Gulati, Surendra, Design of Truss Structures for Minimum Weight Using Genetic Algorithms, Finite Elements in Analysis and Design. Volume 37, issue 5. Pp. 447-465. (2000).
- Achtziger, W., Topology optimization of discrete structures -An introduction in view of computational and nonsmooth aspects, in Topology Optimization in Structural Mechanics, G.I.N. Rozvany (ed.), CISM Courses and Lectures, No. 374, Springer, Vienna, pp. 57- 100 (1997).
- Practical aspect of structural optimization, 2nd Edition Released 06/2015 Altair University.
- Practical aspect of finite element simulation, 3rd Edition Released 05/2015 Altair University.
- A. J. M. Ferreira, MATLAB Codes for Finite Element Analysis: Solids and Structures (Solid Mechanics and Its Applications) (2014)
 Vijay Jamariya
Vijay Jamariya