An Optimised Density Based Clustering Algorithm

An Optimised Density Based Clustering Algorithm

J. Hencil Peter
Department of Computer Science
St. Xavier’s College, Palayamkottai, India

A. Antonysamy
Department of Mathematics St. Xavier’s College, Kathmandu, Nepal

Abstract

The DBSCAN [1] algorithm is a popular algorithm in Data Mining field as it has the ability to mine the noiseless arbitrary shape Clusters in an elegant way. As the original DBSCAN algorithm uses the distance measures to compute the distance between objects, it consumes so much processing time and its computation complexity comes as $\mathrm{O}\left(\mathrm{N}^{2}\right)$. In this paper we have proposed a new algorithm to improve the performance of DBSCAN algorithm. The existing algorithms A Fast DBSCAN Algorithm[6] and Memory effect in DBSCAN algorithm[7] has been combined in the new solution to speed up the performance as well as improve the quality of the output. As the RegionQuery operation takes long time to process the objects, only few objects are considered for the expansion and the remaining missed border objects are handled differently during the cluster expansion. Eventually the performance analysis and the cluster output show that the proposed solution is better to the existing algorithms.

Keywords

Optimised DBSCAN, Density Cluster, Optimised RegionQuery, RegionQuery.

1. INTRODUCTION

Data mining is a fast growing field in which clustering plays a very important role. Clustering is the process of grouping a set of physical or abstract objects into classes of similar objects [2]. Among the many algorithms proposed in the clustering field, DBSCAN is one of the most popular algorithms due to its high quality of noiseless output clusters. As the original DBSCAN algorithm RegionQuery function is very expensive factor in terms of time, we have proposed a solution to minimize the RegionQuery function call to cover the maximum neighbours in an elegant way. The Fast DBSCAN Algorithm’s[6] seleted seed objects’ RegionQuery has been improved to give the better output, at the same time within less time using Memory effect in DBSCAN algorithm[7]. The remaining objects present in the border area have been examined separately during the cluster expansion which is not done in the Fast DBSCAN Algorithm. So the new algorithm is capable to give the better performance than the existing DBSCAN algorithms.

Rest of the paper is organised as follows. Section 2 gives the brief history about the related works in the same area. Section 3 gives the introduction of original DBSCAN and section 4 explains the proposed algorithm. After the new algorithm’s explanation, section 5 shows the Experimental Results and final section 6 presents the conclusion and future work associated with this algorithm.

2. RELATED WORK

The DBSCAN (Density Based Spatial Clustering of Application with Noise) [1] is the basic clustering algorithm to mine the clusters based on objects density. In this algorithm, first the number of objects present within the neighbour region (Eps) is computed. If the neighbour objects count is below the given threshold value, the object will be marked as NOISE. Otherwise
the new cluster will be formed from the core object by finding the group of density connected objects that are maximal w.r.t densityreachability.

The CHAMELEON [3] is a two phase algorithm. It generates a k-nearest graph in the first phase and hierarchical cluster algorithm has been used in the second phase to find the cluster by combining the sub clusters.

The OPTICS [4] algorithm adopts the original DBSCAN algorithm to deal with variance density clusters. This algorithm computes an ordering of the objects based on the reachability distance for representing the intrinsic hierarchical clustering structure. The Valleys in the plot indicate the clusters. But the input parameters $\xi$ is critical for identifying the valleys as $\xi$ clusters.

The DENCLUE [5] algorithm uses kernel density estimation. The result of density function gives the local density maxima value and this local density value is used to form the clusters. If the local density value is very small, the objects of clusters will be discarded as NOISE.

A Fast DBSCAN (FDBSCAN) Algorithm[6] has been invented to improve the speed of the original DBSCAN algorithm and the performance improvement has been achieved through considering only few selected representative objects belongs inside a core object’s neighbour region as seed objects for the further expansion. Hence this algorithm is faster than the basic version of DBSCAN algorithm and suffers with the loss of result accuracy.

The MEDBSCAN [7] algorithm has been proposed recently to improve the performance of DBSCAN algorithm, at the same time without loosing the result accuracy. In this algorithm totally three queues have been used, the first queue will store the neighbours of the core object which belong inside Eps distance, the second queue is used to store the neighbours of the core object which belong inside $2 *$ Eps distance and the third queue is the seeds queue which store the unhandled objects for further expansion. This algorithm guarantees some notable performance improvement if Eps value is not very sensitive.

Though the DBSCAN algorithm’s complexity can be reduced to $\mathrm{O}\left(\mathrm{N} * \log \mathrm{~N}\right)$ using some spatial trees, it is an extra effort to construct, organize the tree and the tree requires an additional memory to hold the objects. In this new algorithm we have achieved good performance with original computation complexity $\mathrm{O}\left(\mathrm{N}^{2}\right)$.

3. INTRODUCTION TO DBSCAN ALGORITHM

In the following definitions, a database D with set of points of k dimensional space $S$ has been used. As we need to find out the object neighbours which are exist/surrounded with in the given radius (Eps), Euclidean function dist (p, q) has been used, where p and q are the two objects. This function takes two objects and gives the distance between them.

Definition 1: Eps Neighbourhood of an object p
The Eps Neighbourhood of an object p is referred as NEps(p), defined as

$$\mathrm{NEps}(\mathrm{p})=\{\mathrm{q} \in \mathrm{D} \mid \operatorname{dist}(\mathrm{p}, \mathrm{q})<<\text { Eps }\}$$

Definition 2: Core Object Condition
An Object p is referred as core object, if the neighbour objects count $>=$ given threshold value (MinObjs).
i.e. $|\mathrm{NEps}(\mathrm{p})|>=\mathrm{MinObjs}$

Where MinObjs refers the minimum number of neighbour objects to satisfy the core object condition. In the above case, if p has neighbours which are exist within the Eps radius count is $>=$ MinObjs, p can be referred as core object.

Definition 3: Directly Density Reachable Object
An Object p is referred as directly density reachable from another object q w.r.t Eps and MinObjs if
$\mathrm{p} \in \mathrm{NEps}(\mathrm{q})$ and
$|\mathrm{NEps}(\mathrm{q})|>=\mathrm{MinObjs}$ (Core Object condition)
Definition 4: Density Reachable Object
An object p is referred as density reachable from another object q w.r.t Eps and MinObjs if there is a chain of objects p1,…,pn, $\mathrm{p} 1=\mathrm{q}, \mathrm{pn}=\mathrm{p}$ such that $\mathrm{pi}+1$ is directly density reachable from pi.

Definition 5: Density connected object
An Object p is density connected to another object q if there is an object o such that both, p and q are density reachable from o w.r.t Eps and MinObjs.

Definition 6: Cluster

A Cluster C is a non-empty subset of a Database D w.r.t Eps and MinObjs which satisfying the following conditions.

For every p and q , if $\mathrm{p} \in$ cluster C and q is density reachable from p w.r.t Eps and MinObjs then $\mathrm{q} \in \mathrm{C}$.
For every p and $\mathrm{q}, \mathrm{q} \in \mathrm{C} ; \mathrm{p}$ is density connected to q w.r.t Eps and MinObjs.

Definition 7: Noise

An object which doesn’t belong to any cluster is called noise.
The DBSCAN algorithm finds the Eps Neighbourhood of each object in a Database during the clustering process. Before the cluster expansion, if the algorithm finds any non core object, it will be marked as NOISE. With a core object, algorithm initiate a cluster and surrounding objects will be added into the queue for the further expansion. Each queue objects will be popped out and find the Eps neighbour objects for the popped out object. When the new object is a core object, all its neighbour objects will be assigned with the current cluster id and its unprocessed neighbour objects will be pushed into queue for further processing. This process will be repeated until there is no object in the queue for the further processing.

4. PROPOSED SOLUTION

A new algorithm has been proposed in this paper to overcome the problem of the performance issue which exists in the density based clustering algorithms. In this algorithm, number of RegionQuery call has been reduced as well as some RegionQuery calls speed has been improved. For reducing the RegionQuery
function calls, FDBSCAN Algorithm’s [3] selected representative objects as seed objects approach during the cluster expansion has been used in this solution and this approach has been proved theoretically using the following Lemmas 1 and 2. As the RegionQuery retrieve the neighbour objects which belong inside the Eps radius, Circle lemmas are given and which can be directly used in the RegionQuery optimization.

Lemma 1: Minimum number of identical circles required to cover the circumference of a circle with same radius which passes through the centres of other circles is three.

Proof: Let C and $\mathrm{C}_{1}$ be the identical circles of radius r with centre at O and $\mathrm{O}_{1}$ respectively. Assume the circle C passes through the centre $\mathrm{O}_{1}$ of the circle $\mathrm{C}_{1}$ and the circle $\mathrm{C}_{1}$ passes through the centre O of the circle C . Let the circles intersect at P and Q .

Figure 1 Two Identical Circles’ Intersection with respect to first circle’s Center Point.

Clearly, $\mathrm{OP}=\mathrm{OQ}=\mathrm{r} ; \mathrm{O}_{1} \mathrm{P}=\mathrm{O}_{1} \mathrm{Q}=\mathrm{r}$ and $\mathrm{OO}_{1}=\mathrm{r}$.
$\Delta \mathrm{O}_{1} \mathrm{OP}$ and $\Delta \mathrm{O}_{1} \mathrm{QO}$ are equilateral.

$$\begin{aligned} & \angle \mathrm{POO}_{1}=\angle \mathrm{QOO}_{1}=60^{\circ} \\ & \therefore \angle \mathrm{POQ}=\angle \mathrm{POO}_{1}+\angle \mathrm{QOO}_{1}=120^{\circ} \end{aligned}$$

Now length of arc $\mathrm{PO}_{1} \mathrm{Q}=\frac{120^{\circ}}{360^{\circ}} \times 2 \pi \mathrm{r} \quad=\frac{2 \pi \mathrm{r}}{3}$
$\frac{2 \pi \mathrm{r}}{3}$.
Thus arcual length 3 of the circumference of the given circle C is covered by $\mathrm{C}_{1}$. In order to cover the remaining part of the circumference of circle C , draw a circle $\mathrm{C}_{2}$ of same radius r with centre $\mathrm{O}_{2}$, passes through O and P . Let $\mathrm{C}_{2}$ intersect C at another point R (say).

Figure 2 Four Identical Circles intersection w.r.t first Circle’s center point.

Length of arc $\mathrm{PO}_{2} \mathrm{R}=\begin{array}{ll}\frac{2 \pi \mathrm{r}}{3} & \text { [proceeding as above] } \\ \frac{2 \pi \mathrm{r}}{3} & \end{array}$
i.e., arcual length $\quad 3$ of the circumference of the given circle C is covered by $\mathrm{C}_{2}$

$$\frac{4 \pi \mathrm{r}}{3}$$

Thus the circles $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ can able to cover only $\quad 3$ part of the circumference of the circle C. i.e., in order to cover the complete circumference of the circle C we are required to draw one more circle $\mathrm{C}_{3}$ passes through $\mathrm{O}, \mathrm{Q}$ and R with centre at $\mathrm{O}_{3}$ and radius r.

$$\frac{2 \pi \mathrm{r}}{3}$$

Length of arc $\mathrm{RO}_{3} \mathrm{Q}=\frac{2 \pi \mathrm{r}}{3}$
of $\operatorname{arc} \mathrm{RO}_{3} \mathrm{Q}=3 \times \frac{2 \pi \mathrm{r}}{3}=2 \pi \mathrm{r}$, which is the perimeter of the circumference of the circle C. Hence minimum three identical circles required to cover the circumference of a circle with same radius which passes through the centres of other circles.

Lemma 1 proves that the minimum requirement to cover the circumference of the center circle and these minimum circles selection is equivalent to the RegionQuery call in the DBSCAN algorithm. In the real scenario, three RegionQuery call is not sufficient to cover most the neighbours which exist in the center object’s neighbours when the objects in the dataset is distributed uniformly(assume the objects are distributed uniformly and the distance between an object and its neighbour is 1). Moreover these three RegionQuery function calls are not sufficient to cover immediate neighbours of the center object’s neighbours and this problem is explained below:

Figure 3 Missing immediate neighbour Objects.
Above picture shows that a circle (“Original Circle”) is been intersected by three other identical circles. Even though the three circles are covering the full circumference of the original circle, these three circles are not able to cover center circle’s immediate neighbours which are marked in red colour (p1, p2 and p3). i.e. even if the distance between the intersection point and the immediate neighbour point is 1 , above scenario can’t cover the all its immediate neighbours. So the Lemma 2 has been introduced to prove the minimum circles requirement to cover all the immediate neighbours.
Lemma 2: Four identical circles are sufficient to cover all the immediate neighbour objects of the original circle when the objects are distributed uniformly.

Figure 4 Minimum Circles to cover the immediate neighbours.

Proof:

Clearly, $\mathrm{O}_{3} \mathrm{OO}_{2} \mathrm{P}$ is a square of side r .

$$\therefore O P=\text { Diagonal of the square of side } \mathrm{r} \quad=\mathrm{r} \sqrt{2}$$

Distance $\mathrm{AP}=\mathrm{r} \sqrt{2}-\mathrm{r}=\sqrt{2}-1 \mathrm{r}=0.4142 \mathrm{r}$
Thus four circles are able to cover the objects which are at most 0.4142 r distance apart from the circumference of the original circle C.
So we need minimum four RegionQuery call to cover all the immediate neighbours of the center Object’s neighbours and this will cover $>80 \%$ of the neighbour objects of center object’s neighbours. This can be proved as follows:

Lemma 3: Four Identical Circles are sufficient to cover more than $80 \%$ of the neighbour objects of center circle when objects are distributed uniformly.

Proof:

Figure 5 Neighbours unreachable area.
Area of outer circle (with radius $2 \mathrm{r}$ ) $=\pi \mathbf{r}_{\mathrm{r}}^{\mathrm{T}}=4 \pi \mathrm{r}^{2}$
Area of the square PQRS (with side $2 \mathrm{r}$ ) $=\mathbf{r}_{\mathrm{r}}^{\mathrm{T}}=4 \mathrm{r}^{2}$

Total area of four semi circles (each with radius r) $=4 \times \frac{\pi \mathrm{r}^{2}}{2}=2 \pi \mathrm{r}^{2}$
Hence area of unmarked region

$$=4 \mathrm{r}^{2}+$$

$2 \pi \mathrm{r}^{2}$

$$\begin{aligned} \therefore \text { Area of marked region } & =4 \pi \mathrm{r}^{2}-\left(4 \mathrm{r}^{2}+2 \pi \mathrm{r}^{2}\right)=2 \pi \mathrm{r}^{2}-4 \mathrm{r}^{2} \\ & =2(\pi-2) \mathrm{r}^{2} \end{aligned}$$

Percentage of area in outer circle covered by the marked area $=$ $\frac{2(\pi-2) \mathrm{r}^{2}}{4 \pi \mathrm{r}^{2}} \times 100 \%$

$$=\left(\frac{\pi-2}{\pi}\right) \times 50 \%$$

Hence the area occupied by the marked region is $<20$ percentage.
So in the real time scenario we can conclude that if we select four seed objects for the cluster expansion from the center object’s neighbours we have the chances to ignore $\sim 20 \%$ of the objects which present in the border region and the previous FDBSCAN algorithm ignore these objects. In this solution, this problem has been rectified and all the border objects have been considered for the clustering operation.

To improve the performance of the algorithm, MEDBSCAN Algorithm [6] approach has been applied. So there are two types of Regionquery functions have been introduced in this algorithm namely, LongRegionQuery and ShortRegionQuery. First LongRegionQuery function will be called to get the region objects present in Eps neighbours as well as $2 *$ Eps neighbours surrounded by the given object, the Eps distance neighbours from the center object will be stored in the InnerRegionObjects queue and the objects which are greater than Eps and less than or equal to $2 *$ Eps distance from the center objects will be stored in OuterRegionObjects queue respectively. Later the selected seed objects present in the Eps neighbour region will be processed using the ShortRegionQuery function call. So the ShortRegionQuery function call will be always faster than the LongRegionQuery function as it needs to process only few objects which are present in the InnerRegionObjects as well as OuterRegionObjects and no need to process the entire objects present in the data set.

Another change in the proposed solution to improve the speed is modification of queue structure. i.e InnerRegionObjects and OuterRegionObjects queues are the combination of four sub queues.

RegionObjectsQueue
{
    TopRightQueue;
    RightBottomQueue;
    BottomLeftQueue;
    LeftTopQueue;
}

4.1 Proposed Queue Structure

So InnerRegionObjects and OuterRegionObjects queues will maintain the corresponding region objects internally in four queues. Following diagram shows each queue’s object storage areas.

Figure 6 RegionObjectsQueue’s storage area classification.
This type of separation helps to minimize the unwanted distance computation while processing the border objects. i.e. while processing OuterRegionObjects queue’s unprocessed objects, we can consider only the adjacent portion of the InnerRegionObjects queue’s objects and other non adjacent portions objects can be ignored. This concept has been explained as follows.

4.2 Neighbour computation Ignore Case

Let ’ O ’ is an Outer Circle with radius $2 r$ and ’ I ’ is an inner circle with radius $r$. Both of these circles are sharing the same Center point ’ C ’ and these two circles are equally divided into four parts as shown in the below picture (to perform the RegionQuery operation).

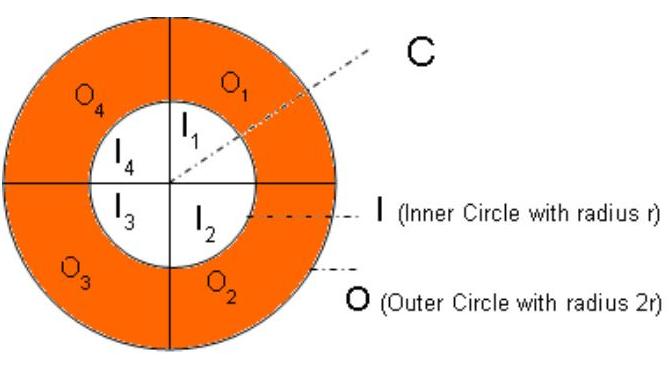
Figure 7 Inner and Outer Region Objects.
Here the inner circle objects’ neighbour objects are present in the outer circle’s marked area (with brown colour) and the inner circle itself. Now we can confirm that any object present in the inner circle’s any one of the quarter area ( $1_{1}$ OR $1_{2}$ OR $1_{3}$ OR $1_{4}$ ), will have its neighbour(s) in the 3 of the adjacent quarter part of the outer circle and the inner circle itself (four quarter parts). Thus we can ignore the outer circle’s non adjacent quarter part from the unnecessary computation.
(e.g)

Figure 8 Availability of Neighbour Objects in the Circle’s Portion.

In the above diagram Inner Circle’s $\mathrm{I}_{3}$ quarter portion has been considered for the neighbour computation. The object present in the $\mathrm{I}_{3}$ quarter portion will have its neighbours in $\mathrm{O}_{4}, \mathrm{O}_{5}, \mathrm{O}_{2}$ and the Inner circle itself ( $\mathrm{I}_{1}, \mathrm{I}_{2}, \mathrm{I}_{3}$ and $\mathrm{I}_{4}$ ), but not in $\mathrm{O}_{1}$ portion. i.e. Maximum r distance is the valid distance for neighbour computation and $\mathrm{I}_{3}$ 's object require minimum $\mathrm{r}+1$ distance to reach another object which is present in the $\mathrm{O}_{1}$ portion and this condition is not possible (Invalid condition has been shown in the diagram in red colour). Similarly while processing the border objects present in the OuterRegion, only the adjacent quarter portion of inner region objects are enough for the computation to know whether it is density reachable to any of the objects present in the InnerRegionObjects.

This is another optimization done in the new algorithm to speed up the computation as well as improve the accuracy of output. In the FDBSCAN algorithm, chances of missing the core objects as well as border objects are applicable and in this new approach all the border objects have been covered. Also it is proved that the core objects loss is very rare case and the new solution is better in most of the cases in the real time scenario.

4.3 Algorithm

1. Read D, Eps and MinObjs.
2. Initialize all objects Cluster ID field as UNCLASSIFIED.
3. For each UNCLASSIFIED object o $\in \mathrm{D}$
4. Call LongRegionQuery function with D, Eps and o parameters to be obtain InnerRegionObjects and OuterRegionObjects.
5. IF o is a core object Then
6. Get the ClusterID for the new Cluster.
7. Select four UNCLASSIFIED objects from the

InnterRegionObjects’ TopRight, RightBottom, BottomLeft and LeftTop Queues each for the further cluster expansion and push the selected objects to FourObjectsQueue. The selected objects should have the max distance from the center object o.
8. Assign ClusterID to all the UNCLASSIFIED and NOISE type Objects present in the InnerRegionObjects.
9. For each object $\mathrm{T} \in$ FourObjectsQueue
10. Call ShortRegionQuery function with InnerRegionObjects, OuterRegionObjects, Eps and Object T to obtain the ShortRegionObjects.
11. Select four UNCLASSIFIED objects from the ShortRegionObjects’ TopRight, RightBottom,

BottomLeft and LeftTop Queues for the further cluster expansion. The selected Objects should have the max distance from the center object T. Push the selected objects to SeedQueue for the further processing.
12. Assign ClusterID to all the UNCLASSIFIED and NOISE type Objects present in the ShortRegionObjects.
13. End For
14. Remove the clustered objects from the OuterRegionObjects and process the remaining (UNCLASSIFIED and NOISE type) Objects to know if any one of the InnerRegionObjects neighbour present in the UNCLASSIFIED and NOISE type OuterRegionObjects. i.e if any remaining objects present in the OuterRegionObjects is density reachable from the center object o’s neighbour, assign ClusterID to the Object.
15. Pop the objects s from SeedQueue, Repeat the steps from 4-14 and until the SeedQueue is Empty. For all the above steps replace the object o with SeedQueue Object s wherever it is applicable.
16. Else
17. Mark o as NOISE
18. End If
19. End For

This algorithm read the same input as like original DBSCAN and all the objects are initialized as UNCLASSIFIED in the beginning. Afterwards all the UNCLASSIFIED objects are processed one by one. So the algorithm starts with LongRegionQuery function call to obtain the Neighbour objects (InnerRegionobjects and OuterRegionObjects) and the cluster expansion will happen only if the current object is a core object, otherwise the current object will be market as NOISE. During the cluster expansion, the new Cluster ID will get created and four UNCLASSIFIED objects are selected from the InnerRegionobjects’ four queues each and these objects should have the maximum distance from the center object. After assigning the Cluster ID to all the Objects present in the InnerRegionObjects queue, the selected four objects will be processed. Here the four objects are the maximum count and if there is no UNCLASSIFIED object present in one or more specific queues, the selected objects count will be less than 4. For processing these objects, ShortRegionQuery has been used and each ShorRegionQuery operation, maximum four seed objects will be selected which meets the above condition and pushed into seed queue for the further cluster expansion. The ShortRegionQuery takes the return array objects of LongRegionQuery function and will not process the whole Data set in the subsequent iteration. Thus the performance improvement has been guaranteed when the Eps value is reasonably insensitive. The Cluster ID will be assigned to the ShortRegionQuery’s output objects if the object is either UNCLASSIFIED or NOISE. Now the remaining UNCLASSIFIED or NOISE type objects present in the OuterRegionObjects queue is processed and which uses the “Neighbour computation Ignore Case” computation approach to minimize the computation and speed up the performance. After repeating these steps as mentioned in the algorithm and when the SeedQueue become empty, the current cluster expansion will stop and the control moves to process the next object UNCLASSIFIED type object using the parent for loop. The whole clustering process will be over once the main loop visits the entire N objects present in the data set.

5. PERFORMANCE ANALYSIS

The basic DBSCAN, Fast DBSCAN and proposed Optimized DBSCAM algorithms are implemented in Visual C++ (2008) on Windows Vista OS and tested using two dimensional Dataset. To know the real performance difference achieved in the new algorithm, we haven’t used any additional data structures (like spatial tree) to improve the performance. These algorithms are tested using two dimensional synthetic dataset and the performance results are shown below.

Table 1 Running time of Algorithms in Seconds

	DBSCAN		FDBSCAN		ODBSCAN
300	0.096	0	0.078	3	0.064	0
500	0.274	0	0.185	11	0.128	1
700	0.483	0	0.256	26	0.177	3
1200	1.024	0	0.581	34	0.345	7
2500	4.850	0	1.021	77	0.662	13

Above table shows that the new algorithm’s performance is better to the existing algorithms in terms of computation time and the new algorithm has small number of object loss than the Fast DBSCAN algorithm.

6. CONCLUSION AND FUTURE WORK

In this paper we have proposed ODBSCAN algorithm to improve the performance with less amount of object loss. In this new algorithm FDBSCAN and MEDBSCAN algorithms approach has been used to improve the performance. Also some new techniques have been introduced to minimize the distance computation during the RegionQuery function call. Eventually the performance analysis and the output shows that the newly proposed ODBSCAN algorithm gives better output, at the same time with good performance.
In this algorithm, all the border objects have been considered for the clustering process. But there are few possibilities to miss the core objects and which causes some loss of objects. Though the new algorithm gives better result than the previous FDBSCAN algorithm, this problem needs to be resolved in the further work to give the accurate result with same performance.

7. REFERENCES

[1] Ester M., Kriegel H.-P., Sander J., and Xu X. (1996) “A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise” In Proceedings of the $2^{\text {nd }}$ International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland: Oregon, pp. 226-231
[2] J. Han and M. Kamber, Data Mining Concepts and Techniques. Morgan Kaufman, 2006.
[3] G. Karypis, E. H. Han, and V. Kumar, “CHAMELEON: A hierarchical clustering algorithm using dynamic modeling,” Computer, vol. 32, no. 8, pp. 68-75, 1999.
[4] M. Ankerst, M. Breunig, H. P. Kriegel, and J. Sander, “OPTICS: Ordering Objects to Identify the Clustering Structure, Proc. ACM SIGMOD,” in International Conference on Management of Data, 1999, pp. 49-60.
[5] A. Hinneburg and D. Keim, “An efficient approach to clustering in large multimedia data sets with noise,” in 4th International Conference on Knowledge Discovery and Data Mining, 1998, pp. 58-65.
[6] SHOU Shui-geng, ZHOU Ao-ying JIN Wen, FAN Ye and QIAN Wei-ning.(2000) “A Fast DBSCAN Algorithm” Journal of Software: 735-744.
[7] Li Jian; Yu Wei; Yan Bao-Ping; , “Memory effect in DBSCAN algorithm,” Computer Science & Education, 2009. ICCSE 199. 4th International Conference on , vol., no., pp.31-36, 25-28 July 2009.

AUTHOR PROFILES

J. Hencil Peter is Research Scholar, St. Xavier’s College (Autonomous), Palayamkottai, Tirunelveli, India. He earned his MCA (Master of Computer Applications) degree from Manonmaniam Sundaranar University, Tirunelveli. Now he is doing Ph.D in Computer Applications and Mathematics (Interdisciplinary) at Manonmaniam Sundranar University, Tirunelveli. His interested research area is algorithms inventions in data mining.

Dr. A. Antonysamy is Principal of St. Xavier’s College, Kathmandu, Nepal. He completed his Ph.D in Mathematics for the research on “An algorithmic study of some classes of intersection graphs”. He has guided and guiding many research students in Computer Science and Mathematics. He has published many research papers in national and international journals. He has organized Seminars and Conferences in state and national level.