Academia.eduAcademia.edu

Outline

Title
Abstract
Figures
Introduction
Methodology
Results and Discussion
Conclusion
References
All Topics
Computer Science
Software

Kolam Simulation using Angles at Lattice Points

Profile image of Shailaja D SharmaShailaja D Sharma

2023, arXiv (Cornell University)

Abstract

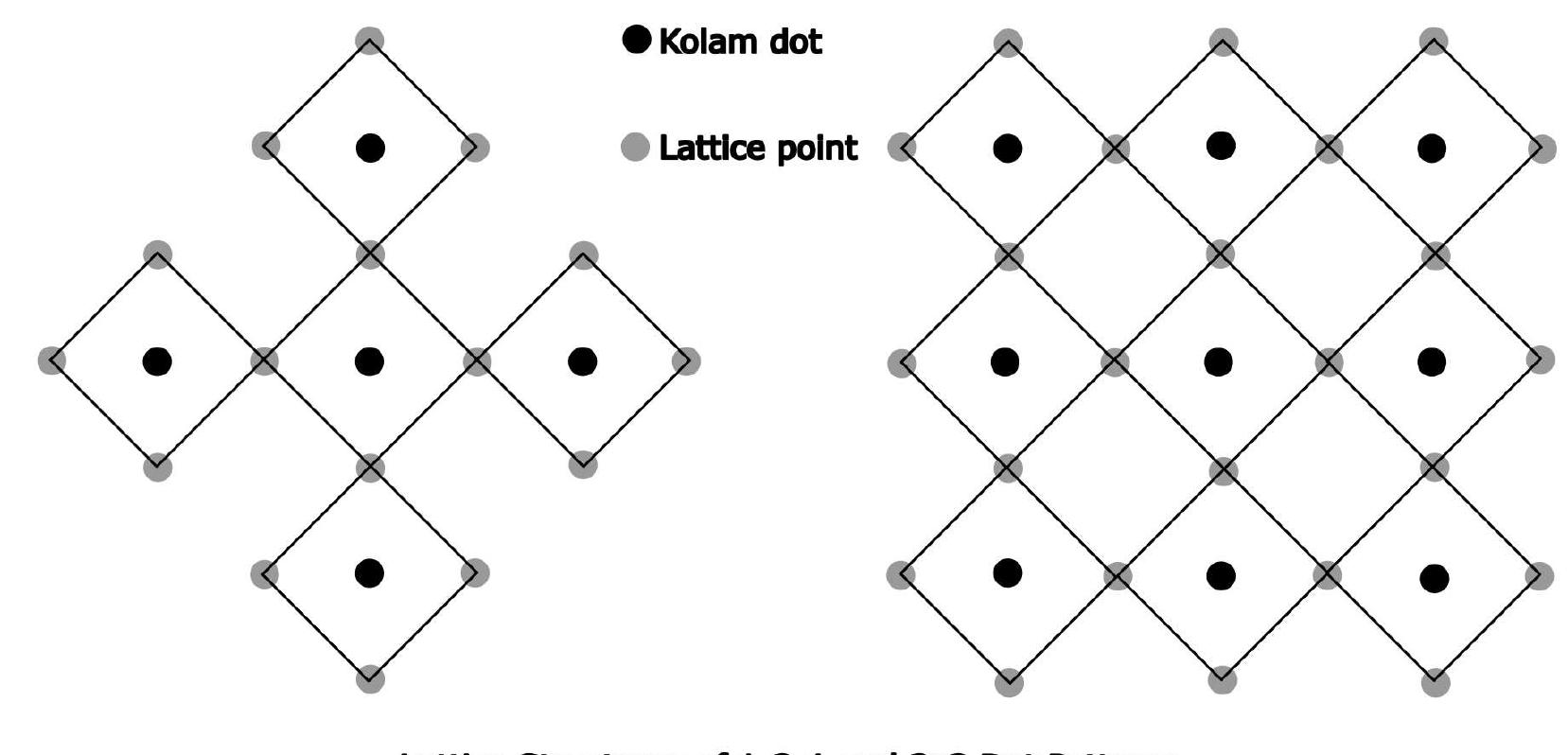
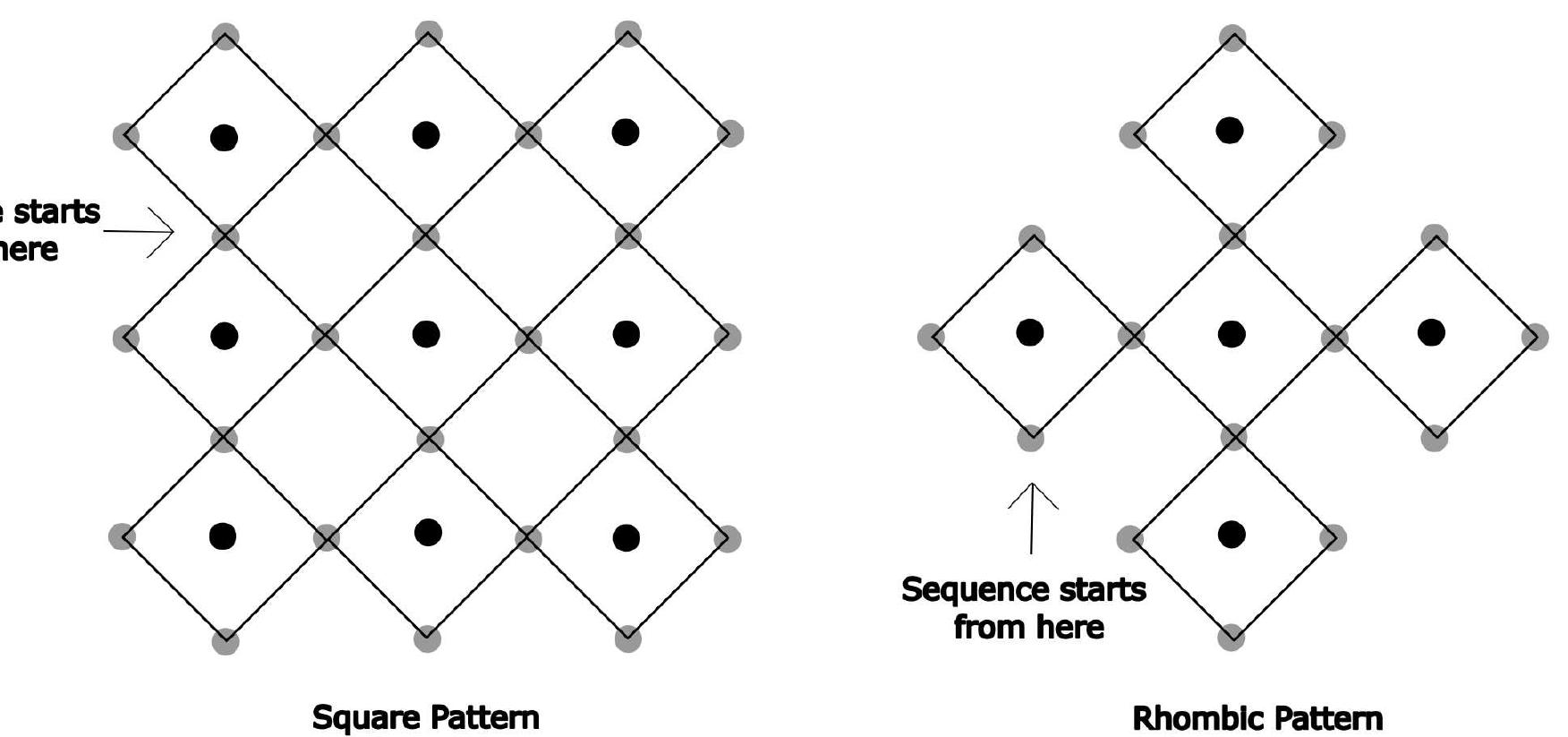
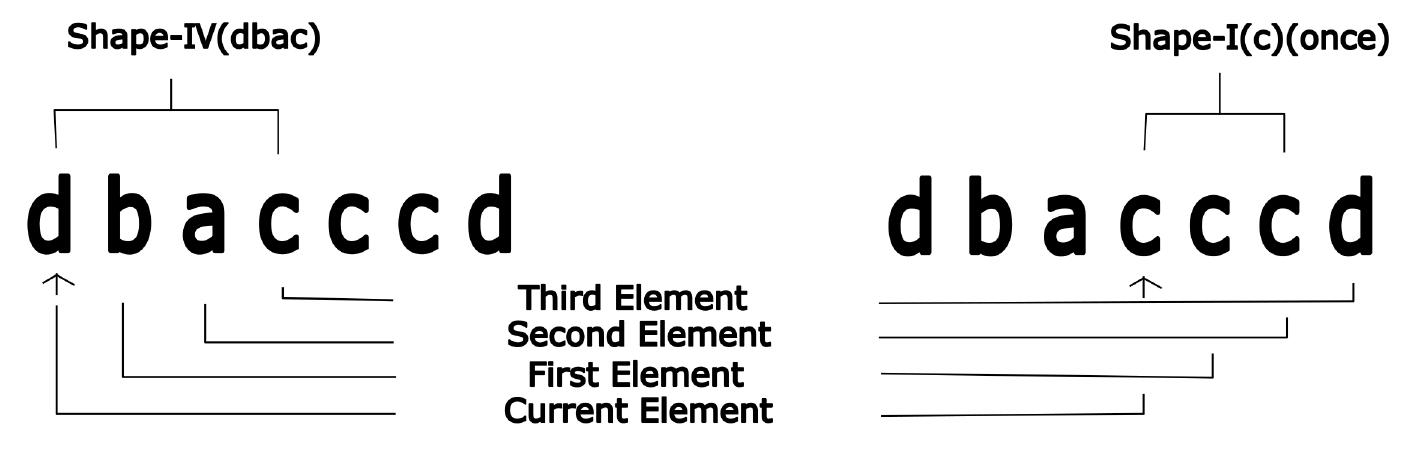
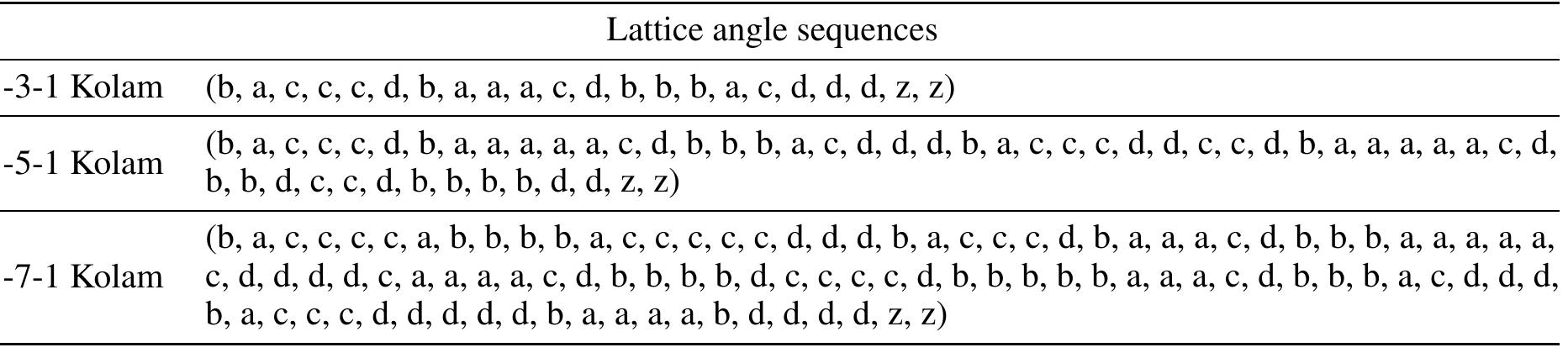
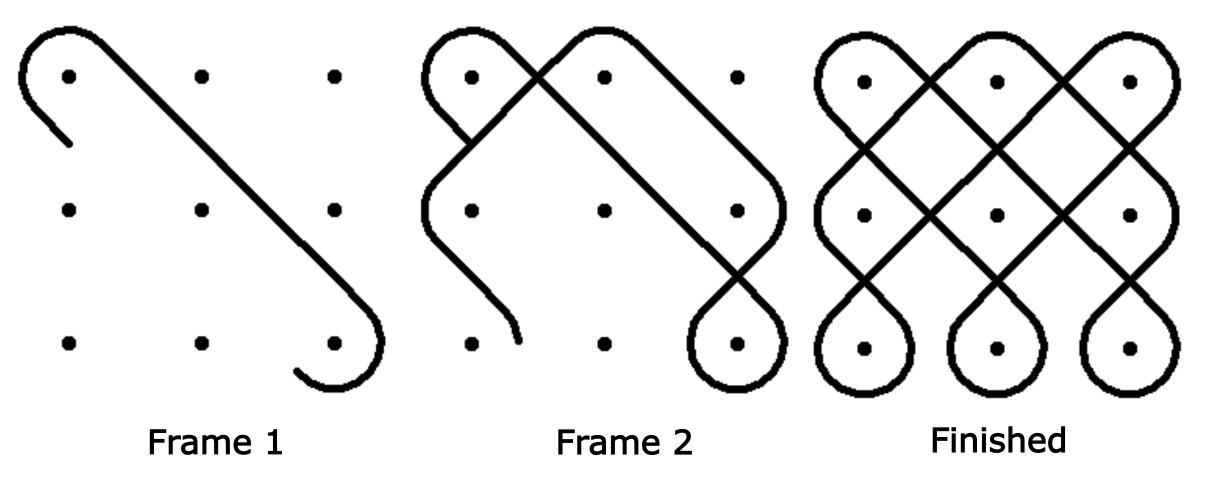
Kolam is a ritual art form practised by people in South India and consists of rule-bound geometric patterns of dots and lines. Single loop Kolams are mathematical closed loop patterns drawn over a grid of dots and conforming to certain heuristics. In this work, we propose a novel encoding scheme where we map the angular movements of Kolam at lattice points into sequences containing 4 distinct symbols. This is then used to simulate single loop Kolam procedure via turtle moves in accordance with the desired angular direction at specific points. We thus obtain sequential codes for Kolams, unique up to cyclic permutations. We specify the requirements for the algorithm and indicate the general methodology. We demonstrate a sample of Kolams using our algorithm with a software implementation in Python.

Figures (38)
Figure 1: Deciding where to go while drawing a Kolam - Part 1.
Figure 1: Deciding where to go while drawing a Kolam - Part 1.
Figure 2: Deciding where to go while drawing Kolam - Part 2.
Figure 2: Deciding where to go while drawing Kolam - Part 2.
Figure 5: Lattice structures imposed on 1 — 3 — 1 and 3 x 3 dot patterns. Figure 4: Cardinal directions of a Kolam dot and intercardinal directions of a lattice point.
Figure 5: Lattice structures imposed on 1 — 3 — 1 and 3 x 3 dot patterns. Figure 4: Cardinal directions of a Kolam dot and intercardinal directions of a lattice point.
Figure 3: A square unit cell imposed on a Kolam dot.
Figure 3: A square unit cell imposed on a Kolam dot.
Table 1: Coding lattice angles
Table 1: Coding lattice angles
Figure 7: Direction of a point with respect to its predecessor point. Figure 6: Direction of point B from point A.
Figure 7: Direction of a point with respect to its predecessor point. Figure 6: Direction of point B from point A.
Figure 8: Convention for sequence start-point of square and rhombic Kolams.
Figure 8: Convention for sequence start-point of square and rhombic Kolams.
‘igure 9: A 1 — 3 — 1 Kolam with angle changes while drawing.
‘igure 9: A 1 — 3 — 1 Kolam with angle changes while drawing.
Figure 10: Angle changes in Fig. 9 replaced with their corresponding symbols.
Figure 10: Angle changes in Fig. 9 replaced with their corresponding symbols.
Figure 11: Shapes involved in single loop Kolams.
Figure 11: Shapes involved in single loop Kolams.
Figure 12: “0 changes in symbol” shapes. Figure 13: “1 change in symbol” shapes in vertical direction.
Figure 12: “0 changes in symbol” shapes. Figure 13: “1 change in symbol” shapes in vertical direction.
conditions, the loop will be terminated after iterating through these z’s. The Kolam drawing will be finished. For shape-III and shape-IV, even if there are no z’s, no problem will arise. For example, if the sequence ends with ‘dcab’, the shape-IV (dcab) will be drawn and the loop will be terminated without any errors. The Kolam drawing will be finished. But if z’s are not added, it raises an error or selects a wrong shape when the final shape is either shape-I or shape-II. For example, if the sequence ends with ‘aab’, there is no change from a—a and this is a shape-I (a) pattern but there is a change from a—+b. It is the first condition with no shape specified in section 6. Now ‘a’ becomes the current element. There is a change from a—+b and it needs to take second step to determine the shape. As there is no element after ‘b’, it will raise an error. To avoid these errors and discrepancies and to encode all Kolams in a standard way, we add z’s in the end of a Kolam sequence. The loop will always be terminated after iterating through these z’s.
conditions, the loop will be terminated after iterating through these z’s. The Kolam drawing will be finished. For shape-III and shape-IV, even if there are no z’s, no problem will arise. For example, if the sequence ends with ‘dcab’, the shape-IV (dcab) will be drawn and the loop will be terminated without any errors. The Kolam drawing will be finished. But if z’s are not added, it raises an error or selects a wrong shape when the final shape is either shape-I or shape-II. For example, if the sequence ends with ‘aab’, there is no change from a—a and this is a shape-I (a) pattern but there is a change from a—+b. It is the first condition with no shape specified in section 6. Now ‘a’ becomes the current element. There is a change from a—+b and it needs to take second step to determine the shape. As there is no element after ‘b’, it will raise an error. To avoid these errors and discrepancies and to encode all Kolams in a standard way, we add z’s in the end of a Kolam sequence. The loop will always be terminated after iterating through these z’s.
Figure 14: “1 change in symbol” shapes in horizontal direction.
Figure 14: “1 change in symbol” shapes in horizontal direction.
Figure 15: “2 changes in symbol” shapes in clockwise direction.
Figure 15: “2 changes in symbol” shapes in clockwise direction.
Figure 16: “2 changes in symbol” shapes in anti-clockwise direction.
Figure 16: “2 changes in symbol” shapes in anti-clockwise direction.
Figure 17: “3 changes in symbol” shapes in anti-clockwise direction.
Figure 17: “3 changes in symbol” shapes in anti-clockwise direction.
Figure 18: “3 changes in symbol” shapes in clockwise direction.
Figure 18: “3 changes in symbol” shapes in clockwise direction.
Figure 19: Iterating through the sequence: an example. 6 Kolam Simulation Algorithm
Figure 19: Iterating through the sequence: an example. 6 Kolam Simulation Algorithm
We can also use the sequence in a cyclic iteration without z’s and adding ‘b’ in the third position from the last of the sequence. In this case it will draw the Kolam infinite times without stopping. The output of this Kolam is given in Figure 29.
We can also use the sequence in a cyclic iteration without z’s and adding ‘b’ in the third position from the last of the sequence. In this case it will draw the Kolam infinite times without stopping. The output of this Kolam is given in Figure 29.
Table 2: Navagraha Kolams and corresponding digital sequences
Table 2: Navagraha Kolams and corresponding digital sequences
Table 3: Rhombic Kolams and corresponding digital sequences
Table 3: Rhombic Kolams and corresponding digital sequences
Figure 21: Navagraha (3 x 3 square) Kolam 2.
Figure 21: Navagraha (3 x 3 square) Kolam 2.
Figure 22: Navagraha (3 x 3 square) Kolam 3.
Figure 22: Navagraha (3 x 3 square) Kolam 3.
Figure 26: Navagraha (3 x 3 square) Kolam 7. Figure 25: Navagraha (3 x 3 square) Kolam 6.
Figure 26: Navagraha (3 x 3 square) Kolam 7. Figure 25: Navagraha (3 x 3 square) Kolam 6.
Figure 24: Navagraha (3 x 3 square) Kolam 5. Figure 23: Navagraha (3 x 3 square) Kolam 4.
Figure 24: Navagraha (3 x 3 square) Kolam 5. Figure 23: Navagraha (3 x 3 square) Kolam 4.
Figure 30: A 1 — 5 — 1 rhombic Kolam. Figure 29: A 1 — 3 — 1 rhombic Kolam.
Figure 30: A 1 — 5 — 1 rhombic Kolam. Figure 29: A 1 — 3 — 1 rhombic Kolam.
Figure 28: Navagraha (3 x 3 square) Kolam 9.
Figure 28: Navagraha (3 x 3 square) Kolam 9.
Figure 27: Navagraha (3 x 3 square) Kolam 8.
Figure 27: Navagraha (3 x 3 square) Kolam 8.
Figure 31: A 1 — 7 — 1 rhombic Kolam.
Figure 31: A 1 — 7 — 1 rhombic Kolam.

Related papers

The Kolam Tradition A tradition of figure-drawing in southern India expresses mathematical ideas and has attracted the attention of computer science
Tarak Halder

American scientist, 2002

The kolam tradition of Tamil Nadu has persisted for hundreds of years and remains a common practice among women in cities as well as in rural areas, among those who are university-educated as well as those less schooled. In recent years, instead of rice, ...

View PDFchevron_right
Normalised grid/motif based patterns-Islamic geometric patterns
Ebad Banissi

Proceedings. 1997 IEEE Conference on Information Visualization (Cat. No.97TB100165)

The studies of Isiamic Geometric Patterns (IGP) show that the methods of generation is based on a set of classical gridding systenzr. They are hierarchical and primarily based on the sacred geometrical primitives (triangle. square and circle). With such patterns, symmetries are as visible as the forms themselves. They signify an obtlous secondary meaning that is so often referred, in the sacred and religious texts, to as a higher order of significance. Based on the classical grid system, normalised grid-based patterns proposes a neu' language of design with a further aids of symmetries that holds these forms so robustly. It takes away their hierarchy by replacing it with a less tangible forms that are bounded by shear balance of symmetries. An underlined question for the reader is "Are we disturbing the semantics of these patterns, the meaning that ha1.e been portrayed by architect, tile designers anal visualists for a long time though their visual forms?"

View PDFchevron_right
Generating Islamic Quasi-Periodic Patterns
rachid benslimane

Journal on Computing and Cultural Heritage, 2018

The discovery of quasi-crystals has led to a great debate about their unusual structure. The big surprise is that these structures were found in Islamic art several centuries ago. This latest discovery drew the attention of scientists to propose several approaches for the comprehension of these structures by analyzing several quasi-periodic patterns spread around the Islamic world. In this article, we propose a systematic method for generating new quasi-periodic patterns inspired by existing Islamic historical patterns. The method builds Islamic quasi-periodic patterns based on a quasi-periodic tiling and a few intuitive parameters. Given a quasi-periodic tiling, the method divides its tiles (rhombs) into symmetric right triangles and constructs their template motifs. The construction of these template motifs is achieved by a systematic and well-organized process. The content of the tiles is obtained by applying mirror reflections to the constructed template motifs. Finally, the pat...

View PDFchevron_right
Circle digitization and cellular automata
Laure Tougne

Lecture Notes in Computer Science, 1996

The article studies the discrete circles with the help of cellular automata. It is shown that if we consider a discrete circle as a succession of horizontal, diagonal and vertical segments which lean on a beam of parabolas, we can describe it by local properties and so, construct it by cellular automata. In fact, two algorithms are examined. The first one localizes the intersections between a given real circle and the grid. The second one constructs a well-known discrete circle: the arithmetical circle.

View PDFchevron_right
Extended pasting scheme for kolam pattern generation
Robinson Thamburaj

Forma, 2007

The theory of "Formal Languages" had been applied successfully to study the aspect of generating patterns of the kolam folk designs. In this paper a new picture generating method by the use of pasting of tiles is presented. The generating model "Pasting Scheme" and its variant "Extended Pasting Scheme" are shown to generate patterns including kolams of kambi and non-kambi types and tessellations as well.

View PDFchevron_right
Pattern Formation Using Cellular Automata and L-Systems: A Case Study in Producing Islamic Patterns
Seyyed Amir Hadi Minoofam

Emergence, Complexity and Computation, 2014

The science of pattern formation deals with the visible, (statistically) orderly outcomes of self-organization and the common principles behind similar patterns in nature. Cell pattern formation has an important role in both artificial and natural development. Different methods have been utilized for pattern formation such as geometrical, Cellular Automata (CAs), and L-Systems. In this chapter, we concentrate our aim on introducing the role of CAs and L-Systems in pattern formation and how to extract optimum rules in terms of numbers and functionality for this aim. Because a few works have been reported in the field of script generation, we take generating Ma'qeli script and Holy words patterns, as a case study, in hand. Results of this study show the superiority of the proposed method in comparison with geometrical and fractal approaches in case of the time complexity in word production, simplicity of extracted rules, and possible reusability of the CAs rules in generating other script patterns in other languages. Moreover, the proposed method is shape-resistance, which can be less seen in fractals and geometrical based pattern formation.

View PDFchevron_right
Fermats Spiral Mandalas
Robert J. Krawczyk

This paper explores Fermat's Spiral as a method to create circular point figures. It traces previous research into the variety of patterns created by the Fermat's Spiral based on a variety different angle intervals and number of points that control the scale of the figure and the packing of the spiral. Finally, a procedure of combining a series of spirals is proposed to form a mandala.

View PDFchevron_right
Digitalization of Batik Parang Pattern Using Turtle Graphics
Goldfrid Thomas

Prosiding ISBI Bandung, 2021

Salah satu warisan budaya Indonesia yang masih berkembang saat ini adalah batik. Kekayaan khasanah batik dapat dilihat dari berbagai motif batik yang ada di Indonesia. Batik Parang sebagai adalah motif batik tertua yang banyak ditemui di kota Surakarta dan sekitarnya. Motif batik Parang dikenal dan berkembang sejak zaman keraton Mataram Surakarta. Batik Parang sering digunakan pada acara-acara pembukaan pada zaman kerajaan. Motif batik Parang didominasi warna coklat gelap dan desain motif ini mengikuti garis diagonal dengan ukiran di setiap batas garisnya. Nama "Parang" berasal dari kata "Pereng" yang artinya "Lereng". Sesuai dengan arti katanya maka motif batik Parang berbentuk seperti lereng menurun dari posisi tempat yang tinggi ke posisi tempat yang lebih rendah secara diagonal. Motif batik Parang pada penelitian di sini akan didokumentasikan dalam bentuk program sehingga dapat disimpan dalam bentuk digital. Metode yang digunakan pada pembuatan motif batik parang adalah metode turtle graphics. Metode Turtle graphics dilandasi dengan gerak kura-kura yang dapat bergerak maju, berputar ke kanan, atau berputar ke kiri. Dengan metode yang sederhana ini digabungkan dengan perhitungan matematika, maka dibentuk garis-garis yang menjadi tepian dari motif batik, sehingga dengan mengatur arah gerak kura-kura maka motif batik Parang dapat dibentuk dengan baik. Pada penelitian ini, telah dirancang suatu program untuk membentuk motif batik Parang, dengan dokumentasi dalam bentuk digital diharapkan kelestarian dari seni budaya batik akan dapat abadi dan terus berkembang.

View PDFchevron_right
The Beauty, Dynamics, and Design of String-Patterns in Folk Arts
Shojiro Nagata

2007

This special issue focuses on an interdisciplinary discussion and exchange of information concerning scientific and artistic issues in traditional cultural, ethnological, and ritual art patterns throughout the world. Folk patterns include pictures or visual designs for textile, clothes, decorations, painting, furniture and other ornamental works for decorating or representing stories. For example, there are patterns of Japanese traditional dress (Kimono) called Shippo etc., and arabesque design, or closed string patterns such as floor painting (e.g. Kolam, Tamil Nadu, South India), Celtic knot design (Europe), sand painting (Sona, Central Africa or Nitus, Vanuatu, South Pacific Oceania) or, Asian knot (Olzii-hee, Mongolian Lucky knot, various types of Chinese and Korean knots, or Mizuhiki, Japanese knot, e.g. Takara), etc. Most of designs of the traditional patterns have geometric, periodical, cyclic, symmetrical, or recursive properties that possess rich religious or aesthetic features as well as mathematical or scientific features. These string and knot patterns have some unsolvedproblems, different from the Eulerian Cycle, which are now addressed as topics in knot/link theory in mathematics. The folk designs have been discussed recently not only as natural science, but also as anthropology or ecocriticism representing aspects of sprits or symbols of the cultures and their lands [Nagarajan], or as ethomathematics. For example, we perceive the universal flow/sprit in an infinite stroke pattern, or a return to life/resurrection in an endless-cycle pattern even in the present time. Pioneers were Prof. Profs Mr. and Mrs. Siromoney in Tamil Nadu, and Gerdes in Angola, Africa. Gerdes has discussed some common mathematical features from similar folk arts of different cultures [Gerdes]. Mathematical/graphical structures have been analyzed from the standpoint of chord diagrams [Jablan and Sazdanovic], knot theory [Ishimoto], numeric and linear diagram [Yanagisawa and Nagata], and then based on knowledge of how to draw/create such patterns with P Systems [Subramanian et al.], pasting schemes [Robinson], or hierarchical systems [Kishimoto and Natori], knot curves [Morita], and digitizing patterns [Nagata]. Some folk designs stimulate us to imagine their patterns expanded into the three dimensional space [Oka and Kawamoto]. Perhaps they will help advance understanding of other scientific fields, for example biological molecular structures (e g. DNA) in future. One article discusses representation of natural phenomena, such as water flow or plants, drawn in folk art patterns [Takaki and Ueda]. These papers also discuss beauty as a factor of aesthetic appeal that comes from patterns; e.g. symmetry, periodicity, or perception of an underlying algorithm that establishes the relationships among different regions. Given of a few simple elements we can generate a huge number of patterns, only a few of these of which are special forms of symmetry etc., and have low entropy (of rare proportion)/rich meaning. The unique pattern of the swastika is rotationally-symmetric, representing meaningfully the sunbeams and dynamics of this radiation, and then mysteriousness. Even stationary patterns may make us feel dynamics in them, and we can easily get them in tracing animated images of a Kolam/Knot patterns

View PDFchevron_right
Geometric Patterns Geometric Patterns
Pure Cube
View PDFchevron_right

References (9)

  1. Marcia Ascher. The kolam tradition. American Scientist, 90(1):56-63, 2002.
  2. Akhilesh Kumar and Shailaja D Sharma. Survey of computational methods in kolam. Paper presented at HOMI Young Scholars' Conference, IIT Gandhinagar, February 2021.
  3. Gift Siromoney, Rani Siromoney, and Kamala Krithivasan. Array grammars and kolam. Computer Graphics and Image Processing, 3(1):63-82, 1974.
  4. Gift Siromoney, Rani Siromoney, and Kamala Krithivasan. Picture languages with array rewriting rules. Informa- tion and Control, 22(5):447-470, 1973.
  5. Kiwamu Yanagisawa and Shojiro Nagata. Fundamental study on design system of kolam pattern. Bulletin of the Society for Science on Form, 21:133-134, 2007.
  6. Shojiro Nagata. Traditional kolam patterns: Formation, symmetry and fractal nature. In The Computation Meme: Computational Thinking in the Indic Tradition, K Gopinath and Shailaja D Sharma (Eds). IISc Press, Bangalore, (forthcoming) 2023.
  7. Aristid Lindenmayer. Mathematical models for cellular interactions in development i. filaments with one-sided inputs. Journal of Theoretical Biology, 18(3):280-299, 1968.
  8. Shojiro Nagata. How many loops kolam loop pattern consists of. Forma, January 2015.
  9. John Layard. Labyrinth ritual in south india: Threshold and tattoo designs. Folklore, 48(2):115-182, 1937.

Related papers

Mandala Art Creator: Art with Python Turtle Graphics
Anuradha Phadke

Deleted Journal, 2024

This work explores the use of Python Turtle graphics as a tool for designing art with programming concepts in creative ways. Turtle graphics is an easy and entertaining approach for learners to visualize and play with code in an artistic manner. The paper explains "Mandala Art Creator"; a Python program to generate a random or customized Mandala Art using the Turtle graphics module and its implementation in the textile industry. In Mandala Art Creator the user is prompted to provide their name and choose between two options: random configuration and personalized configuration. The computer's algorithm determines colors and angles for the Mandala Art on its own in random mode. The user can customize the Mandala Art experience in custom mode by specifying colors and rotation degrees.

View PDFchevron_right
Computer Graphics for Generating Islamic Geometric Periodic and Quasi-periodic Patterns
Zouhair OUAZENE

2019 International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), 2019

We present a simple method for constructing patterns of Islamic geometric art. The method allows creating a parameterized set of motifs within a fundamental region of a periodic pattern. The constructed template motif will undergo the inner symmetries of a chosen symmetry group to obtain the content of the unit cell. The whole pattern is obtained by applying several linearly independent translations to the generated unit motif. We show how this method can be adapted to construct Islamic quasi-periodic patterns.

View PDFchevron_right
Transformation Matrices in Generation of Circular Patterns
Ah Choo Koo

Jurnal Teknologi, 2015

This paper aims to explore the generation of circular patterns based on transformation matrix. The idea proposed here is to first design a fundamental pattern, known as ‘seed’. This is then followed by applying the transformation matrix to arrange the fundamental pattern to form a circular pattern. The transformation matrix can be applied once or applied iteratively. By assigning different values to the parameters involved, the patterns produced act in an interesting and appealing way. The proposed method contributes to a simple and efficient framework in computational generation of endless circular patterns.

View PDFchevron_right
Fabricating Algorithmic Art
Ellen Harlizius-Klück

2018

View PDFchevron_right
New Approach to Construct a New Islamic Geometric Patterns Using the Hasba Method
A. Thalal

2021

By its beauty and the symmetry of its patterns, Islamic geometric Pattern (IGP) art has always attracted the interest of scientists. These methods to make geometric patterns were analyzed and proposed by several author scientists. In this paper, we present a new method called the ‘Âark method’ to construct new geometric patterns by using the method called “Hasba” (measurement). That is widely adopted by Moroccan artisans. This proposed method, based on the concept of symmetry, allows building numerous patterns by systematic and dynamic processes. Symmetrical patterns are constructed from an asymmetric element called the ‘fundamental region’ by applying reflections and rotations. Compared to the classical ‘Ribbon method’ which will be explained later on, the proposed method is tolerant to construct more than 200 patterns with different visuals. This demonstrates the ability of the proposed method to construct various motifs and can easily be used in a softwere program, for an automat...

View PDFchevron_right

Related topics

  • python programming language
    • 580 California St., Suite 400
    San Francisco, CA, 94104
    © 2025 Academia. All rights reserved